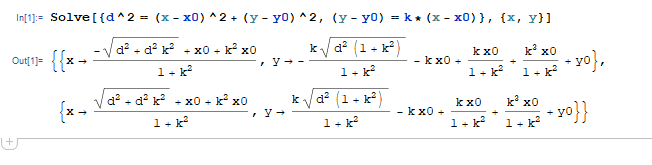两相交的直线段夹角平分的直线上过交点距离为d的另一点求解公式
两相交的直线段夹角平分的直线上过交点距离为d的另一点求解公式
问题描述：
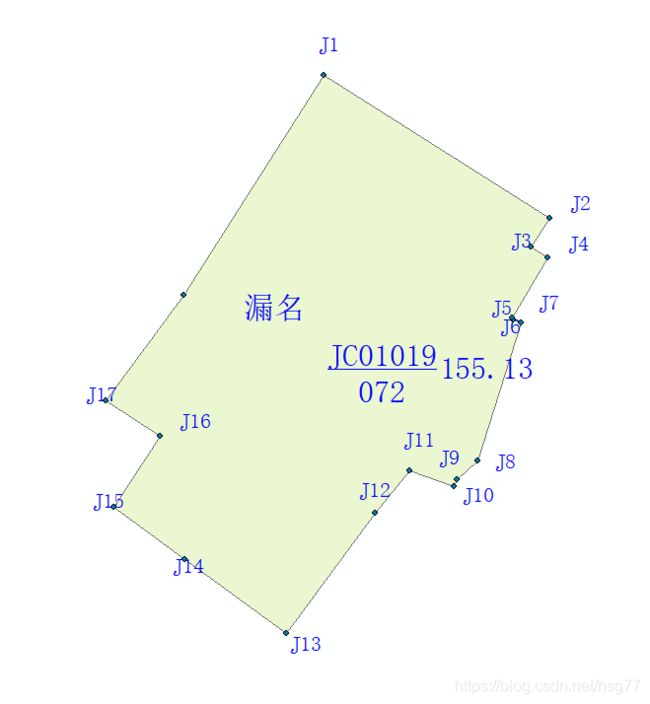
已知p0,p1,pN三个点，p0到p1走向直线段，pN到p0走向直线段，相交于p0点，
则pN到p0到p1夹角为a,平分夹角为a/2,求经过p0点方向角为平分线上距离p0点距离为d的点p(x,y）坐标值。
平分线点斜式方程为：
y-y0=k(x-x0)
两点距离公式为：
(y-y0)^2 +
（x-x0)^2
=d^2
斜率k=tg(a)
联合解方程组：
y-y0=k(x-x0)
(y-y0)^2 +
（x-x0)^2
=d^2
Mathematica 9 解公式表达式：
In[4]:= Solve[{d^2==(x-x0)^2+(y-y0)^2,(y-y0)==k*(x-x0)},{x,y}]
解结果：
文本公式：
In[4]:= Solve[{d^2==(x-x0)^2+(y-y0)^2,(y-y0)==k*(x-x0)},{x,y}]
2 2 2 2
-Sqrt[d + d k ] + x0 + k x0
Out[4]= {{x -> ------------------------------,
2
1 + k
2 2 3
k Sqrt[d (1 + k )] k x0 k x0
> y -> -(-------------------) - k x0 + ------ + ------ + y0},
2 2 2
1 + k 1 + k 1 + k
2 2 2 2 2 2 3
Sqrt[d + d k ] + x0 + k x0 k Sqrt[d (1 + k )] k x0 k x0
> {x -> -----------------------------, y -> ------------------- - k x0 + ------ + ------ + y0}}
2 2 2 2
1 + k 1 + k 1 + k 1 + k
In[5]:=
//创建界址点注记 宗地 如:J1,J2
private void createZJ_JZD_JX(ZHFeaturePolyLine from_zhFeat, IFeatureClass toFc)
{
IGeometry geo = from_zhFeat.pFeature.ShapeCopy;
if (geo != null && geo is IPolygon)
{
IPolygon pn = geo as IPolygon;
IPoint[] pointArray = zjTool.getPoints(pn).ToArray();
if (pointArray != null && pointArray.Length <= 2)
{ //跳过 不能构面的线
return;
}
string jNR = "";
IPoint p0 = null;
IPoint p1 = null;
IPoint pN = null;
//长度注记
for (int i = 0; i < pointArray.Length; i++)
{
//
int lastIndex = i + 1;
if (lastIndex >= pointArray.Length-1)
{
break;
}
if(i==0)
{
p0 = pointArray[i];
p1 = pointArray[i + 1];
pN= pointArray[pointArray.Length-2];
}
else if(i== pointArray.Length-2)
{
p0 = pointArray[i];
p1 = pointArray[0];
pN = pointArray[i - 3];
}
else
{
p0 = pointArray[i];
p1 = pointArray[i + 1];
pN = pointArray[i-1];
}
double A_P0_1 = zjTool.getAngleOfLine(p0, p1);
double A_PN_0= zjTool.getAngleOfLine(pN, p0);
double A_delta = zjTool.getAngleLine2Line(p0, pN, p1);// Math.Atan(Math.Abs(Math.Tan(A_PN_0) - Math.Tan(A_P0_1))/1+ Math.Tan(A_PN_0)* Math.Tan(A_P0_1));
double A_delta_2 = A_delta / 2.0;
//平分线方向角a
double A_lineMid = A_PN_0 + A_delta_2; //凸多边形
if(Math.Abs(A_PN_0- A_P0_1)<0.0001)
{
//三点共线 //凸多边形
}
else
{
double Area_delta = zjTool.getAreaLine2Line(p0, pN, p1);
if (Area_delta < 0)
{ //凹多边形
A_lineMid = A_PN_0 - A_delta_2;
}
}
//修正角度
if (A_lineMid>=360)
{
A_lineMid = A_lineMid - 360;
}
if (A_lineMid<0)
{
A_lineMid = A_lineMid + 360;
}
//
jNR = "J" + (i + 1).ToString();
//double newAngleZJ = zjTool.newAngleZJ(AofLine);
//获取注记文字长度
ITextSymbol txtSymbol = zjTool.getTestTextSymbol(this.zjFontName, this.zjFontSize);
double zj_width = zjTool.getTextSize(txtSymbol, jNR, true);
//获取注记起始点
IPoint zjPoint = zjTool.getZJPoint_JZP(p0, A_lineMid, this.zjDistance, zj_width);
double A_P0_Pzj = zjTool.getAngleOfLine(p0, zjPoint);
if (Math.Abs(A_lineMid - A_P0_Pzj) < 0.0001)
{ //注记方向与线走向一致
}
else
{ //注记方向与线走向 相反
zjPoint = zjTool.getZJPoint_JZP_1(p0, A_lineMid, this.zjDistance, zj_width);
}
//
this.writeZJPoint(zjPoint, jNR, 0, from_zhFeat, toFc);
this.writeZJPoint(zjPoint, ".", 0, from_zhFeat, toFc);
}
//
}
}
//-----
///
/// 根据余弦定理求两个线段夹角
///
/// 端点
/// start点
/// end点
/// public static IPolygon CreatePolygonNoSimplify(IPoint[] exteriorRingPoints, IPoint[][] interiorRingPoints)
{
IPolygon r = new PolygonClass();
IGeometryCollection geos = r as IGeometryCollection;
//添加外环
IPointCollection exRing = new RingClass();
for(int i=0;i< exteriorRingPoints.Length;i++)// (IPoint p in exteriorRingPoints)
{
IPoint p = exteriorRingPoints[i];
exRing.AddPoint(p);
}
geos.AddGeometry(exRing as IGeometry);
//如果有内环，添加内环
if (interiorRingPoints != null)
{
foreach (IPoint[] pc in interiorRingPoints)
{
IPointCollection inRing = new RingClass();
foreach (IPoint inP in pc)
inRing.AddPoint(inP);
geos.AddGeometry(inRing as IGeometry);
}
}
return r;
}