关于线性卡尔曼滤波的应用
大家晚上好,许久没有更新博客,心血来潮写一篇。今晚用力传感器的时候发现对采集的信号直接作微分的信号像被狗啃过一样。以前就了解过卡尔曼滤波,一直没有机会用,今晚花了点时间看了几篇csdn的博客然后实现了一下,推荐一下这个地址:
https://blog.csdn.net/revolver/article/details/37830675,里面的视频讲得很良心。
没时间排版,大家将就着看看。
数据下载
今晚在实验室采集了一段传感器的数据(emmm,有点失误地令每个数据都重复了一遍,所以前面几行matlab的代码会有点奇怪),我自己写了段代码实现一个简单的,只考虑了最简单的 f = f ˙ d t f=\dot{f}dt f=f˙dt这样的模型。
数据可以在这里下载:
链接:https://pan.baidu.com/s/16Yw_O4cudmhriKaLsUHzwg
提取码:bjmj
状态转移方程及参数选择
令:
f ( k ) = f ( k − 1 ) + f ˙ d t f ˙ ( k ) = f ˙ ( k − 1 ) f(k)=f(k-1)+\dot{f}dt\\ \dot{f}(k)=\dot{f}(k-1) f(k)=f(k−1)+f˙dtf˙(k)=f˙(k−1)
则有 X = [ f , f ˙ ] X=[f,\dot{f}] X=[f,f˙], A = [ 1 , d t ; 0 , 1 ] A =[1,dt;0,1] A=[1,dt;0,1], H = [ 1 , 0 ] H=[1,0] H=[1,0], U = 0 U=0 U=0;
X ( k ) = A X ( k − 1 ) Z ( k ) = H X ( k − 1 ) X(k) = AX(k-1)\\ Z(k)=HX(k-1) X(k)=AX(k−1)Z(k)=HX(k−1)
这样形式的动力学状态转移方程会在高频段部分出现一定的滞后,原因是我们认为速度不变,不过没办法啦,真实的模型并不是线性的,就目前我的水平还辨识不了,所以这个模型的精度比较差,我令过程噪声协方差矩阵 Q = [ 0 , 0 ; 0 , 0.015 ] Q=[0,0;0,0.015] Q=[0,0;0,0.015]。为了知道测量噪声协方差矩阵 R R R的取值,我先取了0~3s的力,这部分测量值的真实值是一个常量(因为我没有往力传感器加力),然后我取了它的方差,值在2.5e-4左右,比较小,因此我令 R = 1 e − 3 R=1e-3 R=1e−3.
实现公式
5条黄金公式如下:
X ( k ∣ k − 1 ) = A X ( k − 1 ∣ k − 1 ) + B U ( k ) − − − − − − − − − − − − − ( 1 ) P ( k ∣ k − 1 ) = A P ( k − 1 ∣ k − 1 ) A T + Q − − − − − − − − − − − − − − ( 2 ) X ( k ∣ k ) = X ( k ∣ k − 1 ) + K g ( Z ( k ) − H X ( k ∣ k − 1 ) ) − − − − − − − − − ( 3 ) K g = P ( k ∣ k − 1 ) ∗ H T ( H P ( k ∣ k − 1 ) H T + R ) − 1 − − − − − − − − − − ( 4 ) P ( k ∣ k ) = ( I − K g H ) P ( k ∣ k − 1 ) − − − − − − − − − − − − − − − − − ( 5 ) X(k|k-1)=AX(k-1|k-1)+BU(k) -------------(1)\\ P(k|k-1)=AP(k-1|k-1)A^T+Q--------------(2)\\ X(k|k)=X(k|k-1)+Kg(Z(k)-HX(k|k-1))---------(3)\\ Kg =P(k|k-1)*H^T(HP(k|k-1)H^T+R)^{-1}----------(4)\\ P(k|k) = (I-KgH)P(k|k-1)-----------------(5) X(k∣k−1)=AX(k−1∣k−1)+BU(k)−−−−−−−−−−−−−(1)P(k∣k−1)=AP(k−1∣k−1)AT+Q−−−−−−−−−−−−−−(2)X(k∣k)=X(k∣k−1)+Kg(Z(k)−HX(k∣k−1))−−−−−−−−−(3)Kg=P(k∣k−1)∗HT(HP(k∣k−1)HT+R)−1−−−−−−−−−−(4)P(k∣k)=(I−KgH)P(k∣k−1)−−−−−−−−−−−−−−−−−(5)
实现结果
matlab代码
forceTXT = load('forceSensorZ1.txt');
cut = 6000;
force = forceTXT(1:2:cut); HZ = 100;
dforce = [force(2:end); force(end)];
dforce = (dforce-force)*HZ;
t = (0:1:length(force)-1)/HZ;
figure(11);
subplot(211);
plot(t, force,'LineWidth',1.5); xlim([0, 3]);
subplot(212);
plot(t,dforce,'LineWidth',1.5); xlim([0, 3]);
dt = 0.01; % 10ms
Xk1k1 = [0 0]'; % 迭代估计初始值
Pk1k1 = [0 0; 0 0]; % 不确定性初始值
Kg = 0; % 卡尔曼增益初始值
% 估计力的状态方程,B = 0; U = 0;
% Xkk1 = AXk1k1 + Q
% Zkk1 = HXkk1 + R
A = [1 dt;
0 1 ];
Q = [0 0;
0 0.015]; % 过程噪声,影响的是状态变量的协方差
H = [1 0];
R = 1e-3; % 1e-3
logx = []; % 测量值
logx_ = []; % 估计值
logdx_ = []; % 估计值
logt = [];
for i=1:cut/2
logt = [logt i*dt];
Zk = force(i); % 当前时刻的测量值
% 状态方程
Xkk1 = A*Xk1k1; % (1)
Pkk1 = A*Pk1k1*A' + Q; % (2) , 上一时刻的最优估计值和这一时刻的估计值之间的协方差
% 结合观测方程的估计
Xkk = Xkk1 + Kg*(Zk - H*Xkk1); % (3) 最优估计值
Kg = Pkk1*H'/(H*Pkk1*H'+R);
Pkk = (eye(2)-Kg*H)*Pkk1;
% 下一轮的迭代参数更新
Xk1k1 = Xkk;
Pk1k1 = Pkk;
% 记录信号
logx = [logx Zk];
logx_ = [logx_ H*Xkk];
logdx_ = [logdx_ Xkk(2)];
end
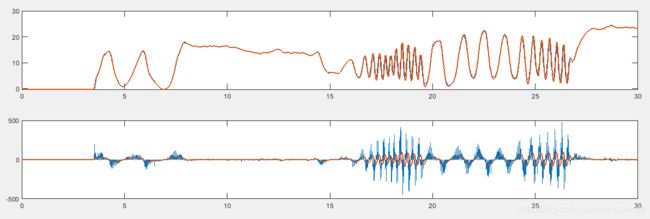
figure(34);
subplot(211);
plot(logt,logx); hold on;
plot(logt,logx_,'LineWidth',1.5); hold off;
subplot(212);
plot(logt,dforce); hold on;
plot(logt,logdx_, 'LineWidth',1.5); hold off;
2019年10月25日 凌晨2:11 广州天河