卷积神经网络学习路线（七）| 经典网络回顾之AlexNet

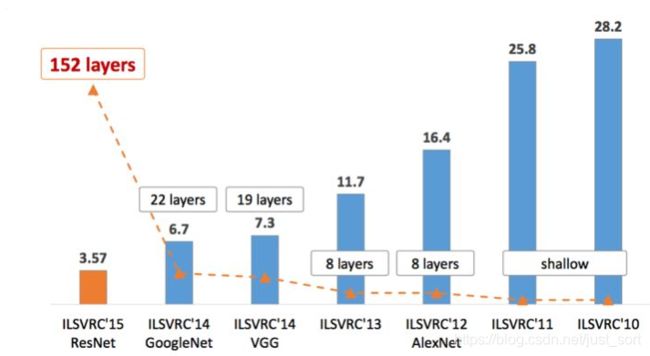开篇的这张图代表ILSVRC历年的Top-5错误率，我会按照以上经典网络出现的时间顺序对他们进行介绍，同时穿插一些其他的经典CNN网络。

前言

这是卷积神经网络学习路线的第七篇文章，主要回顾一下经典网络中的AlexNet。

背景

在卷积神经网络学习路线（六）中讲到了LeNet是第一个真正意义上的卷积神经网络，然后发明者Lecun也被称为卷积神经网络之父。但LeNet发明后的几十年时间，深度学习仍然处于低潮期，很少人去做研究。直到2012年AlexNet在ImageNet竞赛中以超过第二名10.9个百分点的绝对优势一举夺冠开始，深度学习和卷积神经网络一举成名。自此，深度学习的相关研究越来越多，一直火到了今天。

AlexNet的贡献

• 更深的网络
• ReLU激活函数
• Dropout
• LRN
• 数据增强

网络结构

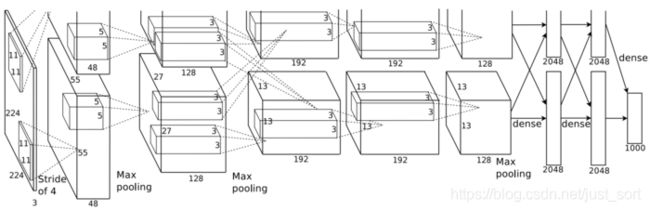
AlexNet的网络结构如下图所示：

从上图可以看到AlexNet一共包含$5$个卷积层和$3$全连接层，层数比LeNet多了不少，并且最后利用$1000$个神经元的全连接层输出$1000$个类别的概率。整个网络的输入规定为$256\times 256$，为了增强模型的泛化能力，避免过拟合的发生，论文使用了随机裁剪的方法将原始的$256\times 256$的图像随机裁剪，得到尺寸为$224\times 224\times 3$的图像，输入到网络训练。从上图还可以看到网络有两个分支，这是因为当时一块GPU的显存不够所以使用了两块GPU分别训练，同时在最后的全连接层进行特征融合得到最后的结果。接下来我们来分析一下网络中特征图的维度变化，以第一个分支为例：

• 数据输入，尺寸为$[224,224,3]$
• 第一个卷积层conv1的卷积核尺寸为$11\times 11$，滑动步长为$4$，卷积核数目为$48$。卷积后得到的输出矩阵维度为$[48,55,55]$。值得注意的是如果直接按照卷积的定义来计算的话，那么输出特征的长宽应该是$(224-11)/4+1$，这个值并不是$55$，因此这里的值是将原图做了padding之后再进行卷积得到的，具体来说就是将原图padding到$227\times 227$，这样再计算就是$(227-11)/4+1=55$了。所以这一层的输出特征图维度就是$[48,55,55]$。
• 第一个卷积层后面接一个激活函数ReLU层。处理后的特征图维度仍为$[48,55,55]$。
• 将经过激活函数处理的特征图通过一个LRN层。输出维度仍为$[48,55,55]$。
• 接下来是第一个池化层。使用的是Max Pooling池化操作，池化操作的池化核大小为$3\times 3$，步长为$2$，所以池化后的特征图尺寸为$(55-3)/2+1=27$。因此输出特征图维度为$[48,27,27]$。
• 第二个卷积层conv2输入为上一层的特征图，卷积核的个数为$128$个，注意这是第一个分支，第二个分支每层的结构和第一层完全一致，也就是说现在在显卡显存够的情况下可以直接设置第二个卷积层的通道数为$128\times 2=256$。卷积核的大小为$5\times 5$，$pad=2$，$stride=1$，同样也经过ReLU，LRN，然后再经过MaxPooling层，其中pool_size=（3,3）,stride=2。最后输出特征图维度为$[13,13,128]$。
• 第三个卷积层conv3输入为上一层的输出特征图，卷积核个数为$192$，卷积核尺寸为$3\times 3$，$pad=1$，没有做LRN和Max Pooling。
• 第四个卷积层输入为第三个卷积层的输出，卷积核个数为$192$，卷积核尺寸为$3\times 3$，$pad=1$，没有做LRN和Max Pooling。
• 第五个卷积层为第四个卷积层的输出，卷积核个数为$128$，卷积核尺寸为$3\times 3$，$pad=1$。然后接一个MaxPooling层，其中pool_size=（3,3）,stride=2。
• 第六，七，八层为全连接层，每一层的神经元个数是$2048$，最终输出softmax为$1000$，即ImageNet分类比赛中目标的种类数。全连接层中使用了ReLU和Dropout。

再提醒一次，这是以一个分支为例，实际上所有的通道数都需要倍增才是AlexNet实际的特征图通道数。

ReLU

AlexNet之前神经网络一般使用tanh或者sigmoid作为激活函数，sigmoid激活函数的表达式为：
$f(x)=\frac{1}{1+e^{-x}}$
tanh激活函数的表达式为：
$tanh(x)=\frac{sinhx}{coshx}=\frac{e^x-e^{-x}}{e^x+e^{-x}}$
这些激活函数在计算梯度的时候都比较慢，而AlexNet提出的ReLU表达式为：
$ReLU(x)=max(0,x)$
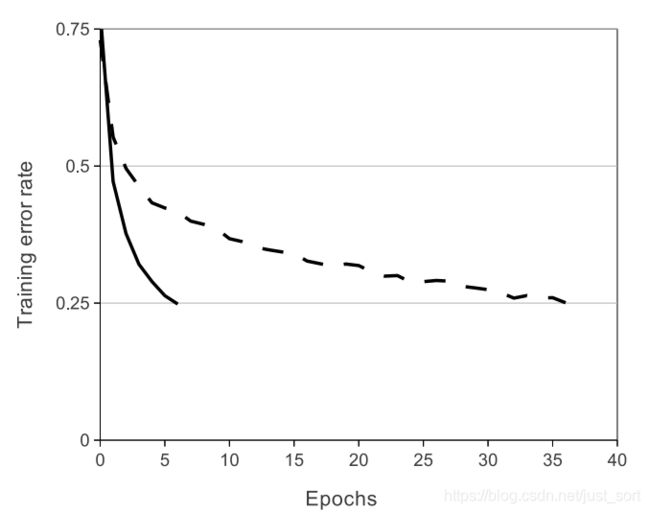
在计算梯度时非常快，下面这个图表示了分别使用ReLU和TanH作为激活函数的典型四层网络的在数据集CIFAR-10s实验中，错误率收敛到0.25时的收敛曲线，可以很明显的看到收敛速度的差距。虚线为TanH，实线是ReLU。

Local Response Normalization(局部响应归一化)

AlexNet中认为ReLU激活函数的值域没有一个固定的区间（sigmoid激活函数值域为(0,1)），所以需要对ReLU得到的结果进行归一化，这一点有点像之后的BN，都是改变中间特征图权重分布加速收敛。即论文提出的Local Response Normalization。局部响应归一化的计算公式如下：
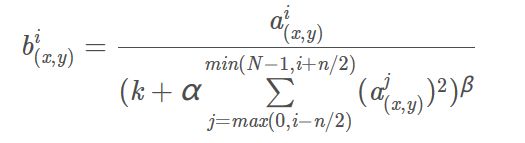其中，参数解释如下：

• i ：代表下标，即要计算的像素值的下标，从0开始开始算起。
• j ：代表平方累加索引，即从j~i的像素值平方求和。
• x,y：代表像素中的位置，公式中用不到。
• a：代表特征图里面i对应的像素值。
• N：每个特征图最内层向量的列数。
• k：超参数，由网络层中的blas指定。
• alpha：超参数，由网络层中的alpha指定。
• n/2：超参数，由网络层中的deepth_radius指定。
• beta：超参数，由网络层中的belta指定。

在网上找到一个生动的例子来说明这个层的作用，原始出处为：https://www.cnblogs.com/CJT-blog/p/9314134.html 。
即使用tensorflow来调用一下lrn层来观察一下参数变化，代码如下：

import tensorflow as tf  
  
a = tf.constant([  
    [[1.0, 2.0, 3.0, 4.0],  
     [5.0, 6.0, 7.0, 8.0],  
     [8.0, 7.0, 6.0, 5.0],  
     [4.0, 3.0, 2.0, 1.0]],  
    [[4.0, 3.0, 2.0, 1.0],  
     [8.0, 7.0, 6.0, 5.0],  
     [1.0, 2.0, 3.0, 4.0],  
     [5.0, 6.0, 7.0, 8.0]]  
])  
#reshape 1批次  2x2x8的feature map  
a = tf.reshape(a, [1, 2, 2, 8])  
  
normal_a=tf.nn.lrn(a,2,0,1,1)  
with tf.Session() as sess:  
    print("feature map:")  
    image = sess.run(a)  
    print (image)  
    print("normalized feature map:")  
    normal = sess.run(normal_a)  
    print (normal)

输出为：

feature map:  
    [[[[ 1.  2.  3.  4.  5.  6.  7.  8.]  
       [ 8.  7.  6.  5.  4.  3.  2.  1.]]  
      
      [[ 4.  3.  2.  1.  8.  7.  6.  5.]  
       [ 1.  2.  3.  4.  5.  6.  7.  8.]]]]  
    normalized feature map:  
    [[[[ 0.07142857  0.06666667  0.05454545  0.04444445  0.03703704  0.03157895  
         0.04022989  0.05369128]  
       [ 0.05369128  0.04022989  0.03157895  0.03703704  0.04444445  0.05454545  
         0.06666667  0.07142857]]  
      
      [[ 0.13793103  0.10000001  0.0212766   0.00787402  0.05194805  0.04  
         0.03448276  0.04545454]  
       [ 0.07142857  0.06666667  0.05454545  0.04444445  0.03703704  0.03157895  
         0.04022989  0.05369128]]]]

分析一下输出是怎么得到的？

由调用关系得出 n/2=2，k=0，α=1，β=1，N=8

第一行第一个数来说：i = 0,a = 1，min(N-1, i+n/2) = min(7, 2)=2，j = max(0, i - k)=max(0, 0)=0，下标从0~2个数平方求和，b=1/(1^2 + 2^2 + 3^2)=1/14 = 0.071428571

同理，第一行第四个数来说：i = 3，a = 4，min(N-1, i+n/2) = min(7, 5 )=5, j = max(0,1) = 1，下标从1~5进行平方求和，b = 4/(2^2 + 3^2 + 4^2 + 5^2 + 6^2) = 4/90=0.044444444

再来一个，第二行第一个数来说： i = 0，a = 8, min(N-1, i+n/2) = min(7, 2) = 2, j=max(0,0)=0, 下标从0~2的3个数平方求和，b = 8/(8^2 + 7^2 + 6^2)=8/149=0.053691275，其它的也是类似计算。

Dropout

Dropout原理类似于浅层学习算法的中集成算法，该方法通过让全连接层的神经元（该模型在前两个全连接层引入Dropout）以一定的概率失去活性（比如0.5）失活的神经元不再参与前向和反向传播，相当于约有一半的神经元不再起作用。在测试的时候，让所有神经元的输出乘0.5。当然在实际实现Dropout层的时候是在训练阶段所有Dropout保留下来的神经元的权值直接除以p，这样在测试过程中就不用额外操作了。Dropout的引用，有效缓解了模型的过拟合。关于为什么要除以p，以及Dropout实现细节由于比较复杂之后单独开一篇文章讲一讲。这个地方知道他可以降低过拟合的风险并且对准确率有提升就够了。

代码实现

# AlexNet
    def AlexNet(self):
        model = Sequential()
        # input_shape = (64,64, self.config.channles)
        input_shape = (self.config.normal_size, self.config.normal_size, self.config.channles)
        model.add(Convolution2D(96, (11, 11), input_shape=input_shape,strides=(4, 4),  padding='valid',activation='relu', kernel_initializer='uniform'))
        model.add(MaxPooling2D(pool_size=(3, 3), strides=(2, 2)))#26*26
        model.add(Convolution2D(256, (5, 5), strides=(1, 1), padding='same', activation='relu', kernel_initializer='uniform'))
        model.add(MaxPooling2D(pool_size=(3, 3), strides=(2, 2)))
        model.add(Convolution2D(384, (3, 3), strides=(1, 1), padding='same', activation='relu', kernel_initializer='uniform'))
        model.add(Convolution2D(384, (3, 3), strides=(1, 1), padding='same', activation='relu', kernel_initializer='uniform'))
        model.add(Convolution2D(256, (3, 3), strides=(1, 1), padding='same', activation='relu', kernel_initializer='uniform'))
        model.add(MaxPooling2D(pool_size=(2, 2), strides=(2, 2)))
        model.add(Flatten())
        model.add(Dense(4096, activation='relu'))
        model.add(Dropout(0.5))
        model.add(Dense(4096, activation='relu'))
        model.add(Dropout(0.5))
        model.add(Dense(self.config.classNumber, activation='softmax'))
        # model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
        return model

注意这一份代码中没有使用到LRN，如果想使用LRN可以自行加上，实际上AlexNet使用的LRN对准确率提升是比较有限的。可能更多好处是加速了网络收敛。

后记

这是卷积神经网络学习路线的第七篇文章，介绍了经典网络中的AlexNet，希望对大家有帮助。

卷积神经网络学习路线往期文章

卷积神经网络学习路线（一）| 卷积神经网络的组件以及卷积层是如何在图像中起作用的？

卷积神经网络学习路线（二）| 卷积层有哪些参数及常用卷积核类型盘点？

卷积神经网络学习路线（三）| 盘点不同类型的池化层、1*1卷积的作用和卷积核是否一定越大越好？

卷积神经网络学习路线（四）| 如何减少卷积层计算量，使用宽卷积的好处及转置卷积中的棋盘效应？

卷积神经网络学习路线（五）| 卷积神经网络参数设置，提高泛化能力？

卷积神经网络学习路线（六）| 经典网络回顾之LeNet

---

欢迎关注我的微信公众号GiantPandaCV，期待和你一起交流机器学习，深度学习，图像算法，优化技术，比赛及日常生活等。