A Fast Single Image Haze Removal Algorithm Using Color Attenuation Prior——基于颜色衰减先验单图片去雾算法原理...

       本人最近在研究去雾方面的最新文献（2016年初），当然去雾方面的经典论文是何凯明博士的《Single Image Haze Removal Using Dark Channel Prior》，我这里讲的论文主要是自己平时在看的一些文献，看的过程中进行总结，一方面是给自己看论文留下一点可参考的东西，另一方面希望能对各位产生帮助。可能有些地方不尽如人意，不喜勿喷。

一、专业词汇：

图1	图2
图3	图4

 

 

 

 

 

 

 

 

 

 

 

 

 

raw depth map：由雾图恢复过来的深度图，如图1所示

blocking artifacts:块效应，如图2所示

transmission maps：去雾要删掉的图，如图3所示

airlight：大气散射光

二、颜色衰减先验

这篇文章提出了一种新的先验——颜色衰减先验。首先讲讲什么是颜色衰减先验：

      

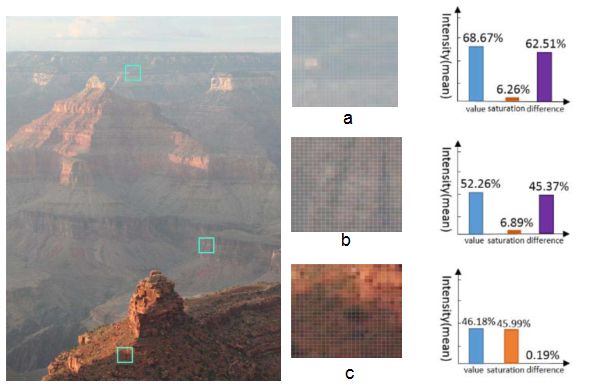
      通过对雾霾图的场景深度建模（线性模型），它是说图像的深度和亮度，饱和度之间存在线性关系。如上图所示，c区域为近景无雾部分，b区域远近适中，有一定雾，a区域为远景雾气浓重。由c右边图表可知，c图的亮度46.18%，饱和度很高，两者几乎没差。通过图表的比较可以得出以下几个结论：1.饱和度很容易受雾气的影响，一旦有一点雾，下降的很快。2.亮度在有雾的情况下（有散热光)反而会更亮。3.无雾情况下，亮度和饱和度几乎没差，受雾的影响下，亮度和饱和度之差悬殊。并且雾越浓重，两者相差越悬殊，也就是说亮度和饱和度之差和雾浓度正相关。

基于场景深度和雾浓度的关系，我们可以推出：

                                             深度和亮度与饱和度之差正相关！

     于是有 d(X)=θ₀+θ₁v(X)+θ₂s(X)+ε(X).

三、计算θ₀，θ_1,θ₂和σ²的值

d(X)=θ₀+θ₁v(X)+θ₂s(X)+ε(X)，

d是深度，v是亮度，s是饱和度。θ₀，θ₁，θ₂线性系数。ε(X)是随机变量表示模型的随机错误。可以把ε当做随机图。

我们让ε(X)~ N(0,σ²)，得d(X)-θ₀-θ₁v(X)-θ₂s(X)~N(0,σ²) ---->d(X)~N(θ₀+θ₁v+θ2s,σ²)

明确问题：亮度v，饱和度s已知，需要计算θ₀，θ₁，θ_2，σ的值，关键在于深度d目前不可测量于是有了以下方法。

　　a.合成图像数据集

     

　　因为测量图片的深度比较困难，没有量化的方法（即d未知）。受唐在<>文中的方法。根据大气散射模型：I(X) = J(X)t(X)+A(1-t(X)),t(X) = e^-βd(X)，β散射系数跟大气情况有关。本文采用：清晰无雾图 + 随机深度图 【服从（0,1）均匀分布】+随机大气光A= 样本雾图

第一，对每一张清晰图，我们都产生一张相同大小的随机深度图，合成深度图的像素值服从在开区间(0,1)的标准均匀分布，即A(1-t(X))。第二，产生0.85

     b.最大似然估计

对于联合概率密度函数，我们假设每个像素出错的概率是独立的，可得：

   

对该式做最大似然估计，两边同时取以e为底的log，然后化简对θ₀，θ₁，θ_2，σ分别做协方差求极值得：

根据公式(16)-(19),采用梯度下降算法去计算θ_0，θ_1，θ₂的值

 1 /*
 2 *Input: the training brightness vector v,the training saturation vector 
 3 *s,the training depth vector d,and the number of iteration t
 4 *Output:linear coefficients θ0，θ1，θ2，the variable σ2
 5 *Auxiliary functions:
 6 *   function for obtaining the size of the vector: n=size(in)
 7 *   function for calculating the square: out=square(in)
 8 */
 9 Begin
10     n=size(v);
11     θ0=0;θ1=1;θ2=-1;
12     sum=0;wSum=0;vSum=0;sSum=0;
13     for iteraiton from 1 to t do
14           for index from 1 to n do
15               temp=d[i]-θ0-θ1*v[i]-θ2*s[i];
16               wSum=wSum+temp;
17               vSum=vSum+v[i]*temp;
18               sSum=sSum+s[i]*temp;
19               sum=sum+square(temp);
20           end for
21     σ2=sum/n;
22     θ0=θ0+wSum;θ1=θ1+vSum;θ2=θ2+sSum;
23     end for
24 End    

 本文用了500个训练样本和1.2亿像素点训练线性模型。经过517代最后得出的最好系数θ0=0.121779,θ1=0.959710,θ2=-0.780245,σ=0.041337。确定了相关系数，我们就可以用来恢复有雾图的深度。

四、深度图恢复

b就是由a恢复的深度图，称为raw depth map.黑色景物比较近，白色比较远。图b就出现了"白鹅效应"，图中的白鹅本身是比较近的，但由于其本身就是白色，误认为是远景，这会影响结果的准确性。

                                       

我们取在以遍历的某像素x为中心的r*r图像区域内的最小值，结果如图c所示，有效解决但是出现了块效应。最后才经过导向滤波得到图d.

五、清晰图恢复

通过d，A和公式1，2恢复场景J。为了抑制噪声，t(X)选取0.1-0.9之间。--- ①
I(X) = J(X)t(X)+A(1-t(X)), --- ②
t(X) = e^-βd(X) --- ③
1、由②③可知在深度图中的白色区域深度无限深，所以I(X)=A,所以本文直接选取深度图中0.1%亮度像素，选取亮度最集中的一块作为大气光A。

2、由①②③得出公式：

有了该公式于是可以对J(X)无雾图进行恢复已达到目标结果。

散射系数β表示大气朝各个方向散射光的单位体积的能力。换句话说，间接决定了去雾的强度。

图11(e-g)不同β的transmission maps，(b-d)是相应去雾结果。可以看出，β太小去雾效果不好，而β太大则去雾过渡(图d变黑）。因此选取合适的β非常重要。大多数情况β=1.0去雾效果已经足够了。

 

转载于:https://www.cnblogs.com/zjuthantics/p/5276856.html