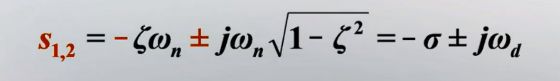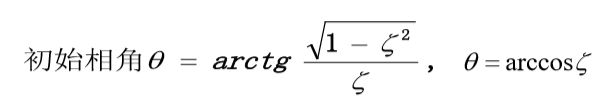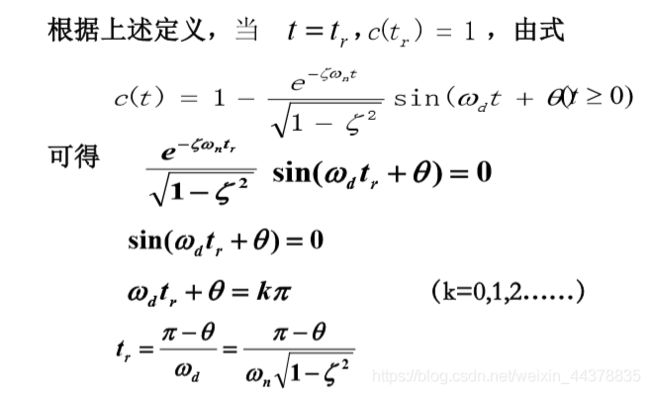(十)【自控原理】(线性系统的时域分析)二阶系统的时域响应
【自控原理专栏】
文章目录
- C 二阶系统的时域响应
- C.a 二阶系统的单位阶跃响应
- C.a.a 过阻尼( ζ \zeta ζ > 1 )的情况
- C.a.b 临界阻尼 ( ζ = 1 \zeta=1 ζ=1)的情况
- C.a.c欠阻尼( 0 < ζ < 1 0<\zeta<1 0<ζ<1)的情况
- C.a.d 无阻尼( ζ = 0 \zeta=0 ζ=0)的情况
- C.a.e 二阶系统响应情况总结
- C.b 二阶系统瞬态性能指标
- C.b.a 上升时间tr
- C.b.b 峰值时间 t p t_p tp
- C.b.c 超调量 σ \sigma σ
- C.b.d 调节时间 t s t_s ts
- C.b.e 振荡次数N
- C.c 二阶系统性能的改善
- C.c.a 速度反馈控制
- C.c.b 比例-微分控制
C 二阶系统的时域响应
什么是二阶系统?
以二阶微分方程作为运动方程的控制系统,称为二阶系统。
其结构图为:
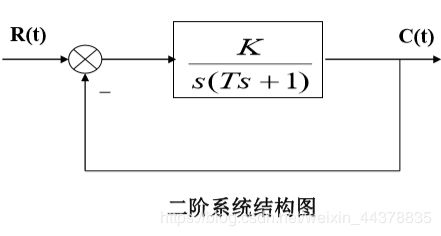
其中K为系统的开环放大系数, T为时间常数。
传递函数可以由梅逊公式或以下式子得到:
G H 1 + G H \frac{GH}{1+GH} 1+GHGH
系统的闭环传递函数为 :
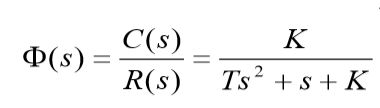
为了分析方便,将系统的传递函数改写成如下形式
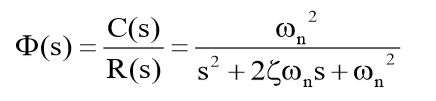
其中, ζ = 1 2 T K \zeta=\frac{1}{2\sqrt{TK}} ζ=2TK1称为阻尼比; w n = K T w_n=\sqrt{\frac{K}{T}} wn=TK称为无阻尼自然振荡角频率,(简称为无阻尼自振频率)
ζ \zeta ζ和 w n w_n wn是决定二阶系统动态特性的两个非常重要的参数,二阶系统的性能分析和描述,基本上是通过这两个体现其特征的结构参数来表示的。
系统的闭环特征方程为 :
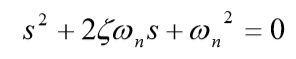
它的两个根为 :

二阶系统特征根(即闭环极点)的形式随着阻尼 比 ζ \zeta ζ取值的不同而不同。
C.a 二阶系统的单位阶跃响应
设系统的输入为单位阶跃函数,则 系统输出响应的拉氏变换表达式为 :
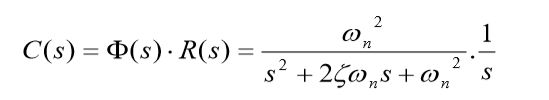
可以得到:
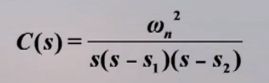
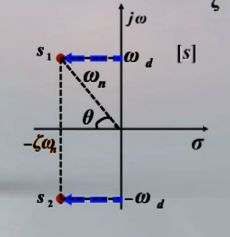
其中 s 1 , s 2 s_1,s_2 s1,s2是系统的闭环极点,因为当阻尼比 ζ \zeta ζ属于不同取值范围时,二阶系统的闭环极点在s平面上的位置就不同,其时间响应也对应地有不同的运动规律。
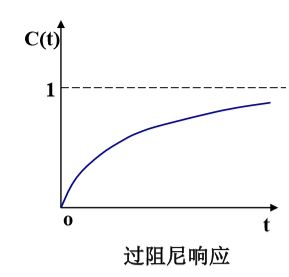
C.a.a 过阻尼( ζ \zeta ζ > 1 )的情况
系统具有两个不相等的负实数极点 :
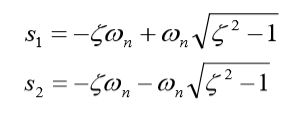
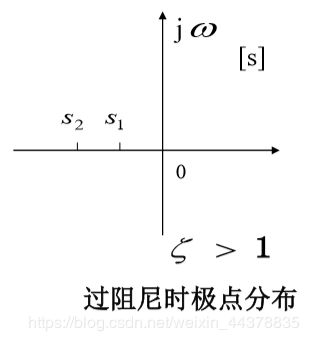
两个不相等的负实数对应于s平面负实轴上的两个不等实极点,此时称该系统为过阻尼系统
零初始条件下:
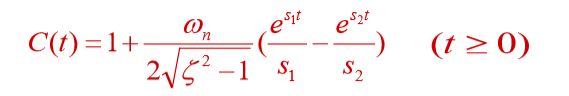
稳态分量为1,瞬态分量包含两个衰减指数项,曲线单调上升
- 单位阶跃响应曲线单调上升,既无超调,也无振荡。
- 单位阶跃响应的稳态分量与输入信号相同,因此无稳态误差

分析:当 ζ > > 1 \zeta>>1 ζ>>1时,由于极点 s 2 s_2 s2比 s 1 s_1 s1距虚轴远得多,故 e s 2 t e^{s_2t} es2t比 e s 1 t e^{s_1t} es1t衰减快的多,可将二阶系统近似成一阶系统来处理。
C.a.b 临界阻尼 ( ζ = 1 \zeta=1 ζ=1)的情况
s 1 , 2 = − w n ζ s_{1,2}=-w_n\zeta s1,2=−wnζ
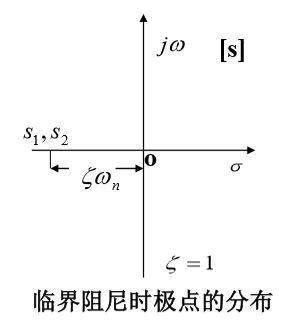
零初始条件下:


- 系统的输出响应无超调、无振荡,由零开始单调上 升,最后达到稳态值1,不存在稳态误差。
- ζ = 1 \zeta=1 ζ=1是输出响应的单调和振荡过程的分界,通常称为临界阻尼状态。
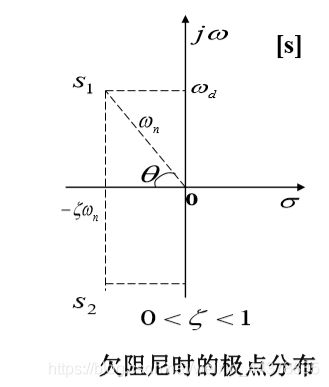
C.a.c欠阻尼( 0 < ζ < 1 0<\zeta<1 0<ζ<1)的情况
w d = w n 1 − ζ 2 w_d=w_n\sqrt{1-\zeta^2} wd=wn1−ζ2称为阻尼自振频率,此时该系统为欠阻尼系统。
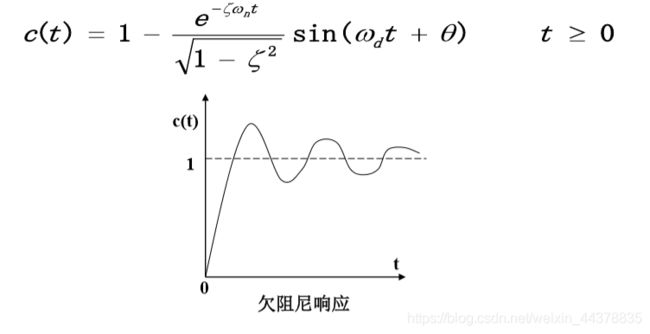
系统的稳态响应为1,瞬态分量是一个随时间t的增 大而衰减的正弦振荡过程。振荡的角频率为 w d w_d wd,它取决 于阻尼比 ζ \zeta ζ和无阻尼自然频率 w n w_n wn,若闭环极点远离实轴,则振荡频率大。衰减速度取决于 ζ w n \zeta w_n ζwn的大小,闭环极点远离虚轴,则衰减速度加快。此时系统工作在欠阻尼状态。输出响应 如图所示
C.a.d 无阻尼( ζ = 0 \zeta=0 ζ=0)的情况

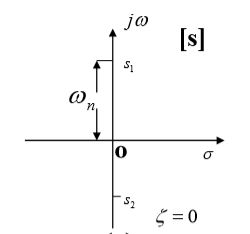
该系统为无阻尼系统。
零初始条件下:
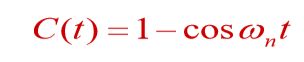
系统的输出响应是无阻尼的等幅振荡过程,其振荡频率为 w n w_n wn,而且响应曲线没有稳态,但又不发散,因此称为临界稳定。
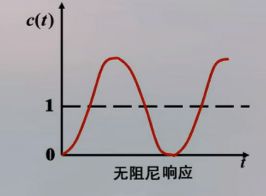
C.a.e 二阶系统响应情况总结

从振荡程度看, ζ \zeta ζ越小,响应特性振荡 得越厉害,随着 ζ \zeta ζ增大到一定程度,响 应特性变成单调上升。
从振荡程度看, ζ \zeta ζ越小,响应特性振荡 得越厉害,随着 ζ \zeta ζ增大到一定程度,响 应特性变成单调上升。
结论:随着 ζ \zeta ζ增大,振荡程度越来越小,过渡过程所需时间越长。综合考虑过渡过程 时间和振荡的程度,一般希望二阶系统工作在 ζ = 0.4 ~ 0.8 \zeta=0.4~0.8 ζ=0.4~0.8的欠阻尼状态,此时系统的过 渡过程时间比临界阻尼时更短,而且振荡特性也并不严重。 工程实际中,通常选取:

综上所述,不难看出频率 w n w_n wn和 w d w_d wd的物理意义。
w n w_n wn ——无阻尼自然振荡频率,此时系统输出为等幅振荡。
w d w_d wd——阻尼振荡频率。系统输出为衰减正弦振荡过程。

根据上面的分析可知,在不同的阻尼比时,二阶系统的响应具有不 同的特点。因此阻尼比 ζ \zeta ζ是二阶系统的重要特征参数。
若选取 w n t w_nt wnt为横坐标,可作出不同阻尼比时二阶系统单位阶跃响应曲线。
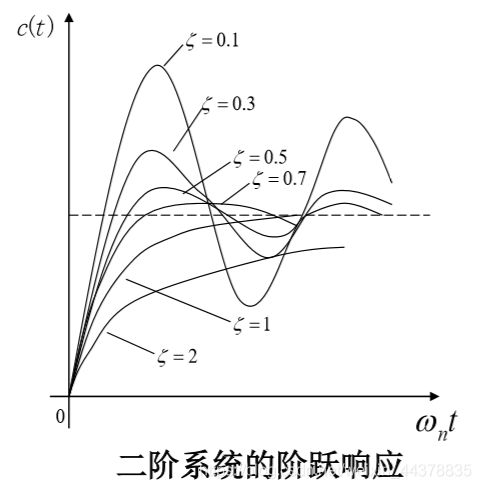
- ζ \zeta ζ越小,响应特性振荡得越厉害, 随着 ζ \zeta ζ增大到一定程度,响应特性变成单调上升的。
- 系统无振荡时,以临界阻尼时过 渡过程的时间最短,此时,系统 具有最快的响应速度。
- 系统在欠阻尼状态时,若阻尼比 在0.4~0.8之间,则系统的过渡 过程时间比临界阻尼时更短,此 时振荡特性也并不严重。
ζ 一般希望二阶系统工作在 ζ = 0.4 0.8 \zeta=0.4~0.8 ζ=0.4 0.8的欠阻尼状态下, 通常选取 ζ = 1 2 \zeta=\frac{1}{\sqrt{2}} ζ=21作为设计系统的依据。
C.b 二阶系统瞬态性能指标
系统在欠阻尼情况下的单位阶跃响应为
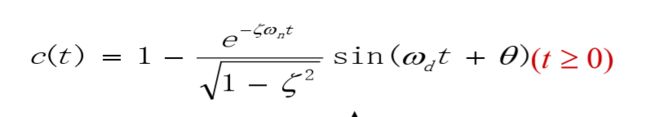
单位阶跃响应曲线:
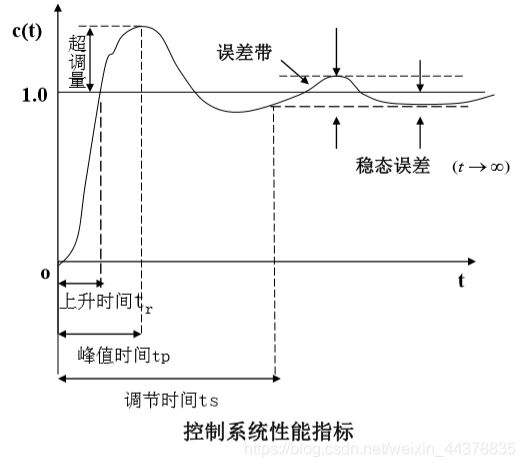
接下来将讨论以下关系:
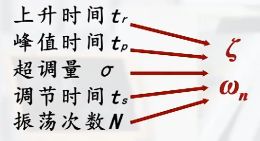
C.b.a 上升时间tr
响应曲线从零开始上升,第一次到达稳态值所需的时间,称为上升时间。
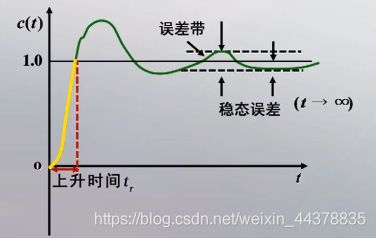
要使系统响应速度加快,必须减小 t r t_r tr,当阻尼比 ζ \zeta ζ一定时, w n w_n wn必须增大;若 w n w_n wn为固定值,则 ζ \zeta ζ越小, t r t_r tr也越小。
C.b.b 峰值时间 t p t_p tp
响应曲线C(t)从零开始到达第一个峰值所需时间,称为峰值时间。
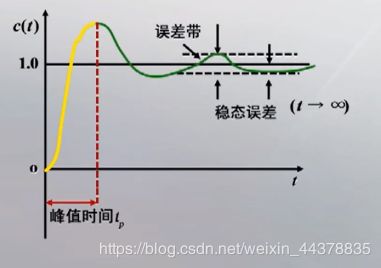
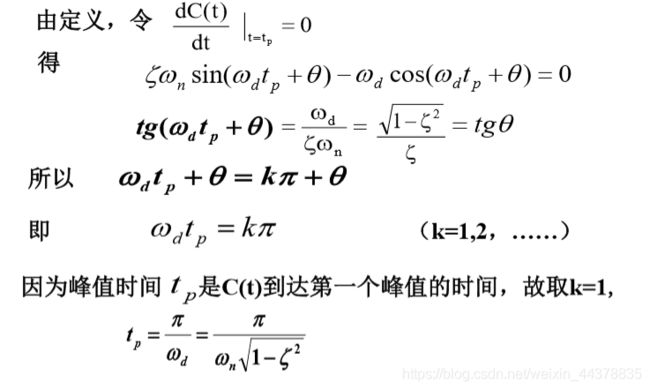
可见,当 阻尼比 ζ \zeta ζ一定时, w n w_n wn越大, t p t_p tp越小,反应速度越快。由于 w d w_d wd是闭环极点虚部的数值, w d w_d wd越大, 则闭环极点到实轴的距离越远,因此,也可以说峰值时间 t p t_p tp与闭环 极点到实轴的距离成反比。
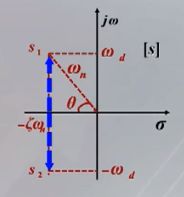
C.b.c 超调量 σ \sigma σ
在响应过程中,输出量C(t)超出其稳态值的最大差量与稳态值 之比称为超调量。

最大超调量Mp= σ ∣ c ( ∞ ) \sigma|_{c(\infty)} σ∣c(∞)
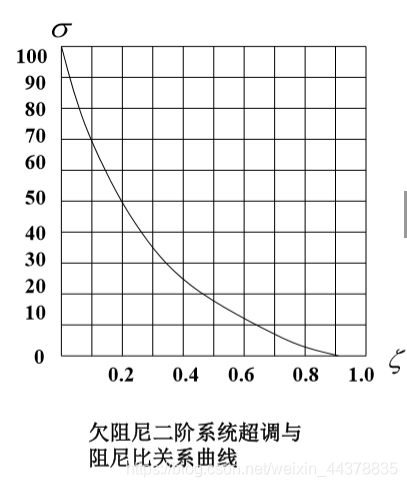
上式表明, σ \sigma σ只是 ζ \zeta ζ的函数,与 w n w_n wn无 关, ζ \zeta ζ越小 ,则 σ \sigma σ越大。当二阶系统的阻 尼比 ζ \zeta ζ确定后,即可求得对应的超调量 σ \sigma σ 。
C.b.d 调节时间 t s t_s ts
响应曲线到达并停留在稳态值的 ± 5 % \pm5\% ±5%(或 ± 2 % \pm2\% ±2% )误差范围内所 需的最小时间称为调节时间(或过渡过程时间)。

通常认为指数衰减到0.05或0.02时,过渡过程即结束
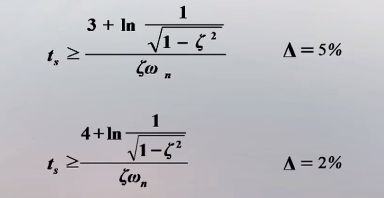
当 0 < ζ < 0.900 0<\zeta<0.900 0<ζ<0.900时,调节时间 t s t_s ts可以近似为:
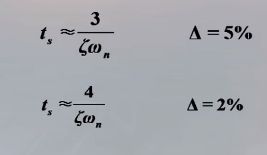
可以近似认为调节时间与闭环极点到虚轴的距离成反比。在设计系 统时, ζ \zeta ζ通常由要求的超调量所决定,而调节时间 t s t_s ts则由自然振 荡频率 w n w_n wn 所决定。即在不改变超调量的条件下,通过改变 w n w_n wn的值 可以改变调节时间。
C.b.e 振荡次数N
响应曲线在 0~ts时间内波动的次数称为振荡次数。

振荡次数只与阻尼比 ζ \zeta ζ有关。
结论:
阻尼比 ζ \zeta ζ和无阻尼自振频率 w n w_n wn是二阶系统两个重要特征参 数,它们对系统的性能具有决定性的影响。

C.c 二阶系统性能的改善
通过调整二阶系统的两个特征参数 ζ \zeta ζ和 w n w_n wn,可以改善系统的动态性能。
结论:
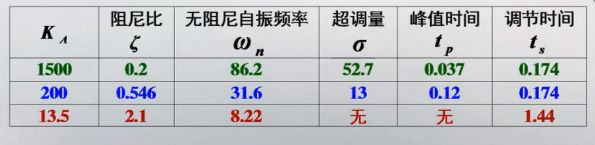
- K A K_A KA增大, σ \sigma σ增加, t p t_p tp减小, t r t_r tr不变(实部不变)。
- K A K_A KA减小, t p t_p tp增大, t r t_r tr增大,对于过阻尼时 t s t_s ts增大,没有超调。
表明KA增大可以提高响应初期的快速性,超调量也随之增加;
但仅靠调节放大器的增益,即比例调节,难以兼顾系统的快速性和平稳性。 要兼顾快速性和平稳性,需要采用校正装置。
改善二阶系统性能的方法:速度反馈控制和比例-微分控制
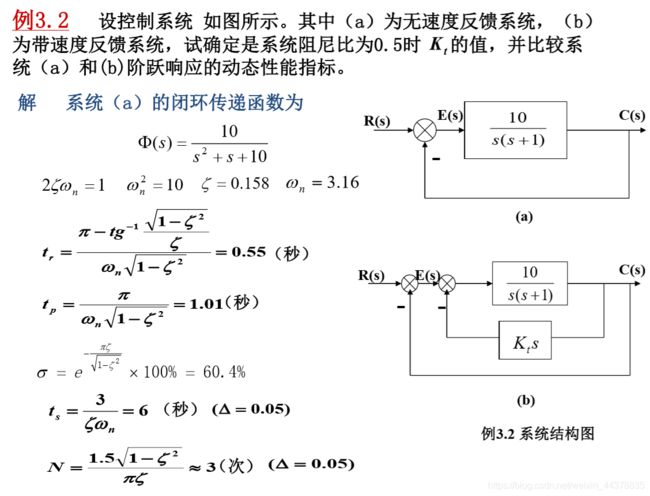
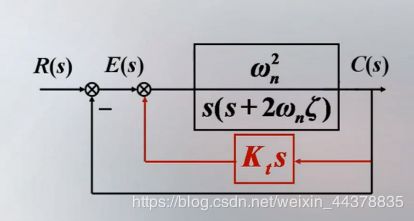
C.c.a 速度反馈控制
- w n ′ = w n , ζ ′ = ζ + 0.5 w n K t w_n'=w_n,\zeta'=\zeta+0.5w_nK_t wn′=wn,ζ′=ζ+0.5wnKt
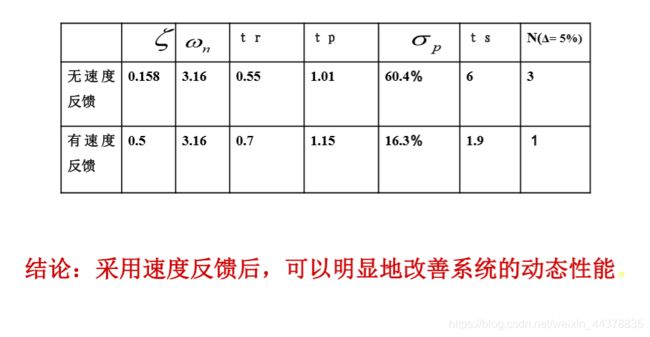
- 加入速度反馈后,自然振荡频率未改变,阻尼比增大,则超调量减小。
- 系统的调节时间减小,系统的响应速度得到提升。
C.c.b 比例-微分控制


通过与二阶系统的典型传递函数进行比较,我们可以发现:
1 可以通过适当选择微分时间常数 T d T_d Td,调整等效阻尼比 ζ ′ \zeta' ζ′的大小。
2 比例微分控制可以不改变自振频率 w n w_n wn,但可以增大系统的阻尼比,从而有效地抑制系统的振荡,减小超调量
3 系统虽然仍是二阶系统,但比典型的二阶系统多了一个零点(分子)。因此,比例微分控制的二阶系统又称为有零点的二阶系统。此时系统的性能指标无法直接应用在已建立的计算公式,需要通过输出响应来求解。
通过部分分式分解,这个有零点的二阶系统的单位阶跃响应 C ( s ) C(s) C(s)可以分为两个分量:

两项合成后系统的总响应 C ( s ) = C 1 ( s ) + 1 z s C 1 ( s ) C(s)=C_1(s)+\frac{1}{z}sC_1(s) C(s)=C1(s)+z1sC1(s)
其时域表达式为: c ( t ) = c 1 ( t ) + 1 z d c 1 ( t ) d t c(t)=c_1(t)+\frac{1}{z}\frac{dc_1(t)}{dt} c(t)=c1(t)+z1dtdc1(t)
上式第一项对应于典型二阶系统的时间响应,第二项为第一项的微分附加项。由于这个附加项的存在,增加了时间响应中的高次谐波分量,提高了系统响应的快速性。
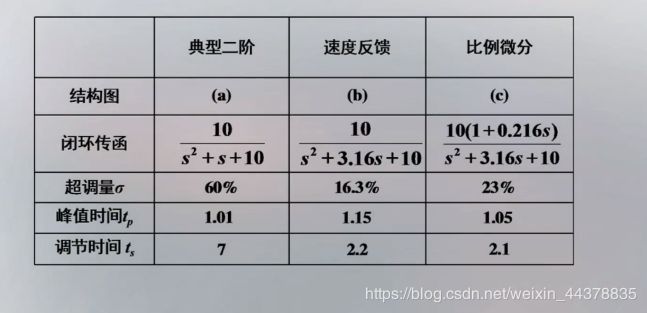
比例微分控制和速度反馈控制都可以改善系统的性能,提高系统的快速性,并适当降低超调量。接下来我们来讨论它们之间的差异:

k t = 0.216 k_t=0.216 kt=0.216分别写出各自的开环传函,闭环传函,并比较他们的动态性能。
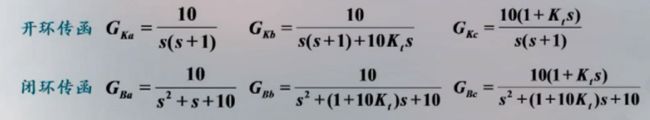
代入 k t k_t kt
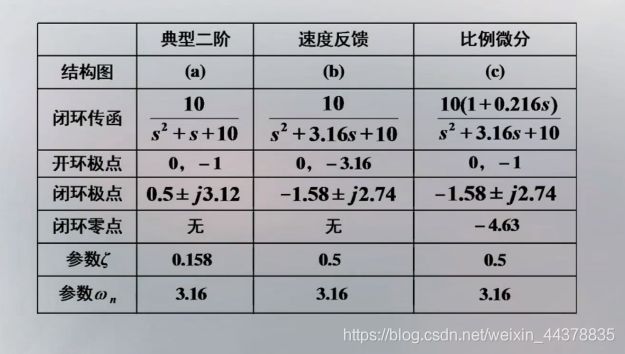
总结:
速度反馈通过改变系统闭环极点达到改善系统的目的,增大阻尼比从而减小超 调量;自然振荡频率不变从而减小调节时间。典型二阶和比例微分不能直接进行比较,因为不仅闭环传递函数发生变化,而且闭环零点也不同。可以将比例微分和速度反馈进行比较,区别是比例微分带有 一个闭环零点,- 闭环零点会使得系统的超调量增加,峰值时间减小,调节时间基本不变。