数据结构（C语言版） 第 八 章 排序 知识梳理 + 习题详解

本系列博客为《数据结构》（C语言版）的学习笔记（上课笔记），仅用于学习交流和自我复习

---

数据结构合集链接： 《数据结构》C语言版（严蔚敏版） 全书知识梳理（超详细清晰易懂）

内部排序,外部排序

若待排序记录都在内存中，称为内部排序；

若待排序记录一部分在内存，一部分在外存，则称为外部排序。

注：外部排序时，要将数据分批调入内存来排序，中间结果还要及时放入外存，显然外部排序要复杂得多。

一、归并排序

递归实现 - > 自上向下
非递归排序 - > 自下向上
时间复杂度：$O(NlogN)$

先分再合

/* 将序列对半拆分直到序列长度为1*/
void MergeSort_UptoDown(int *num, int start, int end)
{
    int mid = start + (end - start) / 2;
    if (start >= end)
        return;
    MergeSort_UptoDown(num, start, mid);
    MergeSort_UptoDown(num, mid + 1, end);
    Merge(num, start, mid, end);
}

void Merge(int *num, int start, int mid, int end)
{
    int *temp = (int *)malloc((end-start+1) * sizeof(int));    //申请空间来存放两个有序区归并后的临时区域
    int i = start;
    int j = mid + 1;
    int k = 0;
    while (i <= mid && j <= end)
        if (num[i] <= num[j])
            temp[k++] = num[i++];
        else
            temp[k++] = num[j++];
    while (i <= mid)
        temp[k++] = num[i++];
    while (j <= end)
        temp[k++] = num[j++];
    //将临时区域中排序后的元素，整合到原数组中
    for (i = 0; i < k; i++)
        num[start + i] = temp[i];
    free(temp);
}

二、交换排序

1.快速排序

基本思想：

任取一个元素 (如第一个) 为中心
所有比它小的元素一律前放，比它大的元素一律后放，形成左右两个子表；
对各子表重新选择中心元素并依此规则调整，直到每个子表的元素只剩一个

时间复杂度$O(NlogN)$

#include
using namespace std;
const int maxn=1000005;
int n,a[maxn];
void qsorts(int l,int r)
{
    int mid=a[(l+r)/2];
    int i=l,j=r;
    do{
        while(a[i]<mid)i++;
        while(a[j]>mid)j--;
        if(i<=j)
        {
            swap(a[i],a[j]);
            i++;
            j--;
        }
    }while(i<=j);
    if(j>l)qsorts(l,j);
    if(i<r)qsorts(i,r);
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    qsorts(1,n);
    for(int i=1;i<=n;i++)
        cout<<a[i]<<" ";
    cout<<endl;
}

2.冒泡排序

$O(N^2)$

void bubble_sort(int a[], int n)  
{
    int i,j,temp;    
    for (j=0;j<n-1;j++)    
    {                           
        for (i=0;i<n-1-j;i++)
        {
            if(a[i]>a[i+1])
            {
                temp=a[i];    
                a[i]=a[i+1];    
                a[i+1]=temp;
            }
        }
    }    
}

三、插入排序

每步将一个待排序的对象，按其关键码大小，插入到前面已经排好序的一组对象的适当位置上，直到对象全部插入为止。
即边插入边排序，保证子序列中随时都是排好序的

1.直接插入排序（基于顺序查找）

void insertSort(int* a,int T){
    int tmp,p;
    for(int i=1;i<T;i++){
        tmp=a[i];
        p=i-1;
        while(p>=0&&tmp<a[p]){
            a[p+1]=a[p];
            p--;
        }
        a[p+1]=tmp;
    }
}

2.折半插入排序（基于折半查找）

（1）基本思想

折半插入排序的基本思想是：顺序地把待排序的序列中的各个元素按其关键字的大小，通过折半查找插入到已排序的序列的适当位置。

（2）运行过程

直接插入排序的运作如下：

1、将待排序序列的第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。

2、从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置，在查找元素的适当位置时，采用了折半查找方法。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

void binary_insertion_sort(int arr[], int len) 
{
        int i, j, temp, m, low, high;
        for (i = 1; i < len; i++)
        {
               temp = arr[i];
               low = 0; high = i-1;
               while (low <= high)
               {
                      m = (low +high) / 2;
                      if(arr[m] > temp)
                               high = m-1;
                      else
                               low = m+1;
               }
         }
         for (j = i-1; j>=high+1; j--)
               arr[j+1] = arr[j];
         arr[j+1] = temp;
}

3.希尔排序（基于逐趟缩小增量）

#include 
#include 
void shellSort(int *a, int len)
{
    int i, j, k, tmp, gap;  // gap 为步长
    for (gap = len / 2; gap > 0; gap /= 2) {  // 步长初始化为数组长度的一半，每次遍历后步长减半,
    	for (i = 0; i < gap; ++i) { // 变量 i 为每次分组的第一个元素下标 
	        for (j = i + gap; j < len; j += gap) { //对步长为gap的元素进行直插排序，当gap为1时，就是直插排序
	            tmp = a[j];  // 备份a[i]的值
	            k = j - gap;  // j初始化为i的前一个元素（与i相差gap长度）
	            while (k >= 0 && a[k] > tmp) {
	                a[k + gap] = a[k]; // 将在a[i]前且比tmp的值大的元素向后移动一位
	                k -= gap;
	            }
	            a[k + gap] = tmp; 
	        }
	    }
    }
}
int main(void)
{
    int i, len, * a;
    printf("请输入要排的数的个数：");
    scanf("%d",&len);
    a = (int *)malloc(len * sizeof(int)); // 动态定义数组
    printf("请输入要排的数：\n");
    for (i = 0; i < len; i++) { // 数组值的输入
        scanf("%d",&a[i]);
    }   
    shellSort(a, len); // 调用希尔排序函数
    printf("希尔升序排列后结果为：\n");
    for (i = 0; i < len; i++) { // 排序后的结果的输出
        printf("%d\t",a[i]);
    }
    printf("\n");

    return 0;
}

四、选择排序

0.直接选择

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

void Selection_Sort(int Arr[])
	for (int i = 0; i < BUFFSIZE - 1; i++)
		for (int j = i + 1; j < BUFFSIZE; j++)
			if (Arr[i] < Arr[j])  // 将大的元素移到前面
			{
				int tmp = Arr[i];
				Arr[i] = Arr[j];
				Arr[j] = tmp;
			}
    //输出排序后的元素
	for (int i = 0; i < BUFFSIZE; i++)
		cout << Arr[i] << " ";
	cout << endl;
}

1.堆排序

一个序列，如果将序列看成一个完全二叉树，非终端结点的值均小于或大于左右子结点的值。

利用树的结构特征来描述堆，所以树只是作为堆的描述工具，堆实际是存放在线形空间中的。

• 首先堆是一颗完全二叉树
• 其次堆中存储的值是偏序

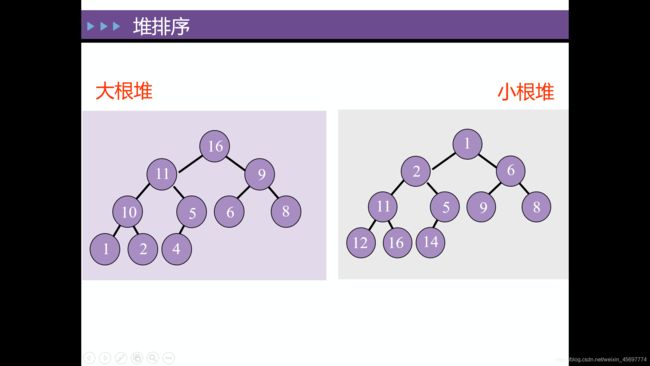
Min-heap(小根堆): 父节点的值小于或等于子节点的值

Max-heap(大根堆): 父节点的值大于或等于子节点的值

基本思路
将无序序列建成一个堆
输出堆顶的最小（大）值
使剩余的n-1个元素又调整成一个堆，则可得到n个元素的次小值
重复执行，得到一个有序序列

堆的重新调整

输出堆顶元素后，以堆中最后一个元素替代之
将根结点与左、右子树根结点比较，并与小者交换
重复直至叶子结点，得到新的堆

时间效率：$O(nlogn)$
空间效率：$O(1)$
稳 定 性：不稳定
适用于 $n$ 较大的情况

代码：

int heap[N],sz=0;
void push(int x)
{
    int i=sz++;
    while(i>0)//往上走
    {
        //父结点的编号
        int p=(i-1)/2;
        //如果不需要再交换就break;
        if(heap[p]<=x)break;
        heap[i]=head[p];
        i=p;
    }
    heap[i]=x;
}
//删除最小值：先把最小值丢掉，先把最后一个节点的值放到根节点处，然后排序交换即可
int pop()
{
    //最小值
    int ret=heap[0];
    int x=heap[--sz];
    int i=0;
    while(i*2+1<sz)//因为堆是完全二叉树偏左嘛
    {
        //左右儿子
        int a=i*2+1,b=i*2+2;
        //选出儿子中最小的
        if(b<sz&&heap[b]<heap[a])a=b;
        //如果不需要交换就break
        if(heap[a]>=x)break;
        //交换
        heap[i]=heap[a];
        i=a;
    }
    heap[i]=x;
    return ret;//返回被丢掉的那个最小值
}

2.二叉堆

二叉堆是一种支持插入、删除、查询最值的数据结构，是一棵满足堆性质的完全二叉树，树上的每一个节点都带有一个权值。

大根堆：
树上任意一个节点的权值都小于等于其父节点的权值。

小根堆：
树上任意一个节点的权值都大于等于其父节点的权值。

二叉堆的储存可以采用层次序列的储存方式，直接用一个数组保存：按从左到右，从上到下的顺序依次为二叉堆上的节点编号，如果根节点的编号为1的话，每个节点的左子节点的编号为根节点编号$\ast 2$，右子节点的编号为根结点编号$\ast 2+1$，每个节点的根节点的编号为自身编号 / 2。

以大根堆为例讨论二叉堆的常见操作：

二叉堆的插入操作：

将新插入的值放在储存二叉堆的数组的末尾，然后按照二叉堆的规则向上交换，直到满足二叉堆的性质，时间复杂度为二叉堆的深度，即：$\Theta (logN)$。

返回堆顶值：
大根堆堆顶的值为堆中的最大值，小根堆堆顶的值为堆中的最小值。

移除堆顶的值：
首先，将堆顶的值与数组末尾的节点交换，之后移除数组末尾的节点（在下面的样例中，移除节点通过记录节点个数的n−1n-1n−1来实现）；然后，将新的堆顶的值通过交换的方式向下调整，直至满足二叉堆的性质。

删除任意一个元素：
与删除对顶元素类似，将要删除的元素与数组末尾的元素交换，时候数组长度-1，然后分别检查是否需要向上或者向下调整，时间复杂度为$\Theta (logN)$。

二叉树的实现可以手写，也可以使用STL

3.手写二叉堆代码

int heap[MAX], n;

void up(int pos) // 向上调整
{
    while (pos > 1)
    {
        if (heap[pos] > heap[pos / 2])
        {
            swap(heap[pos], heap[pos / 2]);
            pos /= 2;
        }
        else
            break;
    }
}

void insert(int val) // 插入节点
{
    heap[++n] = val;
    up(n);
}

int top() // 返回堆顶元素
{
    return heap[1];
}

void down(int pos) // 向下调整
{
    int son = pos * 2;
    while (son <= n)
    {
        if (son < n && heap[son] <= heap[son + 1])
            son++; // 最大的子节点

        if (heap[pos] < heap[son])
        {
            swap(heap[pos], heap[son]);
            pos = son;
            son = pos * 2;
        }
        else
            break;
    }
}

void pop() // 弹出堆顶元素
{
    heap[1] = heap[n];
    n--;
    down(1);
}

void remove(int pos) // 删除指定位置的元素
{
    heap[pos] = heap[n];
    n--;
    up(pos);
    down(pos);
}

五、排序算法对比

反正我都直接$sort$ ( */ω＼*)

六、习题详解

1.下列排序算法中( )排序在一趟结束后不一定能选出一个元素放在其最终位置上。

A.冒泡
B.堆
C.归并
D.选择

答案： C

2.一组记录的关键码为（46，79，56，38，40，84），则利用快速排序的方法，以第一个记录为基准得到的一次划分结果为（ ）。

A. (40,38,46,79,56,84)

B.(40,38,46,56,79,84)

C.(38,40,46,56,79,84)

D.(40,38,46,84,56,79)

[解析] 本题主要考查的知识点是快速排序的方法。
[要点透析] 快速排序是对冒泡排序的一种改进。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小。
初始序列：46 79 56 38 40 84
第1次交换：40 79 56 38 46 84
第2次交换：40 46 56 38 79 84
第3次交换：40 38 56 46 79 84
第4次交换：40 38 46 56 79 84

3.下列排序算法中，在待排序数据已有序时，花费时间反而最多的是( )排序。

A.快速
B.希尔
C. 堆
D.冒泡

答案：A

4.下列排序算法中，占用辅助空间最多的是：( )

A.快速排序
B.归并排序
C.堆排序
D.希尔排序

答案:B

5.若用冒泡排序方法对序列{10,14,26,29,41,52}从大到小排序，需进行 （ ）次比较。

A.15
B.3
C.10
D.25

答案：A

6.下列内部排序算法中，在初始序列已基本有序（除去n个元素中的某k个元素后即呈有序，k<

A.简单选择排序
B.堆排序
C.直接插入排序
D.二路归并排序

答案：C

7.从未排序序列中挑选最大或最小元素,并将其依次放入已排序序列(初始时为空)的一端的方法,称为( )。

A.选择排序
B.冒泡排序
C.归并排序
D.插入排序

答案：A

七、第七章作业答案

二叉排序树或是空树，或是满足如下性质的二叉树：
若其左子树非空，则左子树上所有结点的值均小于根结点的值；
若其右子树非空，则右子树上所有结点的值均大于等于根结点的值；
其左右子树本身又各是一棵二叉排序树

从二叉搜索树的根结点一直沿右儿子向下找不一定能找到树中值最大的结点。
错

若二叉搜索树中关键码互不相同，则其中最小元素和最大元素一定是叶子结点。
错

当向二叉搜索树中插入一个结点，则该结点一定成为叶子结点。
对
折半查找可以在有序的顺序表或链表上进行查找。

错
二叉查找树的查找效率在 ( )时其查找效率最低。
A.结点太多
B.完全二叉树
C.结点太复杂
D.呈单枝树

答案：D

分别以下列序列构造二叉排序树，与用其他三个序列所构造的结果不同的是( )。

A．(100，80，90，60，120，110，130)
B．(100，120，110，130，80，60，90)
C．(100，60，80，90，120，110，130)
D．(100，80，60，90，120，130，110)

正确答案
C
答案解析
1．二叉排序树定义：二叉排序树是一棵二叉树，它或者为空，或者具有如下性质：1＞任一非终端结点若有左孩子，则该结点的关键字值大于其左孩子结点的关键字值；2＞任一非终端结点若有右孩子，则该结点的关键字值小于其右孩子结点的关键字值。是一种常用的动态查找表，上面首先给出了它的非递归形式。
二叉排序树也可以用递归的形式定义，即二叉排序树是一棵树，它或者为空，或者具有如下性质：1＞若它的左子树非空，则其左子树所有结点的关键字值均小于其根结点的关键字值；2＞若它的右子树非空，则其右子树所有结点的关键字值均大于其根结点的关键字值；3＞它的左右子树都是二叉排序树。
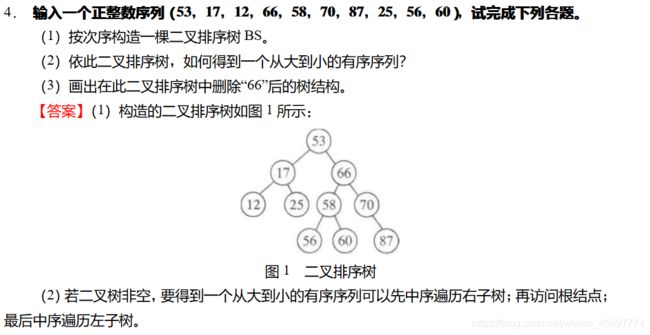
2．构造二叉排序树：一个无序序列可以通过构造一棵二叉排序树，然后再对这棵二叉树进行中序遍历，即可以变成有序序列。构造树的过程即为对无序序列进行排序的过程。例如：
设查找的关键字的序列为{45，24，53，45，12，90}，则生成二叉排序树的过程为：
[*]
特别说明：结点个数和取值都相同的表构成的二叉排序树树形可能不相同。其树形由结点的输入顺序决定。

设哈希表长为14，哈希函数是H(key)=key%11,表中已有数据的关键字为15，38，61，84共四个，现要将关键字为49的结点加到表中，用二次探测再散列法解决冲突，则放入的位置是( )

A.
5

B.
9

C.
3

D.
8

答案：
B
哈希表的平均查找长度( )。

A．与冲突处理方法有关而与表长无关
B．与冲突处理方法无关而与表长有关
C．与冲突处理方法和表长都有关
D．与冲突处理方法和表长都无关

正确答案
C
答案解析
[分析] 哈希表在查找过程中进行比较的关键字个数取决于哈希函数，处理冲突的方法和哈希表的装填因子，哈希表的装填因子标志哈希表的装满程度，与哈希表的长度有直接联系。

散列表的平均查找长度
A．与处理冲突方法有关而与表的长度无关
B．与处理冲突方法无关而与表的长度有关
C．与处理冲突方法有关而与表的长度有关
D．与处理冲突方法无关而与表的长度无关

A
问题有点含混，其实从根本上说，应该是既与冲突处理的方法有关，也与表的装填因子有关，只是与表的长度不直接相关

如果要求一个线性表既能较快地查找，又能适应动态变化的要求，则可采用的方法是( )。

A．分块法
B．顺序法
C．二分法
D．散列法

正确答案
A
答案解析
分块查找是将表分成若干块，分块的原则是数据元素的关键字在块与块之间是有序的，而块内元素的关键字是无序的。其可以适应动态变化的要求。其他3种是在顺序存储的一组记录内进行查找。

链接：https://www.nowcoder.com/questionTerminal/d40fef36fa484a27a5b4b895d469d91d?orderByHotValue=0&done=0&pos=153&mutiTagIds=584_585&onlyReference=false
来源：牛客网

设有一组记录的关键字为{19,14,23,1,68,20,84,27,55,11,10,79},用链地址法构造哈希表,哈希函数为H(key)=key
MOD 13,哈希地址为1的链中有()个记录

1
2
3
4

正确答案：D

链接：https://www.nowcoder.com/questionTerminal/d40fef36fa484a27a5b4b895d469d91d?orderByHotValue=0&done=0&pos=153&mutiTagIds=584_585&onlyReference=false
来源：牛客网

答案：D 4个
其实就是用关键字去套哈希函数为H(key)=key MOD 13,

19%13=6

14%13=1

23%13=10

1%13=1

68%13=3

20%13=7

84%13=6

27%13=1

55%13=3

11%13=11

10%13=10

79%13=1





  





就是14、1、27、79这四个数了。

关于杂凑查找说法不正确的有几个
(1)采用链地址法解决冲突时,查找一个元素的时间是相同的
(2)采用链地址法解决冲突时,若插入规定总是在链首,则插入任一个元素的时间相同的
(3)用链地址法解决冲突易引起聚集现象
(4)再哈希法不易产生聚集

1 在一条链的首还是尾上的数据需要的查找时间应该不同。
链地址法处理冲突简单，且无堆积现象，即非同义词决不会发生冲突，因此平均查找长度较短。3不对

顺序查找n个元素的顺序表，若查找成功，则比较关键字的次数最多为( )次。 (2分)
n
n+1
n+2
n-1

答案：n

假定有K个关键字互为同义词，若用线性探测再散列法把这K个关键字存入散列表中，至少要进行（）次探测。

A．K-1
B．K
C．K(K-1)/2
D．K(K+1)/2

正确答案
D
答案解析
[解析] 哈希涉及到构造哈希函数和处理)中突。解决冲突就是为出现冲突的关键字找到另一个”空”的哈希地址。开放地址法是常用的一种方法。
开放地址法：Hi=(H(key)+di)%m i=1，2，…k(km-1)，其中H(key)为哈希函数；m为哈希表表长；di为增量序列，当di1，2，3，…，m-1时，称为线性探测再散列。
用线性探测再散列法把这K个关键字存入散列表中，第1个关键字最少需进行1次探测，第2个关键字最少需进行2次探测，…第A个关键字最少需进行七次探测，所以最少要进行K(K+1)/2次探测。

在顺序表（8,11,15,19,25,26,30,33,42,48,50）中，用二分（折半）法查找关键码值20，需做的关键码比较次数为1。

8 11 15 19 25 26 30 33 42
48 50

0 1 2 3 4 5 6
7 8 9 10
假设低下标用low表示，高下标用high表示。
查找20：
开始low = 0, high = 10

mid=(low+high)/2

if mid==num
return ;
if mid>num
high = mid-1;
if mid low = mid +1;
第一次查找，找到中心的下标为(0+10)/2 =
5，即26，由于20小于26，所以，调整low = 0，high = 4
第二次查找，找到中心的下标为(0+4)/2 =
2，即15，由于15小于20，所以，调整low = 3，high = 4
第三次查找，找到中心的下标为(3+4)/2 =
3.5，向下取整取3，即19，由于19小于20，所以，调整low = 4，high = 4
第四次查找，找到中心的下标为4，不是20

在散列存储中，装填因子α的值越大，则( )。 (2分)
存取元素时发生冲突的可能性就越大
存取元素时发生冲突的可能性就越小
存取元素时不可能发生冲突
毫无影响

答案：A
装填因子越大，冲突可能性越大，
装填因子越小，冲突可能性就越小