剑指Offer刷题小结--一(1~6)

目录

1. 第一题：二维数组中的查找
2. 第二题：替换空格
3. 第三题：从尾到头打印链表
4. 第四题：重建二叉树
5. 第五题：用两个栈实现队列
6. 第六题：旋转数组的最小数字

---

第一题：二维数组的查找

题目链接

解析

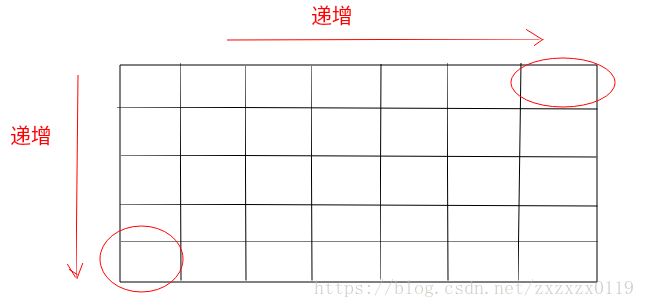
• 这个题目比较好的解题思路是从右上角或者左下角开始找；这个是 题目给定的每一行从左到右递增和每一列从上到下递增的原因；
• 例如，从右上角开始找，设置两个变量row，col分别代表列和行， 如果要找的数就是target，则直接返回；
• 如果arr[row][col] < target，那row = row + 1，因为它左边的都会arr[row][col]小，这是因为列增加的性质；
• 如果arr[row][col] > target，那 col = col - 1，因为它下面的都会arr[row][col]大，这是因为行增加的性质；
  

public class Solution {
    public boolean Find(int target, int [][] array) {
        int row = 0,col = array[0].length-1;
        while(row < array.length && col >= 0){
            if(array[row][col] == target){
                return true;
            }else if(array[row][col] > target){
                col--;
            }else {
                row++;
            }
        }
        return false;
    }
}

public class Solution {
    public boolean Find(int target, int [][] array) {
        int row = array.length - 1,col = 0;
        while(row >= 0 && col < array[0].length){
            if(array[row][col] == target){
                return true;
            }else if(array[row][col] > target){
                row--;
            }else {
                col++;
            }
        }
        return false;
    }
}

第二题：替换空格

题目链接

解析：

解析:

• 这个题目如果只是简单的插入的话，插入之后导致后面的元素的移动导致 需要O(n²)的复杂度；
• 这个的解决方法使用两个指针，可以达到O(n)复杂度；
• 首先计算出空格的个数，这样求的新的字符串的长度；
• 然后使用两个指针,新的指针second指向新的字符串的末尾，老指针first指向原来字符串的末尾，每次检查字符串的末尾如果是空格的话，就添加%20进去，否则把原来的字符串复制到后面；

public class Solution {
    public String replaceSpace(StringBuffer str) {
        int spaceNum = 0; //计算空格数量
        for(int i = 0; i < str.length(); i++)
            if(str.charAt(i) == ' ')
                spaceNum++;
        int first = str.length() - 1; //第一个指针
        int second  = str.length() + 2*spaceNum - 1; //第二个指针的位置
        str.setLength(second + 1); //新的长度 = oldLen + 2 * spaceNum
        
        while(first >= 0){
            if(str.charAt(first) == ' '){
                str.setCharAt(second--,'0');
                str.setCharAt(second--,'2');
                str.setCharAt(second--,'%');
            }else {
                str.setCharAt(second--,str.charAt(first));
            }
            first--;
        }
        return str.toString();
    }
}

---

第三题：从尾到头打印链表

题目链接

解析：

这个题目比较简单，可以用栈倒序，也可以递归，代码如下：

import java.util.ArrayList;
import java.util.Stack;
public class Solution {
    public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
        Stack<Integer>stack = new Stack<>();
        ListNode cur = listNode;
        while(cur != null){
            stack.push(cur.val);
            cur = cur.next;
        }
        ArrayList<Integer>res = new ArrayList<>();
        while(!stack.isEmpty()){
            res.add(stack.pop());
        }
        return res;
    }
}

import java.util.ArrayList;
import java.util.Stack;
public class Solution {
    //方法二
    public ArrayList<Integer> printListFromTailToHead(ListNode listNode) { 
	    ArrayList<Integer>res = new ArrayList<>();
        process(listNode,res);
        return res;
    }
     
    public void process(ListNode node,ArrayList<Integer>res){
        if(node == null)
            return;
        process(node.next,res);//先把next的存好
        res.add(node.val);//再存自己的
     }
}

---

第四题：重建二叉树

题目链接

解析：

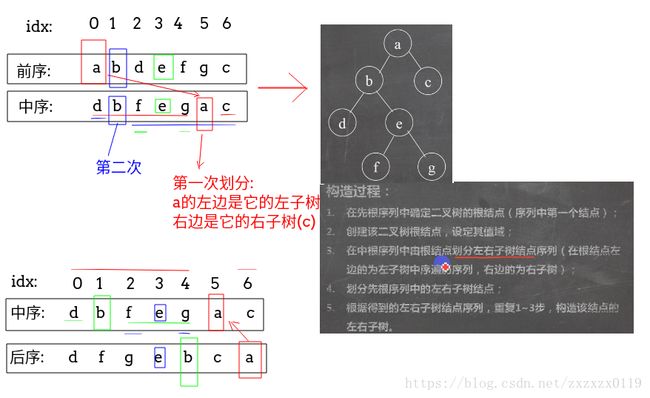
• 对于二叉树的建树问题，都是先建立根节点，然后 建立左子树，右子树，根据前序遍历和中序遍历，中序遍历和后续遍历都可以建立一颗二叉树，但是根据前序遍历和后续遍历不可以确定一颗二叉树，前序和后续在本质上都只是将子节点和父节点分离，没有指明左右子树的能力。

• 根据前序和中序建树时，前序遍历的第一个结点就是根，在中序遍历中找到根所在的位置，计算左边的长度，即为左子树的长度，然后计算出右子树的长度 = 总长度-左子树长度-1，然后递归建立左子树和右子树即可，代码如下(顺便贴上根据中序和后续遍历建树的代码)：

	 //根据前序和中序
    public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
        return process(pre, 0, pre.length - 1, in, 0, in.length - 1);
    }

    public TreeNode process(int[] pre, int pL, int pR, int[] in, int iL, int iR) {
        if (pL > pR || iL > iR) return null; //已经访问到null
        TreeNode root = new TreeNode(pre[pL]);
        int lLen = 0; //左子树    数组长度
        for (int i = iL; i <= iR && in[i] != pre[pL]; i++, lLen++) ;
        root.left = process(pre, pL + 1, pL + lLen, in, iL, iL + lLen - 1);
        root.right = process(pre, pL + lLen + 1, pR, in, iL + lLen + 1, iR); //记得是从终点是preright,和inright
        return root;
    }
    
    //根据中序和后序
    public TreeNode reConstructBinaryTreeByInPost(int[] in, int[] post) {
        return pro(in, 0, in.length - 1, post, 0, post.length - 1);
    }

    public TreeNode pro(int[] in, int iL, int iR, int[] post, int poL, int poR) {
        if (iL > iR || poL > poR) return null;
        TreeNode root = new TreeNode(post[poR]);
        int lLen = 0;    //左子树长度
        for (int i = iL; i <= iR && in[i] != post[poR]; i++, lLen++) ;
        root.left = pro(in, iL, iL + lLen - 1, post, poL, poL + lLen - 1);
        root.right = pro(in, iL + lLen + 1, iR, post, poL + lLen, poR - 1);
        return root;
    }

---

第五题：两个栈实现一个队列

题目链接

解析：

这个题目也比较简单，用两个栈直接模拟即可，两种思路，代码如下：

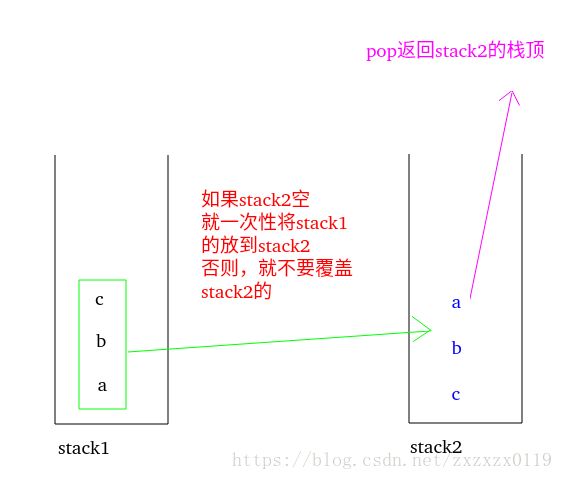
• 思路一: push的时候直接放到stack1；为了pop的操作，当stack2空(必须当stack2为空)的时候，一次性(必须一次性)要将stack1的全部push到stack2中，然后出队列的时候，取的就是stack2的栈顶；
  

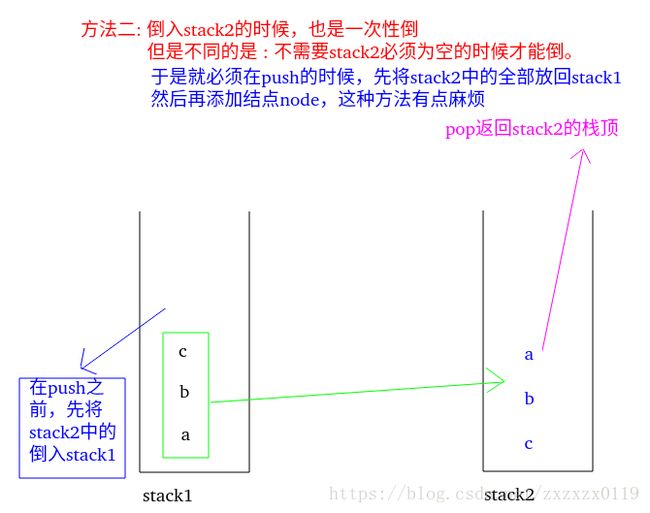
• 思路二: 思路一有一个条件就是必须当stack2为空的时候才能一次性将所有的stack1中的元素全部倒入stack2，而思路二不需要这样，但是为了满足这样，在push的时候，必须先将stack2中的所有元素先倒回stack1，然后再push；
  

思路一代码:

import java.util.Stack;
public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();
    
    public void push(int node) {
        stack1.push(node);
    }
    
    public int pop() {
        if(stack1.isEmpty() && stack2.isEmpty())
            throw new RuntimeException("Queue is empty!");
        if(stack2.isEmpty()){//如果stack2不空的话，就先不要将stack1的内容放进去
            while(!stack1.isEmpty())
                stack2.push(stack1.pop());
        }
        return stack2.pop();
    }
}

思路二代码:

import java.util.Stack;
public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();
    
    public void push(int node) {
        while(!stack2.isEmpty())
            stack1.push(stack2.pop());
        stack1.push(node);
    }
    
    public int pop() {
        if(stack1.isEmpty() && stack2.isEmpty())
            throw new RuntimeException("Queue is Empty!");
        while(!stack1.isEmpty())
            stack2.push(stack1.pop());
        return stack2.pop();
    }
}

---

第六题：旋转数组的最小数字

题目链接

解析

首先:

• 旋转之后的数组实际上可以划分成两个有序的子数组；
• 前面子数组的大小都大于后面子数组中的元素；

如果先解决没有重复元素的问题，这个问题会简单一些(这个题目可以有重复的元素)。
思路：

• 我们用两个指针L,R分别指向每次判断的数组左右边界。按照题目的旋转的规则，左边界应该是大于右边界的（没有重复的元素）。
• 然后找到数组的中间元素arr[mid]，arr[mid] > arr[L]，则中间元素位于前面的递增子数组，此时最小元素位于中间元素的后面。我们可以让第一个指针L 指向中间元素；(移动之后，第一个指针仍然位于前面的递增数组中)；
• arr[mid] < arr[L]，中间元素小于第一个元素，则中间元素位于后面的递增子数组，此时最小元素位于中间元素的前面。我们可以让第二个指针L 指向中间元素；(移动之后，第二个指针仍然位于后面的递增数组中)；
• 按照以上思路，第一个指针L总是指向前面递增数组的元素，第二个指针R总是指向后面递增的数组元素；
• 最终第一个指针L将指向前面数组的最后一个元素，第二个指针R指向后面数组中的第一个元素；
• 也就是说他们将指向两个相邻的元素，而第二个指针指向的刚好是最小的元素，这就是循环的结束条件；

以上思路解决了没有重复数字的情况，这一道题目添加上了这一要求，有了重复数字。
因此这一道题目比上一道题目多了些特殊情况：
我们看一组例子：｛1，0，1，1，1｝和 ｛1，1， 1，0，1｝都可以看成是递增排序数组｛0，1，1，1，1｝的旋转。
这种情况下我们无法继续用上一道题目的解法，去解决这道题目。因为在这两个数组中，第一个数字，最后一个数字，中间数字都是1。

第一种情况下，中间数字位于后面的子数组，第二种情况，中间数字位于前面的子数组。

因此当两个指针指向的数字和中间数字相同的时候，我们无法确定中间数字1是属于前面的子数组(绿色表示)还是属于后面的子数组（紫色表示）。

public class Solution {
    public int minNumberInRotateArray(int[] array) {
        if (array.length == 0)
            return 0;
        for (int i = 1; i < array.length; i++) {
            if (array[i] < array[i - 1])
                return array[i];
        }
        return array[0];
    }
}

public class Solution {
      public int minNumberInRotateArray(int[] array) {
        if(array.length == 0)
            return 0;
        int l = 0,r = array.length - 1;
        while(array[l] >= array[r]) {   // 确保是旋转的
            if(r - l == 1)//递归条件 l 是前一个递增序列的最后一个元素,r是后一个递增序列的第一个元素
                return array[r];
            int mid = l + (r-l)/2;
            if(array[l] == array[mid] && array[mid] == array[r]) {  //无法确定中间元素是属于前面还是后面的递增子数组
                for(int i = l+1; i <= r; i++)
                    if(array[i] < array[i-1])
                        return array[i];
            }
            //中间元素位于前面的递增子数组    ---> 此时最小元素位于中间元素的后面
            if(array[mid] >= array[l]) //注意我们这里认为 = 也算是上升的吧
                l = mid;  // not mid - 1
            else       // 中间元素位于后面的递增子数组     --->  此时最小元素位于中间元素的前面 
                r = mid;  // not mid + 1
        }
        return array[l];  // array[r] > array[l], directly return the array[l]
    }
}