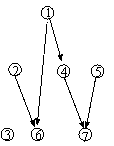快速最优通道布线算法(详细)
吴祖增,复旦大学电子工程系
说明:这是上世纪82年为昆明召开的全国CAD会议提供的一篇稿件,其详细内容从未在刊物上发表过,由于当时供稿是油印材料,布线插图均由学校出版社按照PDP/11-34机的输出图形用人工刻画出来,十分费工但仍极粗糙,且图、文均有不少遗漏和错误,未经审查就匆匆提供给会议使用(当然,即使查到问题,图的错误大部分已无法补救。)供稿份数也很少(仅100份),所以很想纠错和补漏后重新发表,但因原文手稿未找到,一直未能着手工作。最近找到了一份油印稿,所以就开始对文进行纠错和补漏,并用计算机直接屏幕输出图形代替人工刻图。由于字数远远超过5000,已无刊物容许刊登,所以用单行本发表。由于本文较长,为有利于阅读,我在前面添加了摘要、关键字和目录。又,运行结果比较表中有一项时间参数缺,因PDP/11机现早已淘汰,已无法再试验获得,为尊重历史,故仍让其为空。
【摘要】本文提出的快速最优通道布线算法是Kernighan-Schweikert-Deutche最优通道布线算法[ 2]和Wada最优曲干通道布线算法 [ 4]的改进,这些算法的“最优性”意义完全相同,但新算法执行速度比原有算法远远为快,一般情况下统计地可相差几倍、十几倍到几十倍,极端情况下则可相差更多数量级。
【关键字】通道,双层直干通道布线,垂直约束,约束环,水平重叠与重叠区,通道密度,静态与动态界限,分支限界方法,Kernighan-Schweikert-Deutche最优通道布线算法,Wada最优曲干通道布线算法,Deutche困难问题。
目 录
引言 ………………………………………..…………….…….. 1
基本概念 …………………………………..…………….…….. 2
前人结果回顾 ……………………..…………………….…….. 8
快速最优通道布线的思想与实现..………..…………….…….. 9
各种算法运行结果比较 …………………….…….………….. 12
结束语 ………………………………………..……………….. 13
计算机输出布线图 …………………………………………… 16
参考文献 ……………………………………...... ……………. 19
(I)引言
众所周知,Moore-Lee的迷宫算法和Hightower的线探索法都是单根连线的布线算法,要解决整个电路大量线网(nets)的布线,就要把每个线网分拆成点-点间连线,然后应用这些算法对连线一根一根进行布线。这种串行布线方式速度甚慢且通常不可能获得理想结果,原因就是先布的线只能根据本身的需要确定其“最优路径”,这样就有可能布在不恰当的位置,妨碍以致完全阻塞某些后布的线,从而影响整个布线的质量和布线率。
与此相反,通道布线则是一种并行布线方法,它首先把所有线网,均匀地而不考虑其他关系,各自独立地按实际路径最短原则分配到某个或某些通道,当所有线网的通道分配完成之后,再应用通道布线算法,根据同一通道内所有线网或子线网(即被分配于2个或多个通道的部分线网)的相互关系,来确定每个线网和子线网在通道内的精确位置(在通道布线时,线网或子线网无区别,故以下不再提子线网),这种布线算法决定了它有很高的总体布线质量,且容易处理100%布线率问题[4]。
通道布线的任务是对通道内各线网进行行(track)的分配。这种算法最早由Hashmoto- Stevens[1]提出,他们的算法应用于无垂直约束的线网集可保证获得最优结果,但应用于有垂直约束的线网集结果常不理想。后来,Kernighan等人在此基础上应用分支限界法解决了这一问题[2],但运行时间较长。为此,Wada在她1981年的文章[ 4]中提出了2点改进措施,使过程有所加快,但效果不很大。本文则在所有前人工作的基础上进一步提出了许多措施,从而使算法在很多情况下可获得根本性的简化。
(I I)基本概念
1.通道模型,布线格式,最优性意义
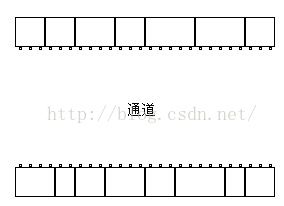
通道是一个长条形的区域,其两边为两排需要连线的电路单元。通道有连线不连续、等宽不等宽、规则不规则(若引线端的位置等间距且两边位置对齐叫规则,否则为不规则)之分,通道容量也可固定不变或浮动可变。如图1就是一个规则通道,上下有2排要相互连线的电路单元(cells),它们可能是与门、或门、非门(反相器),或有更多引线(pins)的全加器、异或门、触发器等,所有器件都有统一高度,这就是所谓的“标准单元”:
图1 一个由标准单元形成的规则通道
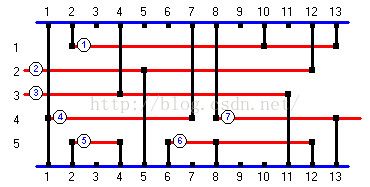
以下我们就以这种连续、等宽、规则通道为例来说明快速最优通道布线算法。一个这样的通道,我们总可以将其两边单元的引线端位置统一编号,这样,单元引线之间的连线就归结为两排整数坐标格点之间的连线。以下约定,通道为水平放置,引线端位置自左向右编号,最小为1,最大为xm(叫通道长度);上排为正,下排为负;0和xm+1表示线网向通道左边与右边的引出位置,不分正负,如下面图2a所示,其中通道长度xm=13。
|
图2a 通道内7线网的双层直干布线 2b. 线网的垂直约束图
图2a表示一内部布线已完成的通道,共布有7个线网。其中第1个线网共有3个终端(terminals),它们连着通道的3个引线位置分别是2,10,13,第2个线网连着2个引线端位置-5和12,并向通道左端引出,所以它的引线位置分别是0,-5,12,等等。每个线网都由一段水平线(干线)和几条垂直线(支线)组成。所有水平线都在同一层上,所有垂直线也在同一层上,同一线网的水平干线和垂直支线靠穿层孔(图中黑点)连接。这种布线格式叫双层直干布线。采用这种布线格式后,只要线网的水平段与水平段不重叠,垂直段与垂直段不重叠,两个线网之间一定不会重叠。本文就以这种格式为例来说明快速最优通道布线算法,但原则上,它也适用于非直杆的布线。
通道布线的“最优性”通常皆指布线占用的行数(tracks)最少。以此为目标的理由是:(1)当通道的容量固定不变时,布线需要的行数最少,达到100%布线率的可能性也最高;(2)当通道的容量可变时,布线的行数最少,意味通道需要的宽度、面积、因而也是整个VLSI芯片的面积也最小,从而在一硅片(wafer)上就可产出更多的VLSI芯片,而每个VLSI芯片的合格率也愈高。
自然,减少引线孔的数目或减少所布线网的长度也重要,为此可在获得行数最少的布线之后,再进一步优化这些参数,如[1]及其他所有作者都做的那样。
2. 线网的垂直约束,约束环,约束级别
设线网a的一个支线坐标为x,线网b的一个支线坐标为 -x,则要使线网a与b不重叠,a的干线必须布在b的干线之上,这就叫a垂直约束b,并称a是b的上辈,而b是a的下辈。显然,垂直约束关系具有传递性,设a垂直约束b,b垂直约束c,则a必垂直约束c,即a的干线必须布在c的干线之上。一个线网集的所有垂直约束关系组成一个有向图,叫垂直约束图,简称约束图,如图2b就是图2a中所有7个线网的(垂直)约束图。
设a1, a2 ,…, a k 是k个线网(k≥2),若a1垂直约束a2 , a2垂直约束a3 ,…,而a k反过来垂直约束a1,则称线网a1, a2 ,…, a k组成(垂直)约束环。如图3(A)就是由2个线网组成的(垂直)约束环。
(A) (B) (C) (D) (E)A
图3 约束环及其消去法
包含约束环的线网集不可能用直干布线方式布完所有线网。为此,可以采用曲干布线[2][4]方式来布。图3(B)就是一种曲干布线,其中水平干线有两段,并要由一垂直线段连接它们。这是第2列上下引线端都空的情况,如果第2列引线端上下都不空,则必须像图3(C)那样进行布线。
这种布线方式使带环的线网集也能100%布完所有线网,缺点则是要增加布线长度和穿层孔数目,也可能还会增加布线的行数与列数,因此应尽量不用。较好的办法是预先用程序自动检测和消除约束环,然后仍用直干布线方式进行布线。消环常用方法是修改接线或更动单元的布局方式,如图3(D)是利用上排2、3脚的逻辑等价(如都是与非门的输入)而修改接线,而3(E)则是将上边单元以2为中心作了一个x对称变换。只有万不得已的情况下才去使用曲干方式布线。
对于一无环的线网集,可以为其中每个线网定义一个约束级别(CL):没有下辈的线网的CL=1;设线网a的下辈中最大约束级别CL=k,则a的约束级别CL=k+1。如图2中,③⑥⑦的约束级别=1,②④⑤的约束级别=2,而①的约束级别最高=3。
在应用从上到下方式布线时(一般都是这样做的),约束级别高的线网应该先布,使其所在行位于通道上部,而约束级别低的但不等于1的线网应该后布,使其布在通道的下面,而约束级别等于1的线网(实际就是无任何约束的线网)则可以根据需要布在任意可布的地方,这样才能使整个布线紧凑。
3. 线网的水平重叠,重叠区(zone)
当线网a与b布在同一行时,若a布于b的左面,则b的左端点坐标必须大于a的右端点,这样a与b的干线才不致于重叠。在a右边能与a不重叠的线网一般是很多的,其中左端坐标最小者称为a右边“最左线网”,如图4中,④是①或②的最左线网,⑨是④,⑤,⑥的最左线网。
通道布线采用从上到下或从下到上布线,但在一行中,一般总以从左到右的方式进行布线。对于这种方式布线,每布下一个线网,如有可能,接着总是在其右边布其最左线网,就能最紧凑地利用各行的空间。但细心观察图4这一例子就可发现,这并不是获得紧凑布线的必要条件。我们看到,在①后布⑤、⑤后布⑦,其结果仍是最紧凑。究竟怎样最有效地利用各行空间,可以将通道划分成重叠区(zones)的结构来说明。一个zone就是通道的一个闭区间,其中所有线网或线网段都有水平重叠点;如图4中,[0,3]是一个zone,[4,10]与[11,16]也都是一个zone,一个只有三个zones。
图4 通道重叠区(zones)的划分
一个右端在zone z的线网a布下后,如有可能,接着选取左端位于z+1 zone 的任意线网进行布线,都能最紧凑地利用各行空间。因此Kernighan等人就把所有这样的线网称为a右边的最左线网。以下我们采纳这种推广的定义。
通道划分成zones后,可使通道布线过程某些环节变得紧凑[2],[4],而本文进一步利用zones的划分来为寻找优质初始布线及其他目的服务。
4. 通道密度,静态与动态界限
通道在某zone的线网密度,就是通过该zone或以该zone为起点或终点的线网总数。通道各zone的线网密度组成一个向量,叫线网密度向量,其最大元素叫通道的最大线网密度,简称通道密度[3]。如图4中3个zone的线网密度向量为为 [3,4,4],其最大元素4就是通道密度。
一个线网集S的通道密度CD(S)是S进行通道布线时需要行数的一个下界,任何布线都不可能少于这个行数,但因通道密度未考虑垂直约束关系,这个下界是不够精确的。为此,Kernighan等人在应用分支限界实现最优布线的算法[2]中,提出了所谓的“动态界限”,来估算布线需要行数。动态界限是一复杂概念,它必须与另一个叫做静态界限的概念联立递归定义产生。静态界限是对每个线网定义的,线网a的静态界限SB(a)较精确反映这个线网在一切可行布线中所能占有的起码高度。静态界限与动态界限的联立递归定义如下:
(1)无下辈的线网a的静态界限SB(a)=1;
(2)设S是一线网集,占有m个zone,其中每个线网的静态界限已定义,最大为k,则,S的动态界限,记为DB[S],按下述步骤计算:
(2a)构造一个密度矩阵D=[dij],i=1,…,k,j=1,…,m,dij就是S中静态界限为i的线网子集在zone j 的线网密度;
(2b)利用D的元素dij构造一个向量序列:
(B11 ,…,Bm1)= ( d11, …, d1m )
(B12 ,…,Bm2)= (max(2, B11+ d21), …, max(2, Bm1+ d2m) )
…….
(B1i ,…, Bmi)= (max(i, B1i-1+ di1),… ,max(i, Bmi-1+ dim) )
…….
(B1k ,…, Bmk)= (max(k, B1k-1+ dk1),…,max(k, Bmk-1+ dkm))
(2c)S的动态界限DB(S)为max(B1k,…,Bmk)
(3)设a是一线网集,DS(a)是a的下辈全体组成的集,则a的静态界限SB(a)定义为 SB(a) = DB(DS(a)) +1.
例如,在图5所示线网集S中,③与④均无下辈,故按(1)知SB(3) = SB(4) =1,②的下辈集只有1个元素④,即DS(2)={4},其动态界限按(2)的步骤可算出为1,故②的静态界限,SB(2)=DB(DS(2))+1=1+1=2;最后,①的下辈集有②,③,④三个元素,即DS(1)={2,3,4},它的动态界限DB(DS(1))按(2)的步骤可算出为3,图6(A)是计算对应的密度矩阵,故①的静态界限,SB(1)= DB(DS(1))+1=3+1=4。
(A) (B)
图5
图6 静态和动态界限的计算
对整个线网集S ={1,2,3,4},因其中每个线网的静态界限已算出,最大为4,故根据(2)可计算其动态界限db(S)如下:首先根据(2a)构造对应的密度矩阵,如图6(B)所示,再根据(2b)构造对应的向量序列,如下:
(B11 ,B21)= ( d11 , d12 ) = (1,2)
(B12 ,B22)= (max(2, B11+ d21), max(2, B21+ d22)) = (2,2)
(B13 ,B23)= (max(3, B11+ d31), max(3, B21+ d32)) = (3,3)
(B14 ,B24)= (max(4, B11+ d41), max(4, B21+ d42)) = (4,4)
最后,根据(2c)即可算出S的动态界限
DB(S)=max(4,4)=4.
可以验证,图5(A)的布线已为最优。故对此例,DB(S)就是最优布线的值VOPT(S),,也就是布线需要的最少行数,而S的最大通道密度CD(S)与最高约束级别MCL(S)都是3,小于最优布线的值VOPT(S)。
一般地,对于任意一个线网集合S,有下列结论:
VOPT(S) ≥ DB(S)…………………………….…….…………..(1)
DB(S) ≥ CD(S) ……………………………………………...(2)
DB(S) ≥ MSB(S) ≥ MCL(S) ….………………………….………..(3)
其中MSB(S)是S线网的最大静态界限。所有式中的等于和大于关系都可能成立。
我不对所有关系进行一一证明,留给读者思考,但将给出一个例子来说明(1)式中大于关系成立,即DB(S)不是衡量布线需要行数的精确值,有时会比VOPT(S)小。此例将牵涉到后面要介绍的最优算法的一个改进措施。见图7(A)::
图7(B)约束图
图7(A)通道布线
图7(C)密度矩阵和向量序列矩阵 图7(D)最优布线
这个线网集S的动态界限DB(S)=7,但最优布线(图7(D))需要8行。
如果线网集S中不含任何垂直约束,则可证明[1]:
VOPT(S) = DB(S)…………………………..…………………..(5)
DB(S) = CD(S) ……………………………………………...(6)
即(1)、(2)式中等于关系成立。
(III) 前人的通道布线算法回顾
Hashmoto-Stevens的算法[1],常称“左边算法”,是一个确定性算法。每次按一定规则选择一个线网进行布线,布完后就不再更动,直到线网布完。布线规则如下:从上到下一行一行布线,每一行内每次选择当时刚布线的线网的最左线网进行布线;如果有垂直约束,则每次选择的是无上辈或上辈已全布去的最左线网,即所谓最左合法线网[2]。
左边算法应用于无垂直约束线网集时可保证结果最优,但应用有有垂直约束的线网集时就不能保证这一点,图8就是Kernighan[2]给出的例子,该线网集的最优布线为8(B),用2行,而左边算法的布线结果为8(A),要用3行,相差1行。(注:但在本文中,由于左边算法也经过线网重排序,使第1zone中两个线网①②进行了交换,使约束级别高的②排在①前面,所以左边算法的结果也是最优,如图8(C)所示。详见后)
图8 (A) 图8 (B) 图8 (C)
一种简单的解决办法是:我们不仅从上到下从左到右布线(即左边算法),也从上到下从右到左布线(叫右边算法),从下到上左到右布线(倒左边算法),从下到上从右到左布线(倒右边算法),然后从4种结果中选其最优者。
这种简单手段有时也很有效果,例如,对于以上例子,除了左边算法布线时需要3行外,其余3种方式布线时均只需要2行,即都能获得最优解。但这是线网极少、因而可行解也很少的情况,当线网较多、因而可行解也很多时,采用这种方式就不会理想,很难得到最优解。为此,Kernighan[2]采用分支限界法以考察一切可行解。Kernighan的算法归结起来有四点:(1)采用以深为先(depth-first)方式搜索所有分支;(2)按左边算法确定分支次序;(3)分支满一行再求界,而不是分支一次求界一次;(4)由分支限界法本身产生第一个解。
Kernighan算法在分支限界过程中产生的第一个完整解,就是左边算法的解。这个解一般不是最优解,但因左边算法所用规则的逐行优化作用,这个解仍是一子优解。
利用每行布线的优化作用,可以限制其后一部分的分支。但Kernighan没有利用这一点,当某行布线完成后,通过求界发现不能导致更优解时,就要自右至左拆去所有已布线,并用新的可行布线去代替。这样,对每一行来说,一切可行布线形式都被一一考察到了,这就使工作量变得很大。
而Wada[4]考虑到这一点采取了措施,她具体提出了两点:(1)当线网a拆去后,只用左端被a覆盖的那些线网作为候选者来替代a;(2) 在求DB时,记住最后一个向量(B1k,B2k,…,Bmk)中数值达到动态界限DB的最左边的那个zone z,一旦判定须要拆除时,就可从右到左一次性地将直到zone z为止的全部线网拆去,再从这时剩下部分的布线出发继续分支和限界。
采用这两点措施后,每行的分支与求界次数就可减少,许多不能导致更优结果的布线方式就不再一一被试验了。例如按Wada的计算,对于Kernighan的第一个例子,试布的总的次数可以由原来的792次减少成207次(*) (**)。
(IV) 快速最优通道布线算法
1. 快速最优通道布线算法的基本思想
分支限界过程有2个阶段:(一)在判定树(可行解树)上依次搜索,直到获得第一个最优解;(二)验证此解的最优性,即验证此后的分支上不再有更优的解。要缩短整个过程,必须使以上两个过程都缩短。以下就是本文采取的4个措施:
(l)分层次优化:也就是首先使用一个快速优化方法作为初速布线算法以产生一个高质量的初始布线,然后(如有必要) ,再进入一般的分支限界过程去优化;
(2)采用新的最优性验证法:即除了通过分限界法本身外,还使用一种简单但常常十分有效的手段来检验已获得的解是否最优;
(3)重排线网表:即在进入分支限界过程之前,首先重新排列线网的次序, 使它有利于尽快搜索到最优解或较优解;
(4) 寻找一个能更精确估算布线需要行数的界限来代替静态界限计算中以及分支限界过程中使用的动态界限。
合理的线网排列次序, 优质的初始布线以及精确的求果方法都有利于缩短前面所说的第一个阶段, 而有效的最优性验证措施以及精确的求界方法则有利于缩短第二个阶段, 实际上,对于快速最优通道布线算法,在大都数情况下,一旦获得了最优解,整个过程也就立刻结東, 用不到象 Kernighan算法那样进行耗尽式的验证, 正是这祥它比Kenighan算法以及wada算法有高得多效率。
―――――――――――――――――――――――――――――――――――――――
(*) 本文后面也采用了这一例子,但因线网原数据排列次序不同,所得结果也不同,本文中的布线次数要小得多,如同样是用Wada算法,只要试布112行就行,见§4; (**) 在分支限界法中,试布行数应大于等于求界次数,因每试布一行至少要求界一次(最后一行例外)。
2. 初始布线算法
以下两个算法以及任何其他快速优质通道布线算法都可以作为快速最优通道布线算法的初始布线算法。
(A) 双边算法(BEA)
前面已提到, 左边算法应用于帶约束线网集通常得不到好结果,其原因在于, 它不考虑线网静态界限大小和约束级别高低,一视同仁地用左边算法規则排队, 这样那些不受任何线网约束但也不约束任何线网的“自由线网”很有可能大部分在开始阶段被布掉。而那些静态界限很大、约束级别很高的线网都因此有一部分被排挤到较低的行中,由此,到布线的后阶段,就会有许多受约束的线网因得不到足够的自由线网来填补空隙使各行布线不紧凑。
考底到这种情况,在双边算法(图9)中,每行一开始总是选择当时具有最大静态界限和最高约東级别的线网先布于“中间”, 然后在此线网右边用左边算法布线, 直到通道右端, 而在此线网左边,则用右边算法布线,直到通道左端;在同一zone中若有许多线网同时可布,则在布线之前进行的线网重排(图9框4)能首先选取静态界服大的和约東级别高的先布。
双边算法对无约束线网集可保证最优, 对有约束的线网集则一般仍然只能获得子优解, 但此子优解比左边算法的要好(見§4),另外,双边算法若不考患前面的准各工作其计算复杂性比左边算法还小, 而准各工作中大部分是分支限界法本来就需要的。
+
结束
图9 双边算法
(B)倒限界分支限界法(RBT)
这是一种限界次序与一般分支限界法完全颠倒的分支限界法。为了保证搜到任意可行解,一般分支限界法一开始必须给界限V一个很大的初始値( Kernighan定为n+l,n为线网总数),然后让V 由大到小不断用实际搜索到的布线行数来更新, 最终达到Vopt。
这一过程有可能变得很长, 这就是在判定树上可行解不是按先好后差顺序排列,而是相反,开始的解都较差,逐步出现较好的解,而最优解排在很后面。考慮到这情况, 倒限界分支限界法一开始就用整个线网集S的动态界限DB(S)作为V的初值,以加快剪支速度,如果发现不存在实际的解能达到V时, 再放宽V,即V=V+1再试。这样由小到大来逼近Vopt。
倒限界分支限界法可以是完全优化的, 也可以是部分优化的。 作为初始布线算法, 以下介绍一个部份优化的倒限界分支限界法, 这是一个逐行应用分支限界法而整个不用的快速算法,图10是采用分zone结构的倒限界算法,具体步骤说明如下:
① 计算整个集合S的动态界限DB(S),令v=DB(S),行数t=1,已布线网数s=0;
② 用左边算法在t行布线,当布满一行时,计算未布线网集的动态界限DB,判别关系式t+DB<=V是否成立?若成立就t+1去布下一行,否则就按后布先拆的顺序,将t行上位于右边的线网拆除(擦除规则同Wada,见框图),并用某些最左线网继续布满t行(选择规则同Wada,见框图);再计算未布线网集的DB并判别关系式t+DB<=V是否成立?…,这样不断用尚有可能满足关系式的各种可行布线来试布该行。最后有两种可能:在某种布线下t+DB<=V成立,这时就t+1 去布下一行,否则,即
③ 在一切可行布线下都不能使关系式t+DB<=V成立,这时就取本行各种可行布线中性能最好的一种、即能使未布线网集的动态界限达到最小值minDB的那种布线作为本行布线,并令V=t+minDB,然后再t+1,转②,去布下一行;这样一直下去直到s=n即线网布完。
框图如下(图l0)
图l0 倒限界分支限界法
上图中s为已布线网集;z为当前布线起始zone;ZL、ZR为实现Wada加速技巧引进的两个参数;R是一个标志,取1时代表当前为布线,取0为拆线;n是线网总数。
作为例子,考察图11(A)所示线网集, (B)为其约束图, (C)(D)(E)分别为Kernighan、Wada与倒限界三个算法过程的比较,这里我们用判定树上经历的路径来描述執行过程,正反向箭头表示布线和拆线,圆圈代表求界,圆内数字为t+DB的值。(F)为三算法共同结果,一共都使用3行完成全部线网的布线。
图11 倒限界法与Kernighan算法、Wada算法分支过程比较
由图可見,倒限界算法能最快得到最优解,算法执行时拆线只有1次。一般地,只要每次所求界限都是精确值,则此算法可保证结果最优。这个结论表明, 倒限界分支限界法是一个由已知精确求界方法来迅速寻找最优解的系统性方法。
作为特例,对于无约束线网集,因动态界限DB是最优布线的精确界限(见§II公式(4),(5)),故可保证最优解。
另外,上述结论只是一个充分条件,就是说,所求界限不是每次精确时,也常有可能获得最优解,如对于图5所示线网集,倒限界分支限界法同样可得最优解。
4.最优性验证
当最优解得到之后,要验证此解的最优性,即证明在判定樹上其后的一切分支上没有比此更优的解, Kernighan(或Wada)采用的方法是继续进行耗尽式的搜索.直到没有发现更优解,这种方法对于“大边缘问题”,即可行解数量很大的布线间题,就要化费很多时间。 Kernighan举了一个例子,它的最优解一秒钟内就找到了,但验证最优性却化费了20分钟(*)。为了解决这一困难, Kernighan提出用控制运行时间的办法,即程序运行了足够长的时间后就中断运行。显然,这种方法是不可靠的,因为当判定树上最优解排在很后面时就需要化费很长时问才能搜索到第一个最优解(見计算结果FO1一栏)。
(*)这个例子的具体数据情况在[2]中未给出,本文另外给了一个类似的例子。
在快速最优通道布线算法中采用的办法是:在分支展界开始前,先计算整个线网集S的动态界限DB(S),然后,每当得到一个新解时.就检査它的值是否=DB(S),如果相等,则根据§公式(3),就可断定此解为最优,整个过程就可结東, 就用不到进行耗尽式的验证,如果不等,则才让它继续分支限界下去。
这一措施是否有效也决定于所求界限的精确性(对 Kernighan 所举的例子来说本措施全有效)。但与倒限界法保证最优解所需条件不同,这里只要对整个集合的一次求界为精确値就可以了,这就容易得到, 实际遇到的问题绝大部分能做到这一点。
5. 重排线网的次序
这一措施的目的是让最优解或较优解尽可能地排在判定樹上较早授索到的那些分支上。判定树的结构由分支规则(左边算法)确定,但因最左线网一般不是唯一的,因而如何分支,即先选什么线网后选什么线网, 有了灵活性。 这就使判定树的结构在一定程度上可以改变。本措具体的做法是:在约束级别和静态界限求出之后,將各zone中的起始线网重新排队,使静态界限大的排在前面, 如果静态界限一致,则使约東级别高的排在前面;而在进入分支限界后每次都按线网的这种先后顺序来选择下一最左线网。 (*)
6.寻找一种新的界限
精确的求界方法对分支限界法的快速剪枝有帮助, 对上面提出的倒限界分支限界法以及最优性验证法来说则更重要。 Kernighan的动态界限在一般例子中是相当精确的, 但在特殊情况下有可能变差。分析其原因,在于:它考虑了线网的水平重量关系,也考虑了它们的垂直约束关系, 但没有考虑在布线过程中由相互重叠的线网引起的新的垂直约束关系。例如在图7中,线网①.与⑤.⑨並无约束关系,只要它们水平不重量,就可以共行(如①与⑨), 但是, 因①②水平重叠,必须放在不同行上,这样,如果①放在②上,则①也就必须在⑤⑨之上, (从而使①不能与⑨共行),这就是新的约束关系。
这种新约束关系使动态界限在估算布线需要行数时有时要失敗(变小)。上例就是如此。因为,①与⑨之同无约東关系且不重盘, ②与⑥之同也是这样。但在实际布线之中,这两对线网之间必有一对产生了新的约束关系,而DB的计算中没有考慮到这种情况。
由这一例子的启发,我们可以引进一种估算布线需要行数的更精确的方法(见图12 ) : 从原来的线网集S形成两个新的线网集Sl与S2,在Sl中①约束②, S2中②约束①;然后,分别计算Sl与S2的动态界限:DB(S1), DB(S2);而S的新动态界限:
NDB(S)= min(DB( S1), DB(S2))。
图12 新的动态界限及计算
按此方法计算, S的新动念界限等于8,也即布线实际需要行数的精确下界。 但是,在一般情状下,要完整考察线网重叠引起的垂直约束是非常复杂的。必须简化才行,简化的原则就是只考察最有可能引起新约束关系的少数线网, 这就是静态界限很大约束级别最高的那些线网。
7. 快速最优通道布线算法
将上述加快措施中的一个、两个或相容的多个加到Kernigha:n算法或Wada算法中去,就可得到一系列的改进算法,例如以下形式都是可取的:
A:在Kernighan算法加进Wada的两个加快措施后得到的改进形式基础上, 再增加新的最优性验证措施。这是一个容易修改、容易得到效果而增加的工作只是一次动态界限的计算。
B:在A基础上,采用倒限界分支限界法作为初始布线算法。这一修改将使包含5 0个线网的布线问题在小型机上可能增加l移钟的计算时同,但由此可使分支限界过程缩短的时同有时可100倍于此。程序並不要重编,只要在原来算法基础上插入少数判别语句和执行语句就可以实现这个初始布线。
C:在B基础上采用线网重排措施。重排线网,通常可改善左边算法或倒限界法的结果, 有时单独使用它就可使左边算法获得最优解。在 B基础上再加上这一措施一般也是有益的,但对B本身已能获得最优结果的问题就要增加一点点运行时间如0.l秒。
D:在C基础上,再加上新的动态界限计算方法。这一措施对“困难”间题来说会是很有益的, 但对于“容易的”问题则反而会因为措施本身的工作量而使计算复杂化。因此必须选择使用, 选择的方法是:先计算被布集合S的动态界限DB(S),再用倒限界分支限法进行布线,若布线需要行数V与DB(S)之差≤ l ,则说明最多只要用分支限法来改善l个 track, 就不用新措施, 否则,如果大于l,就可采用它。
E:在A基础上,采用双边算法作为初始布线算法,这一形式大体和C一致。
F:在E基础上加上新动态界限计算方法。这一步应和D一样,是应有选择的,选择方法类似D。
(V) 运行结果比较
以下表1是在PDP11/34小型机上对几个算法的部分运行结果, 7个例子中除最后一个外,其余全部来源于[2] ,而第7个是人为构造出来的例子,它包含50个线网,无垂直约束,有大量的可行解,这一例子用来说明采用耗尽式最优性验证的致命缺点。
算法共列出8个,如下:
ΔLEA -- 左边算法,采用了分zone措施;
ΔBEA -- 双边算法;
ΔRBT -- 倒限界部分优化分支限界法,预先重排了线网;
ΔFOA -- Wada算法中加进新的最优性验证技术;
ΔFOB -- 采用倒限界分支法作为初始布线算法的 FOA;
ΔFOC -- 预先重排序的FOB;
ΔFOD -- 倒限界完全优化的分支限界法。
ΔWada -- 即在 Kernighan的最优通道布线算法基础上,采用了Wada的两个加速措施后的改进形式;
程序是在分时操作系统中运行的, 因而统计时间仅可作参考, 算法的效率可从其分支和求界次数的多少获得精确比较,后者即使机器速度改变也不会变。
以双边算法为初始布线算法的快速最优布线我们没有列出来, 但其结果大体可从双边算法本身的效率看出。
从表l可以看出, 双边算法BEA、倒限界法RBT1是两个很好的启发式算法, 它们对所有例子运行结果与最优解行数相差都不大于1 , 且大部分获得了最优解. 特别是RBTl。这两个算法完全可以独立地使用。
(VI) 结束语
已经证明,通道布线问题是NP完备的,因此,随著大規模集成电路规模的不断扩大, 采用分支限界法必然会遇到十分困难的间题。但是要看到,计算机的遠度也在飞快提高,並且,我们不一定要对整个大規模集成电路采用一次布线的方法, 而可以利用分层次通道布线。这一思想已经被许多事实如〔5〕证明是可行的,在此文章中報导了用分层次多元胞布线方法设计了一个32位 CMOS超大規模集成电路微处理器。
(*)如果以双边算法为初始布线算法, 则此步骤已预先完成.
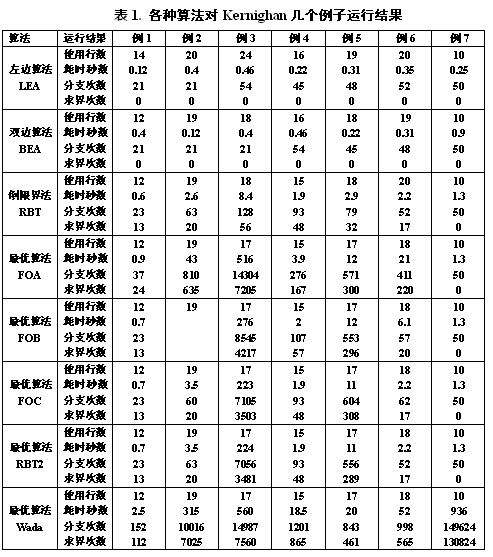
表1. 各种算法对Kernighan几个例子运行结果
| 算 法 |
运行结果 |
例1 |
例2 |
例3 |
例4 |
例5 |
例6 |
例7 |
|
左边算法LEA
|
使用行数 耗时秒数 分支次数 求界次数 |
14 0.12 21 0 |
20 0.4 21 0 |
24 0.46 54 0 |
16 0.22 45 0 |
19 0.31 48 0 |
20 0.35 52 0 |
10 0.25 50 0 |
|
双边算法BEA |
使用行数 耗时秒数 分支次数 求界次数 |
12 0.4 21 0 |
19 0.12 21 0 |
18 0.4 21 0 |
16 0.46 54 0 |
18 0.22 45 0 |
19 0.31 48 0 |
10 0.9 50 0 |
|
倒限界法 RBT |
使用行数 耗时秒数 分支次数 求界次数 |
12 0.6 23 13 |
19 2.6 63 20 |
17 8.4 128 56 |
15 1.9 93 48 |
18 2.9 79 32 |
20 2.2 52 17 |
10 1.3 50 0 |
|
最优算法 FOA |
使用行数 耗时秒数 分支次数 求界次数 |
12 0.9 37 24 |
19 43 810 635 |
17 516 14304 7205 |
15 3.9 276 167 |
17 12 571 300 |
18 21 411 220 |
10 1.3 50 0 |
|
最优算法 FOB |
使用行数 耗时秒数 分支次数 求界次数 |
12 0.7 23 13 |
19
|
17 276 8545 4217 |
15 2 107 57 |
17 12 553 296 |
18 6.1 57 20 |
10 1.3 50 0 |
|
最优算法FOC |
使用行数 耗时秒数 分支次数 求界次数 |
12 0.7 23 13 |
19 3.5 60 20 |
17 223 7105 3503 |
15 1.9 93 48 |
17 11 604 308 |
18 2.2 62 17 |
10 1.3 50 0 |
|
最优算法FOD |
使用行数 耗时秒数 分支次数 求界次数 |
12 0.7 23 13 |
19 3.5 63 20 |
17 224 7056 3481 |
15 1.9 93 48 |
17 11 556 289 |
18 2.2 52 17 |
10 1.3 50 0 |
|
最优算法 Wada |
使用行数 耗时秒数 分支次数 求界次数 |
12 2.5 152 112 |
19 315 10016 7025 |
17 560 14987 7560 |
15 18.5 1201 865 |
17 20 843 461 |
18 52 998 565 |
10 936 149624 130824 |
I 参考文献
[1] Hashimoto-Stevens: Wire routing by optimizing channel assigment with large aperture, proc. 8th DAC,1971
[2] B.W.Kernighan, D.G.Schweikert, G.Persky: An optimun channel routing algorithm for polycell layouts of integrated circuit, proc 10th DAC 1973;
[3] D.A.Deutch: A “Dogleg” channel router, proc. 13th DAC 1976;
[4] M.M. Wada: An “optimal” dogleg channel router with completion enhancement, proc. 18th DAC,1981;
[5] S. Horiguchi, H. Yoshimura, et. el: An Automatically designed 32b CMOS VLSI Processor, Degest of technical papers, 1982 IEEE International Solidstate Circuit conference.
[6] 吴祖增:快速最优通道布线算法,半导体学报,1993年4月
[7] blog.csdn.net/zzwu/article/details/825386
下面将详细介绍各种算法(插图待加)
说明:本文系1982年我为昆明召开的全国CAD会议提供的两篇稿件之一。当时供给会议的份数很少,且系打字油印,图形以手工刻画,质量极差,还有不少错漏,为此深感遗憾,一直以来希望有朝一日能改正后重新发表。1983年我做了这个工作,并向《半导体》学报投过稿,但因字数大大超过5000而未能发表,后来从中删去大量重要内容才得发表。但我估计此文很少有人能看懂此文,包括中外行内专家,故用单行本正形式全文发表。但长期来因原手稿和油印稿均找不到无法完成此工作。最近找到一份油印稿,我花了很多精力将其错误改正,缺少的补上,并将所有插图改用计算机软件清晰输出,决定在此正式发表。注:另一篇《崎岖通道最优布线》采取同样措施后早在CSDN博客上发表了,见
http://blog.csdn.net/zzwu/article/category/2856801
【摘要】 本文提出的几个快速最优通道布线算法(FOCR)是Kernighan-Schweikert-Persky最通道布线算法[2]和Wada最优曲干通道布线算法[ 4]的改进,这些算法的“最优性”意义完全相同,但新算法执行速度比原有算法远远为快,一般情况下统计地可相差几倍到十几倍,极端情况下则可相差更多数量级。
【关键字】双层直干通道布线,垂直约束与约束环,水平重叠与重叠区,通道密度,静态与动态界限,Kernighan和Wada的最优通道布线算法,Deutche困难问题。
(一)引言
众所周知,Moore-Lee的迷宫算法和Hightower的线探索法都是单根连线的布线算法,要解决整个电路大量线网(net)的布线,就要把每个线网分解成点到点的连线,然后利用这类算法来一根根地布这些点-点间连线。这种串行布线方式不仅速度慢且通常不可能获得理想结果,原因就是先布的线只能根据本身的需要确定其“最优路径”,这样就有可能布在不恰当的位置,妨碍以致完全阻塞某些后布的线,从而影响整个布线的质量和布线率。
与此相反,通道布线则是一种并行布线方法,它首先把所有线网,均匀地、不考虑相互影响、各自独立地按实际路径最短原则分配到某个或某些通道,当所有线网的通道分配完成之后,再应用通道布线算法,根据同一通道内所有线网或“子线网”(即线网一部分,或部分线网。有时一个大线网要拆分成位于多个通道的部分线网。在通道内布线时,线网或子线网无区别,故以下不再提子线网概念)的相互关系,来确定每个线网在通道内的精确位置,这种布线算法决定了它有很高的总体布线质量,且容易处理100%布线率问题[4]。
通道布线算法的任务是对通道内各线网进行track(行)的分配。这种算法最早由Hashmoto-Stevens[1]提出,他们的算法应用于无垂直约束的线网集可保证获得最优结果,但应用于有垂直约束的线网集结果常不理想。后来,Kernighan等人在此基础上应用分支限界法解决了这一问题[2],但运行时间较长。为此,Wada在她1981年的文章[4]中提出了2点改进措施,使过程有所加快,但效果不很大。本文则在所有前人工作的基础上进一步提出了一系列措施,从而使算法在很多情况下可获得根本性的简化。
(二)基本概念
1.通道模型,布线格式,最优性意义
通道是一个长条形的区域,其两边为两排需要连线的电路单元。通道有连线不连续、等宽不等宽、规则不规则(若引线端的位置等间距且两边位置对齐叫规则,否则为不规则)等多种形式,以下以连续、等宽、规则通道为例来说明快速最优通道布线算法。
图1 一个通道
一个这样的通道,我们总可以将其两边单元电路的引线端位置统一编号,这样,单元与单元之间的连线就归结为两排整数坐标格点之间的连线, 如图2a所示。以下约定,通道为水平放置,引线端位置自左向右编号,最小为1,最大为xm;上排为正,下排为负;0和xm+1表示线网向通道左边与右边的引出位置,不分正负。
|
|
|
图2a 通道内双层直干布线 2b 垂直约束图
图2a表示内部布线已完成的通道,其中共有7个线网,每个线网都由一段水平线(干线),和几条垂直线(支线)组成。所有水平线(红色)都在同一层上,所有垂直线(黑色)也在同一层上,同一线网的水平干线和垂直支线靠穿层孔(图中黑点)连接。
这种布线格式叫双层直干布线。采用这种布线格式后,只要线网的水平段与水平段不重叠,垂直段与垂直段不重叠,两个线网之间一定不重叠。本文就以这种格式为例来说明快速最优通道布线算法,但原则上,它也适用于非直杆的布线,见后。
通道布线的“最优性”通常皆指布线占用的行数(tracks)最少。以此为目标的理由是:(1)当通道的容量固定不变时,布线需要的行数最少,达到100%布线率的可能性也最高;(2)当通道的容量可变时,布线的行数最少,意味通道需要的宽度、面积、因而也是整个VLSI芯片的面积也最小,从而在一硅片(wafer)上就可产出更多的VLSI芯片,而每个VLSI芯片的合格率也愈高。
自然,减少引线孔的数目或减少所布线网的长度也重要,为此可在获得行数最少的布线之后,再进一步优化这些参数,如[1]及其他所有作者都做的那样。
2. 线网的垂直约束,约束环,约束级别
设线网a的一个支线坐标为x,线网b的一个支线坐标为 -x,则要使线网a与b不重叠,a的干线必须布在b的干线之上,这就叫a垂直约束b,并称a是b的上辈,而b是a的下辈。显然,垂直约束关系具有传递性,设a垂直约束b,b垂直约束c,则a必垂直约束c,即a的干线必须布在c的干线之上。一个线网集的所有垂直约束关系组成一个有向图,叫垂直约束图,简称约束图,如图2b就是图2a中所有线网组成的线网集的(垂直)约束图。
设a1,a2 ,…,a k 是k个线网,k≥2,若a1垂直约束a2 , a2垂直约束a3 ,…,而a k反过来又垂直约束a1,则称线网a1,a2 ,…,a k组成(垂直)约束环。如图3(A)就是由2个线网组成的(垂直)约束环。
图3 约束环及其消去法
包含约束环的线网集不可能用直干布线方式布完所有线网。为此,可以采用曲干布线[2][4]方式来布。图3(B)就是一种曲干布线,其中水平干线有两段,并要由一垂直线段连接它们。这是第2列上下引线端都空的情况,如果第2列引线端上下都不空,如必须像图3(C)那样进行布线,这种布线方式使带环的线网集也能100%布完所有线网,缺点则是要增加布线长度和穿层孔数目,也增加了布线的行数与列数,因此应尽量不用。较好的办法是预先用程序自动检测和消除约束环,然后仍用直干布线方式进行布线。消环常用方法是修改接线或更动单元的布局方式,如图3(D)是利用上排2、3脚的逻辑等价(如都是与非门的输入)而修改接线,而3(E)则是将下边单元作了一个Y轴的对称变换。只有万不得已的情况下才去使用曲干方式布线。
对于一无环的线网集,可以为其中每个线网定义一个约束级别(CL):没有下辈的线网的CL=1;设线网a的下辈中最大约束级别CL=k,则a的约束级别CL=k+1。如图2中,③⑥⑦的约束级别=1,②④⑤的约束级别=2,而①的约束级别最高=3。
在应用从上到下方式布线时(一般都是这样做的),约束级别高的线网应该先布,使其所在行位于通道上部,而约束级别低的但不等于1的线网应该后布,使其布在通道的下面,而约束级别等于1的线网(实际就是无任何约束的线网)则可以根据需要任意布在可能布的地方,这样才能使整个布线紧凑。
3. 线网的水平重叠,重叠区(zone)
当线网a与b布在同一行时,若a布于b的左面,则b的左端点坐标必须大于a的右端点,这样a与b的干线才不致于重叠。在a右边能与a不重叠的线网一般是很多的,其中左端坐标最小者称为a右边“最左线网”,如图4中,④是①或②的最左线网,⑨是④,⑤,⑥的最左线网。
通道布线可以采用从上到下或从下到上布线,但在一行中,总是从左到右的方式进行布线。对于这种方式布线,每布下一个线网,如有可能,接着总是在其右边布其最左线网,就能最紧凑地利用各行的空间。但细心观察图4这一例子就可发现,这并不是获得紧凑布线的必要条件。我们看到,在①后布⑤、⑤后布⑦,其结果仍是最紧凑。究竟怎样最有效地利用各行空间,可以将通道划分成重叠区(zones)的结构来说明。一个zone就是通道的一个闭区间I,满足以下2个条件:
(1)I中所有线网两两水平重叠;
(2)设区间I’是区间I的扩充,则I’中就有不重叠的线网。
如图4中,[0,3]是一个zone,[4,10]与[11,16]也都是一个zone,一个只有三个zones。
图4 通道重叠区(zones)的划分
一个右端在zone z的线网a布下后,如有可能,接着选取左端位于z+1 zone 的任意线网进行布线,都能最紧凑地利用各行空间。因此Kernighan等人就把所有这样的线网称为a右边的最左线网。以下我们采纳这种推广的定义。
通道划分成zones后,可使通道布线过程某些环节变得紧凑[2],[4],而本文进一步利用zones的划分来为寻找优质初始布线及其他目的服务。
4. 通道密度,静态与动态界限
通道在某zone的线网密度,就是通过该zone或以该zone为起点或终点的线网总数。通道各zone的线网密度组成一个向量,叫线网密度向量,其最大元素叫通道的最大线网密度,简称通道密度[3]。如图4中3个zone的线网密度向量为为 [3,4,4],其最大元素4就是通道密度。
一个线网集S的通道密度CD(S)是S进行通道布线时需要行数的一个下界,任何布线都不可能少于这个行数,但因通道密度没有考虑垂直约束关系,这个下界是不够精确的。为此,Kernighan等人在应用分支限界实现最优布线的算法[2]中,提出了所谓的“动态界限”,来估算布线需要行数。动态界限是一复杂概念,它必须与另一个叫做静态界限的概念联立递归定义产生。静态界限是对每个线网定义的,线网a的静态界限SB(A)较精确反映这个线网在一切可行布线中所能占有的起码高度。静态界限与动态界限的联立递归定义如下:
(1)无下辈的线网a的静态界限SB(a)=1;
(2)设S是一线网集,占有m个zone,其中每个线网的静态界限已定义,最大为k,则,S的动态界限,记为DB[S],按下述步骤计算:
(2a)构造一个密度矩阵D=[dij],i=1,…,k,j=1,…,m,dij就是S中静态界限为i的线网子集在zone j 的线网密度;
(2b)利用D的元素dij构造一个向量序列:
(B11 ,…,Bm1)= ( d11, …, d1m )
(B12,…,Bm2)=(max(2, B11+ d21), …, max(2, Bm1+d2m) )
…….
(B1i,…, Bmi)=(max(i, B1i-1+ di1), …, max(i, Bmi-1+dim) )
…….
(B1k ,…, Bmk)= (max(k, B1k-1+ dk1),…,max(k,Bmk-1+ dkm))
(2c)S的动态界限DB(S)为max(B1k,…,Bmk)
(3)设a是一线网集,而DS(a)是a的下辈全体组成的集合,则a的静态界限,SB(a),定义为
SB(a) = DB(DS(a)) +1.
例如,在图5所示线网集S中,③与④均无下辈,故按(1)知SB(3)= SB(4) =1,②的下辈集只有1个元素④,即DS(2)={4},其动态界限按(2)的步骤可算出为1,故②的静态界限,SB(2)=DB(DS(2))+1=1+1=2;最后,①的下辈集有②,③,④三个元素,即DS(1)={2,3,4},它的动态界限DB(DS(1))按(2)的步骤可算出为3,图6(A)是计算对应的密度矩阵,故①的静态界限,SB(1)= DB(DS(1))+1=3+1=4。、
(A) (B)
图5
(A) (B)
图6
对整个线网集S ={1,2,3,4},因其中每个线网的静态界限已算出,最大为4,故根据(2)可计算其动态界限db(S)如下:首先根据(2a)构造对应的密度矩阵,如图6(B)所示,再根据(2b)构造对应的向量序列,如下:
(B11 ,B21)= ( d11 , d12 ) = (1,2)
(B12 ,B22)= (max(2, B11+ d21),max(2, B21+ d22)) = (2,2)
(B13 ,B23)= (max(3, B11+ d31),max(3, B21+ d32)) = (3,3)
(B14 ,B24)= (max(4, B11+ d41),max(4, B21+ d42)) = (4,4)
最后,根据(2c)即可算出S的动态界限
DB(S)=max(4,4)=4.
可以验证,图5(A)的布线已为最优。故对此例,DB(S)就是最优布线的值VOPT(S),,也就是布线需要的最少行数,而S的最大通道密度CD(S)与最高约束级别MCL(S)都是3,小于最优布线的值VOPT(S)。
一般地说,对于任意一个线网集合S,有下列结论:
VOPT(S) ≥ DB(S)…………….…….…………..(1)
DB(S) ≥ CD(S) ……………………………...(2)
DB(S) ≥ MSB(S) ≥ MCL(S) ….…………..(3)
其中MSB(S)是S线网的最大静态界限。所有式中的等于和大于关系都可能成立。
我不对所有关系进行一一证明,这留给读者思考,但将给出一个例子来说明(1)式中大于关系成立,即DB(S)也不是衡量布线需要行数的精确值,有时会比VOPT(S)小。此例将牵涉到后面要介绍的最优算法的一个改进措施。见图7(A)::
FOCR插图
密度矩阵 向量序列矩阵
这个线网集S的动态界限DB(S)=7,但最优布线(图7(B))需要8行。
如果线网集S中不含任何垂直约束,则可证明[1]:
VOPT(S) = DB(S)…………….…….…………..(5)
DB(S) = CD(S) ……………………………...(6)
即(1)、(2)式中等于关系成立。
(四)快速最优通道布线算法
1. 关于前人的通道布线算法
Hashmoto-Stevens算法[1],常称“左边算法”,是一个确定性算法。每次按一定规则选择一个线网进行布线,布完后就不再更动,直到线网布完。布线规则如下:从上到下一行一行布线,每一行内每次选择当时刚布线的线网的最左线网进行布线;如果有垂直约束,则每次选择的是无上辈或上辈已全布去的最左线网,即所谓最左合法线网[2]。
左边算法应用于无垂直约束线网集时可保证结果最优,但应用有有垂直约束的线网集时就不能保证这一点,图8就是Kernighan[2]给出的例子,该线网集的最优布线为8(B),用2行,而左边算法的布线结果为8(A),要用3行,相差1行。
图8
一种简单的解决办法是:我们不仅从上到下从左到右布线(即左边算法),也从上到下从右到左布线(叫右边算法),从下到上左到右布线(倒左边算法),从下到上从右到左布线(倒右边算法),然后从4种结果中选其最优者。
这种简单手段有时也很有效果,例如,对于以上例子,除了左边算法布线时需要3行外,其余3种方式布线时均只需要2行,即都能获得最优解。但这是线网极少、因而可行解也很少的情况,当线网较多、因而可行解也很多时,采用这种方式就不够理想,很难得到最优解。为此,Kernighan[2]采用分支限界法以考察一切可行解。Kernighan的算法归结起来有四点:(1)采用以深为先法(depth-first)搜索所有分支;(2)按左边算法确定分支次序;(3)分支满一行再求界,而不是分支一次求界一次;(4)由分支限界法本身产生第一个解。
Kernighan算法在分支限界过程中产生的第一个完整解,就是左边算法的解。这个解一般不是最优解,但因左边算法所用规则的逐行优化作用,这个解仍是一子优解。
利用每行布线的优化作用,可以限制其后一部分的分支。但Kernighan没有利用这一点,当某行布线完成后,通过求界发现不能导致更优解时,就要自右至左拆去所有已布线,并用新的可行布线去代替。这样,对每一行来说,一切可行布线形式都被一一考察到了,这就使工作量变得很大。
而Wada[4]考虑到这一点采取了措施,她具体提出了两点:(1)当线网a拆去后,只用左端被a覆盖的那些线网作为候选者来替代a;(2) 在求DB时,记住最后一个向量(B1k,B2k,…,Bmk)中数值达到动态界限DB的最左边的那个zone Z,一旦判定须要拆除时,就可从右 到左一次性地将直到zone Z为止的全部线网拆去,再从这时剩下部分的布线出发继续分支和限界。
采用这两点措施后,每行的分支与求界次数就可减少,许多不能导致更优结果的布线方式就不再一一被试验了。例如按Wada的计算,对于Kernighan的第一个例子,试布的总的次数可以由原来的792次减少成207次(*) (**)。
―――――――――――――――――――――――――――――――――――――――
(*) 本文后面也采用了这一例子,但因线网原数据排列次序不同,所得结果也不同,本文中的布线次数要小得多,如同样是用Wada算法,只要试布112行就行,见§4; (**) 在分支限界法中,试布行数应大于等于求界次数,因每试布一行至少要求界一次(最后一行例外)。
2. 快速最优通道布线算法的基本思想
分支限界过程有2个阶段:(一)在判定树(可行解树)上依次搜索,直到获得第一个最优解;(二)验证此解的最优性,即验证此后的分支上不再有更优的解。要缩短整个过程,必须使以上两个过程都缩短。以下就是本文采取的4个措施:
(1)分层次优化:也就是先用一个快速布线算法作为初始布线,然后(如有必要)再入一般的分支限界过程去优化;
(2)采用新的最优性验证法:即除了通过分銀果法本身外,还使用一种简单但常常十分有效的手段来检验已获得的解是否最优;
(3)重排线网表:即在进入分支限界过程之前,首先重新排列线网的次序, 使它有利于尽快搜索到最优或较优解;
(4) 寻找一个能更精确估算布线需要行数的界限,来替代静态界限计算中以及分支限界过程中使用的动态界限。
合理的线网排列次序, 优质的初始布线以及精确的求果方法都有利于前面所说的第一个阶段, 而有效的最优性验证措施以及精确的求界方法则有利于第二个阶段的缩短, 实际上,对于快速最优通道布线算法,在大都数情况下,一旦获得'了最优解,整个过程也就立刻结束, 用不到象Kernighan或Wada算法那本进行耗尽式的验证,正是这祥它比Kernighan算法以及Wada算法有高得多的效率。
3. 初始布线算法
以下两个算法以及任何其他快速优质通道布线算法都可以作为快速最优通道布线算法的初始布线算法。
----------
(*) 本文也采用了这一例子,但因线网原始数据排列次序不同,所得结果也不同,本文中的数字要小得多,如用 Wada算法, 只要试布1l2行次,见e野。
(**) 试布行数应大体等于求界次数,国每布一行都要求界一次(最后一行可例外)。
(A) 双边算法( BEA)
前面已经提到, 左边算法应用于帶约束线网集通常得不到好的结果,原因在于,它不考虑线网静态界限大小和约束级别高低都一视同仁地用左边算法規则来排队,这样那些不受任何线网约束但也不约束任何别的线网的“自由线网”很有可能大部分在开始阶段被布掉,而那些静态界限很大约束级别很高的线网都因此有一部分被排挤到较低的行中,由此,到布线的后阶段,就会有许多受约束的线网因得不到足够的自由线网来填补空隙使各行布线不紧凑。
考底到这种情况,在双边算法(国9)中,每行一开始总是选择当时具有最大静态界限和最高约束级别的线网先布于“中同”, 然后在此线网右边应用左边算法布线,直到通道右端。而在此线网左边,则应用右边算法布线,直到通道左端;另外,在同一zone 中若有许多线网同时出发,则在布线之前进行的线网重排(图9框4) 能保证首先选取静态界服大的和约束级别高的。
双边算法对无约束线网集可保证最优,对约束集则一般伤然只能获得子优解。 但此子优解比左边算法的子优解要好得多(見S:lS计算结果),另外,双边算法著不考患前面的准各工作其计算复杂性比左边算法还小,而准各工作中大部分是分支限界法本来就需要的。
(B)倒限界分支限界法(RBT)
这是一种限界次序与一般分支限界法颠倒的分支限界法 。 为了保证获得解,在一般的分支限界法中,一开始必须给界限V一个很大的初始値( Kornighan算法为 n+l ,n为线网总数),然后让 V由大到小不断用实际搜索到的解的值来更新,最终达到最优值Vopt。
这一过程有可能变得很长,这就是在判定树上可行解不是按先好后差的顺序排列,而是相反。开始的解都较差,逐步地出现较好的解,而最优解排在很后面。
考慮到这一情况,倒限界分支限界法一开始就用一个下界作为V的初值,以加快剪支速度,如果发现不存在实际的解能达到 V时,再放宽V,即 V:= V+1,再试验。这样由小到大地来逼近最优值。
倒限界分支限界法可以是完全优化的,也可以是部分优化的。 作为初始布线算法,以下介绍一个部份优化的倒限界分支限界法,这是一个逐行应用分支限界法而整个不用的快速算法,具体步骤如下:
①计算整个线网集合S的动态界限DB(S) ,令V=DB(S),行数t=1, 已布线网数s=0;
②用左边算法在t行布线,每布一线网,s+1,並将被布线网号送布线单作为第 s号元素,直到 t行满(无线网可布于t行)为止;
③检査s是否已等于线网总数n,若等于,布线结束;
④ 计算这时的未布线网集的动态界限DB,判别 t+DB是否≤ V,若成立,转⑤;若t+DB>V,则接Wada方法拆去布线单中属于该行的一部分布线,再转②去布新线网;若t+DB>V,而布线表中属于该行的布线已全拆完,且在②中又无新的线网可布时,则转⑥ ;
⑤ t行布线已完成,故t+1,转②去布下一行;
⑥令V=V+1(或V= t+最小DB),转②,去重布t 行。
框图如下(图10)
图l0 倒限界分支限界法
作为例子,考察图8所示线网集。算法的新进程如图11(A) 所示,这里我们用判定树上经历的路径来描述算法的執行过程,正反向箭头表示布线和拆线,圆圈代表求界,圆内数字为t+DB的值。
图形左边数字为所得可行解值,整个过程包含布线(分支)4次,拆线1次,求界3 次。图11(B)、(C)为 Kernighan最优通道布线算法(OCR)和Wada算法的执行过程,(D)为完整的判定樹,即穷举法的执行过程(但这时求界过程全可以省去) 。
由图可見,倒限界算法能最快得到最优解。一般地,只要每次所求界限都是精确值,则此算法可保证结果最优。这个结论表明,倒限界分支限界法是一个由已知精确求界方法来迅速寻找最优解的系统性方法。
作为特例,对于无约束线网集,因动态界限DB是最优布线的精确界限(见§II公式(4),(5)),故可保证最优解。
另外,上述结论只是一个充分条件,就是说,所求界限不是每次精确时,也常有可能获得最优解,如对于图5所示线网集,倒限界分支限界法同样可得最优解。
4.最优性验证
当最优解得到之后,要验证此解的最优性,即证明在判定樹上其后的一切分支上没有比此更优的解,Kernighan或Wada采用的方法是继续进行耗尽式的搜索,直到没有发现更优解。这种方法对于“大边缘问题”,即可行解数量很大的布线间题,就要化费很多时间。 Kernighan举了一个例子,它的最优解一秒钟内就找到了,但验证最优性却化费了20分钟(*)。为了解决这一困难,Kernighan提出用控制运行时同的办法,即程序运行了足够长的时间后就中断运行。显然,这种方法是不可靠的,因为当判定树上最优解排在很后面时就需要化费很长时问才能搜索到第一个最优解(見计算结果FO1一栏)。
(*)这个例子的具体数据在[2]中未给出,本文另外给了一个类似的例子。
在快速最优通道布线算法中采用的办法是:在分支限界开始前,先计算整个线网集S的动态界限DB(S),然后,每当得到一个新解时就检査它的值是否=DB(S),如果相等,则根据S.lt
公式(3),就可断定此解为最优,整个过程就可结束,用不到进行耗尽式的验证;如果不等,才让它继续分支限界下去。
这一措施是否有效也决定于所求界限的精确性(对 Kernighan所举例子来说本措施全部有效)。 但与倒限界法保证最优解所需条件不同,这里只要对整个集合的一次求界为精确値就可以了,这就容易得到,实际遇到的问题绝大部分能做到这一点。
5. 重排线网的次序
这一措施的目的是让最优解或较优的解尽可能地排在 判定樹上较早搜索到的那些分支上。 判定树的结沟由分支规则(左边算法) 确定。但因最左线网一般不是唯一的,因而如何分支,即先选什么线网后选什么线网,有了灵活性。这就使判定树的结构在一定程度上可以改变。本措施的具体做法是:在约束级别和静态界限求出之后,將各zone中的起始线网重新排队,使静态界限大的排在前面,如果静态界限一致,则使约束级别高的排在前面;而在进入分支限界后每次都按线网的这种先后顺序来选择下一最左线网。 (*)
------
(*)如果以双边算法为初始布线算法, 则此步骤已预先完成。
6. 寻找一种新的界限
精确的求界方法对分支限界法的快速剪枝是关键, 对上面提出的倒限界分支限界法以及最优性验证法来说则更重要。 Kernighan动态界限在一般例子中是相当精确的,但在特殊情况下有可能变差。分析其原因,在于:它考虑了线网的水平重叠关系,也考虑了它们的垂直约束关系,但没有考底在布线过程中由相互重盘的线网引起的新的垂直约束关系。例如在图7中,线网①与⑤或⑨並无约東关系,只要它们水平不重叠,就可以共行(如①与⑨)。 但是,因①②水平重量,必须放在不同行上,这样,如果①放在②上,则①也就必须在⑤⑧之上,从而使①不能与⑨共行,这就是新的约東关系。
这种新约束关系使动态界限在估算布线需要行数时有时要失敗(变小)。上例就是如此因为,①与⑨之同无约束关系且不重盘, ②与⑥之同也是这样。但在实际布线之中,这两对线网之间必有一对产生了新的约束关系,而 DB的计算中没有考慮到这种情况。
由这一例子的启发,我们可以引进一种估算布线需要行数的更精确的方法(见图12 ) : 从原来的线网集S形成两个新的线网集Sl, S2,在S1中①约束②,s2中②约束①;然后,分别计算Sl与S2的动态界限:DB(S1), DB(S2);而S的新意义下的动态界限, NDB(S), = min(DB(S1), DB(S2))。
图12
按此方法计算, S的新动念界限等于8,也即布线实际需要行数的精确下界。
但是,在一般情状下,要完整考察线网重叠引起的垂直约束是非常复杂的。必须简化才行,简化的原则就是只考察最有可能引起新约束关系的少数线网,这就是静态界限很大、约束级别最高的那些线网。
7. 快速最优通道布线算法
将上述加快措施中的一个或相容的多个加到Kernighan算法或Wada算法中去,就可得到一系列的改进算法,例如以下形式都是可取的:
(A). 在Kernighan算法加进Wada的两个加快措施后得到的改进形式基础上,再增加新的最优性验证措施。这是一个容易修改、容易得到效果而增加的工作只是一次动态界限的计算。
(B). 在(A)基础上,采用倒限界分支限界法作为初始布线算法。这一修改将使包含50个线网的布线问题在小型机上可能增加1移钟的计算时间,但由此可使分支限界过程缩短的时间有时可100倍于此。程序並不要重编,只要在原来算法基础上插入少数判别语句和执行语句就可以实现这个初始布线。
(C). 在(B)基础上采用线网重排措施。重排线网,通常可改善左边算法或倒限界法的结果,有时单独使用它就可使左边算法获得最优解。在(B)基础上再加上这一措施一般也是有益的,但对(B).本身已能获得最优结果的问题就要增加一点点运行时间,如0.l秒。
(D). 在(C)基础上,再加上新的动态界限计算方法。这一措施对“困难”间题来说会是很有益的,但对“容易的”问题则反而会因为措施本身的工作量而使计算复杂化。因此必须选择使用。选择的方法是:先计算被布集合S的动态界限DB(S),再用倒限界分支限法进行布线,若布线需要行数V与DB(S)之差≤ 1,则说明用分支限法最多只能改善1个 track,就不用新措施,否则,若大于1,就可采用它。
(E). 在(A)基础上,采用双边算法作为初始布线算法,这一形式大体和(C)一致。
(F). 在(E)基础上加上新动态界限计算方法。这一步应和(D)一样,是有选择的,选择方法类似。
IV 运行结果和讨论
以下表1是在PDP11/34小型机上对几个算法的部分运行结果,7个例子中除最后一个外,其余全部来源于[2] ,而最后一个是人为构造出来的例子,它包含50个线网,无垂直约束,有大量的可行解,这一例子用来说明采用耗尽式最优性验证法的严重缺点。
算法一共列出8个,如下:
LEA -- 左边算法,采用了分zone措施;
BEA-- 双边算法;
RBT1 -- 倒限界都分优化分支限界法,预先重排了线网;
Wada -- 即在 Kernighan的最优通道布线算法基础上,采用了Wada的两个加速措施后的改进形式;
FOA -- wada算法中加进新的最优性验证技术;
FOB -- 采用倒限界分支法作为初始布线算法的 FOA;
FOC -- 预先重排线開的FOB;
RBT2-- 倒限界完全优化的分支限界法。
程序是在分时操作系统中运行的,因而统计的时间仅可作参考。算法的效率可以从其分支和求界的次数的多少获得较精确的比较。
以双边算法为初始布线算法的快速最优布线我们没有列出来,但其结果大体可从双边算法本身的效率看出。
从表1可以看出,双边算法BEA、倒限界法RBT1是两个很好的启发式算法,它们对所有例子运行结果与最优解行数相差都不大于1 , 且大部分获得了最优解,特别是RBT1。这两个算法完全可以独立使用。
已经证明,通道布线问题是NP完备的,因此,随著大規模集成电路规模的不断扩大,采用分支限界法必然会遇到十分困难的间题,但是要看到,计算机的速度也在飞快的提高,並且,我们不一定要对整个大規模集成电路采用一次布线的方法, 而可以利用分层次通道布线。这一思想已经被许多VLSI的成功设计所证明,如〔5〕文中報导了用分层次多元胞布线方法设计了一个32位 CMOS超大規模集成电路微处理器。
表1. 各种算法对Kernighan几个例子运行结果
| 算法 |
运行结果 |
例1 |
例2 |
例3 |
例4 |
例5 |
例6 |
例7 |
|
左边算法 LEA
|
使用行数 耗时秒数 分支次数 求界次数 |
14 0.12 21 0 |
20 0.4 21 0 |
24 0.46 54 0 |
16 0.22 45 0 |
19 0.31 48 0 |
20 0.35 52 0 |
10 0.25 50 0 |
|
双边算法 BEA |
使用行数 耗时秒数 分支次数 求界次数 |
12 0.4 21 0 |
19 0.12 21 0 |
18 0.4 21 0 |
16 0.46 54 0 |
18 0.22 45 0 |
19 0.31 48 0 |
10 0.9 50 0 |
|
倒限界法 RBT |
使用行数 耗时秒数 分支次数 求界次数 |
12 0.6 23 13 |
19 2.6 63 20 |
18 8.4 128 56 |
15 1.9 93 48 |
18 2.9 79 32 |
20 2.2 52 17 |
10 1.3 50 0 |
|
最优算法 FOA |
使用行数 耗时秒数 分支次数 求界次数 |
12 0.9 37 24 |
19 43 810 635 |
17 516 14304 7205 |
15 3.9 276 167 |
17 12 571 300 |
18 21 411 220 |
10 1.3 50 0 |
|
最优算法 FOB |
使用行数 耗时秒数 分支次数 求界次数 |
12 0.7 23 13 |
19 0 0 0 |
17 276 8545 4217 |
15 2 107 57 |
17 12 553 296 |
18 6.1 57 20 |
10 1.3 50 0 |
|
最优算法 FOC |
使用行数 耗时秒数 分支次数 求界次数 |
12 0.7 23 13 |
19 3.5 60 20 |
17 223 7105 3503 |
15 1.9 93 48 |
17 11 604 308 |
18 2.2 62 17 |
10 1.3 50 0 |
|
最优算法 RBT2 |
使用行数 耗时秒数 分支次数 求界次数 |
12 0.7 23 13 |
19 3.5 63 20 |
17 224 7056 3481 |
15 1.9 93 48 |
17 11 556 289 |
18 2.2 52 17 |
10 1.3 50 0 |
|
最优算法 Wada |
使用行数 耗时秒数 分支次数 求界次数 |
12 2.5 152 112 |
19 315 10016 7025 |
17 560 14987 7560 |
15 18.5 1201 865 |
17 20 843 461 |
18 52 998 565 |
10 936 149624 130824 |
注:此表为PDP/11-34上运行结果,为尊崇历史,数据未作任何修改。
DDP,18 tracks
V. 参考文献
[1] A. Hashimoto and J.Stevens,
...“Wire Routing by Optimizing ChannelAssignment Within Large Apertures”,
....Proc. of 8thDAC,pp.155-169 (1971).
[2] B. W. Kernighan, D. G.Schweikert and G. Perskey,
....“An Optimal Channel-Routing Algorithmfor Polycell Layout of Integrated Circuits”,
....Proc. of10th DAC, pp 55-59(1973)
[3] D. N. Deutsch,
...“A Dogleg Channel Router”,
... Proc.of 13th DAC, pp 425-433 (1976).
[4] M. M. Wada,
....“A Dogleg “Optimal” Channel Routerwith Completion Enhancements”,
....Proc. ofl8th DAC, pp.762-768 (1981).
其中[2]见: