【Python 3.6】任意深度BP神经网络综合练习（非卷积网络），根据斯坦福cs231n课程编写

CIFAR10数据库
CIFAR10是一套含有60000张大小为32×32彩色RGB图像的10分类图像数据库，其中的50000张图像为训练数据，10000张图像为测试数据，另外验证集的数据从训练集中取出。

隐含层使用的激活函数：ReLU函数
输出层使用的损失函数：Softmax函数
训练集数据特征数量（即维度）：32×32×3，3表示有RGB三个色彩通道。
训练集数据量：1000个
验证集数据量：1000个
由于该案例并不专注于模型的泛化能力，而是专注于如何使用代码实现该网络，所以不需要测试集。
隐含层层数：2层
隐含层神经元数量：从第1层到第2层隐含层 100 100
初始权重矩阵的标准差：0.05
训练迭代次数：100次
每个批次的训练集数量：500个
输出层神经元数量：10，即输出10个类别
学习率：0.001
正则化系数：0.0，无正则化
学习率衰减率：无衰减
优化器：Adam
使用批量归一化

‘i_b_h’： input between hidden 输入层到第一层隐含层
‘h_b_o’：hidden between output 最后一层隐含层到输出层
‘w_h_i_b_h_i+1’：w_ith hidden between i+1th hidden 第i层隐含层到第i+1层隐含层的权重
'b_h_i_b_h_i+1：b_ith hidden between i+1th hidden 第i层隐含层到第i+1层隐含层的偏置
‘w_h_b_o’：w_hidden between output 最后一层隐含层到输出层的权重
‘b_h_b_o’ ：b_hidden between output 最后一层隐含层到输出层的偏置

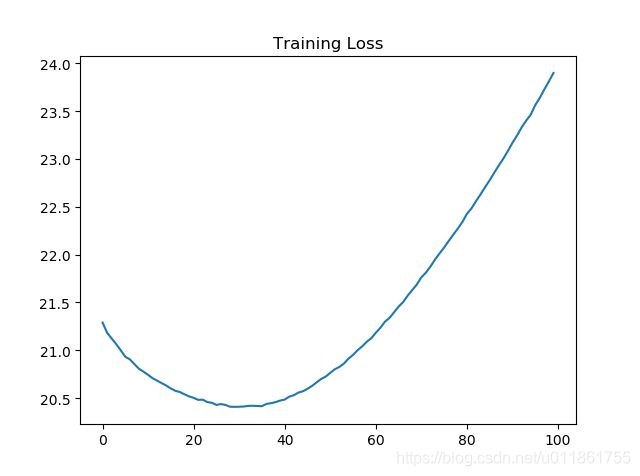
训练结果
目前存在训练损失与训练准确度共同增大的情况，，，尚不知如何解决



均已对各模块进行测试，无问题
代码

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import os
import _pickle as pickle

def rel_error(x, y):
    return np.max(np.abs(x - y) / (np.maximum(1e-8, np.abs(x) + np.abs(y))))

def eval_numerical_gradient_array(f, x, df, h=1e-5):
  """
  Evaluate a numeric gradient for a function that accepts a numpy
  array and returns a numpy array.
  """
  grad = np.zeros_like(x)
  it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
  while not it.finished:
    ix = it.multi_index
    
    oldval = x[ix]
    x[ix] = oldval + h
    pos = f(x).copy()
    x[ix] = oldval - h
    neg = f(x).copy()
    x[ix] = oldval
    
    grad[ix] = np.sum((pos - neg) * df) / (2 * h)
    it.iternext()
  return grad
    
#获取CIFAR10图像数据集
def get_CIFAR10_data(num_training=1000, num_validation=1000, num_test=0):
    cifar10_dir = 'F:/Python programs/Neural Networks/深度学习实战/cifar-10-batches-py'
    xs = []
    ys = []
    for b in range(1,6):
        f = os.path.join(cifar10_dir, 'data_batch_%d' % (b, ))
        with open(f, 'rb') as f:
            datadict = pickle.load(f, encoding = 'latin1')
            X = datadict['data']
            Y = datadict['labels']
            X = X.reshape(10000, 3, 32, 32).transpose(0,2,3,1).astype("float")
            Y = np.array(Y)
        xs.append(X)
        ys.append(Y)    
    X_train = np.concatenate(xs)
    y_train = np.concatenate(ys)
    del X, Y
    with open(os.path.join(cifar10_dir, 'test_batch'), 'rb') as f:
        datadict = pickle.load(f, encoding = 'latin1')
        X_test = datadict['data']
        y_test = datadict['labels']
        X_test = X_test.reshape(10000, 3, 32, 32).transpose(0,2,3,1).astype("float")
        y_test = np.array(y_test)
    #从原始训练集的50000张图中选出最后1000张图作为验证集
    mask = range(num_training, num_training + num_validation)
    X_val = X_train[mask]
    y_val = y_train[mask]
    mask = range(num_training)
    X_train = X_train[mask]
    y_train = y_train[mask]
    #从原始测试集中的10000张图中选出最开始的1000张图作为测试集
    mask = range(num_test)
    X_test = X_test[mask]
    y_test = y_test[mask]
    #将训练集数据进行中心化
    mean_image = np.mean(X_train, axis=0)
    X_train -= mean_image
    X_val -= mean_image
    X_test -= mean_image
    #重构尺寸
    X_train = X_train.transpose(0, 3, 1, 2).copy()
    X_val = X_val.transpose(0, 3, 1, 2).copy()
    X_test = X_test.transpose(0, 3, 1, 2).copy()
    return {
      'X_train': X_train, 'y_train': y_train,
      'X_val': X_val, 'y_val': y_val, \
      'X_test': X_test, 'y_test': y_test,
    }

#前向传播
def affine_forward(x, w, b):
    """
    计算某一层的前向传播。
    输入：x，N*D，若为RGB图像，则为N*(长*宽*3)，N为本层的神经元数量，D为特征数量
          w，D*M，M为下一层的神经元数量
          b，偏置向量，M*1
    返回：out，N*M
    """
    out = None
    #数据量
    N = x.shape[0]
    #将x整理成二维数组，N行，剩下的组成列
    x = np.reshape(x, (N,-1))
    #在数据矩阵的最后一列再添加一列1，作为偏置x0，x变成N*(D+1)
    x = np.hstack((x, np.ones((N, 1))))
    #将偏置向量b添加到权重矩阵w的最后一行，作为偏置x0的权重，w变成(D+1)*M
    w = np.vstack((w, np.transpose(b)))
    #计算下一层所有神经元对本层所有神经元的激活值，例如本层有2个神经元，下一层有3个，则输出2*3矩阵
    out = x.dot(w)
    return out

#反向传播
def affine_backward(dout, cache):
    """
    计算反向传播
    输入：
    dout，上层梯度，即残差，N*M
    cache， 上层
    输出：
    dx，输入数据的梯度，N*d1*d2*...*dk
    dw，权重矩阵的梯度，D*M
    db，偏置项b的梯度，M*1
    """
    x, w, b = cache
    dx, dw, db = None, None, None
    #反向传播
    #数据量
    N = x.shape[0]
    #将x重塑成N*D
    x = np.reshape(x, (N, -1))
    #计算残差的梯度
    dx = dout.dot(np.transpose(w))
    #计算权重的梯度
    dw = np.transpose(x)
    dw = dw.dot(dout)
    #计算偏置的梯度
    db = np.sum(dout, axis = 0)
    #将dx重塑回来
    dx = np.reshape(dx, x.shape)
    return dx, dw, db

#RelU传播
def relu_forward(x):
    """
    计算ReLUs激活函数的前向传播，然后保存结果。
    输入：
    x - 输入数据
    返回：
    out - 与输入数据的尺寸相同。
    cache - x。
    """
    out = None
    out = np.max(np.dstack((x,np.zeros(x.shape))),axis = 2)
    return out

#ReLUs反向传播
def relu_backward(dout, x):
    """
    计算ReLU函数的反向传播。
    输入：
    dout - 上层误差梯度
    x - 输入数据x
    返回：
    dx - x的梯度
    """
    dx = dout
    dx[x <= 0] = 0
    return dx

#softmax损失函数
def softmax_loss(X, y):
    """
    无正则化
    输入：
    X：神经网络的输出层激活值
    y：训练数据的标签，即真实标签
    reg：正则化惩罚系数
    输出：
    loss：损失值
    dW：权重W的梯度
    """
    #初始化损失值与梯度
    loss = 0.0
    #计算损失-------------
    #训练集数据数量N
    num_train = X.shape[0]
    #数据类别数量C
    num_catogries = X.shape[1]
    #归一化概率的分子，N*C
    #为了防止指数运算时结果太大导致溢出，这里要将X的每行减去每行的最大值
    score_fenzi = X - np.max(X, axis = 1, keepdims = True)
    score_fenzi = np.exp(score_fenzi)
    #归一化概率的分母，即，将归一化概率的分子按行求和，N*1
    score_fenmu = np.sum(score_fenzi, axis = 1, keepdims = True)
    #将分母按列复制，
    score_fenmu = score_fenmu.dot(np.ones((1, num_catogries)))
    #归一化概率，N*C/(N*1)*(1*C)=N*C/N*C
    prob = np.log(score_fenzi/score_fenmu + 1)
    y_true = np.zeros((num_train,  num_catogries))
    #把训练数据的标签铺开，例如，x是第3类，则x对应的标签为[0,0,1,0,0,0,0,0,0,0]
    y_true[range(num_train), y] = 1.0
    #y_true与p对应元素相乘后，只留下了每个数据真实标签对应的分数，例如x属于第3类，则留下第3个归一化概率
    #求出每一行归一化概率的和，即把多余的0消除，再计算所有数据归一化概率的和
    loss = -np.sum(y_true * prob) / num_train
    #计算梯度--------------
    dx = (score_fenzi/score_fenmu).copy()
    dx[np.arange(num_train), y] -= 1
    dx /= num_train
    return loss, dx

#dropout前向传播
def dropout_forward(x, param):
    """
    执行Dropout前向传播
    输入：
    x：输入数据
    dropout_param：字典类型，dropout参数
      p：dropout激活参数，每个神经元激活概率为p
      mode：'test'或'train'。train：使用激活概率p与神经元进行与运算
                             test：去除激活概率p，返回输入值
      seed：随机数生成种子
    返回：
    out：与输入数据形状相同                    
    """
    dropout_p = param['p']
    if 'seed' in param:
        np.random.seed(param['seed'])
    mask = None
    out = None
    mask = (np.random.rand(*x.shape) < dropout_p) / dropout_p
    out = x * mask
    out = out.astype(x.dtype, copy = False)
    return out, mask

#dropout反向传播
def dropout_backward(dout, mask):
     dx = None
     dx = dout * mask
     return dx
 
#SGD_Momentum优化器
def SGD_Momentum(w, dw, config = None):
    """
    随机批量、动量梯度下降方法。
    config：使用格式。
       - learning_rate：学习率
       - momentum：[0, 1]的动量学习因子，0表示不使用动量，退化为SGD
       - velocity：速度，与w和dw形状相同。
    """
    if config is None:
        config = {}
    config.setdefault('learning_rate', 1e-3)
    config.setdefault('momentum', 0.9)
    config.setdefault('velocity', np.zeros_like(w))
    next_w = None
    config['velocity'] = config['momentum'] * config['velocity'] - config['learning_rate'] * dw
    next_w = w + config['velocity']
    return next_w, config

#RMSProp优化器
def RMSProp(w, dw, config = None):
    """
    RMSProp更新器
    config字典：
        learning_rate
        decay_rate：历史累积梯度衰减因子，[0,1]
        epsilon：用于避免数值溢出
    """
    if config is None:
        config = {}
    config.setdefault('learning_rate', 1e-3)
    config.setdefault('decay_rate', 0.99)
    config.setdefault('epsilon', 1e-8)
    config.setdefault('cache', np.zeros_like(w))
    next_w = None
    config['cache'] = config['decay_rate'] * config['cache'] + (1 - config['decay_rate']) * dw ** 2
    next_w = w - config['learning_rate'] * dw / (np.sqrt(config['cache']) + config['epsilon'])
    return next_w, config

#Adam优化器
def Adam(w, dw, config = None):
    """
    Adam更新器
    config字典：
        learning_rate
        beta1：动量衰减因子
        beta2: 学习率衰减因子
        epsilon：避免数值溢出
        v：梯度衰减
        r：学习率衰减
        t：迭代次数
    """
    if config is None:
        config = {}
    config.setdefault('learning_rate', 1e-3)
    config.setdefault('beta1', 0.9)
    config.setdefault('beta2', 0.999)
    config.setdefault('epsilon', 1e-8)
    config.setdefault('r', np.zeros_like(w))
    config.setdefault('v', np.zeros_like(w))
    config.setdefault('t', 0)
    config['t'] += 1
    next_w = None
    config['v'] = config['beta1'] * config['v'] + (1 - config['beta1']) * dw
    config['r'] = config['beta2'] * config['r'] + (1 - config['beta2']) * dw ** 2
    config['vb'] = config['v'] / (1 - config['beta1'] ** (config['t']))
    config['rb'] = config['r'] / (1 - config['beta2'] ** (config['t']))
    next_w = w - config['learning_rate'] * config['vb'] / (np.sqrt(config['rb']) + config['epsilon'])
    return next_w, config

#前向BN
def BN_forward(x, bn_param):
    """
    使用类似动量衰减的运行时平均，计算总体均值与方差
    输入：
    x：输入数据(N, D)
    bn_param：字典，如下
        gamma：(D, )
        beta：(D, )
        eps：防止数据溢出
        momentum：平均衰减因子
        running_mean：运行时均值(D, )，预测时使用，训练阶段保留就好
        running_var：运行时方差(D, )，预测时使用，训练阶段保留就好
    输出：
    out：输出(N, D)
    cache：反向传播的缓存
    """
    eps = bn_param.setdefault('eps', 1e-7)
    momentum = bn_param.setdefault('momentum', 0.9)
    N, D = x.shape
    running_mean = bn_param.setdefault('running_mean', np.zeros(D, dtype = x.dtype))
    running_var = bn_param.setdefault('running_var', np.zeros(D, dtype = x.dtype))
    gamma = bn_param.setdefault('gamma', np.ones((D), dtype = x.dtype))
    beta = bn_param.setdefault('beta', np.zeros((D), dtype = x.dtype))
    out, cache = None, None    #计算均值
    mean = np.mean(x, axis = 0, keepdims = True)
    #平移为零均值
    x_mu = x - mean
    #计算方差
    var = np.sum(x_mu ** 2, axis = 0, keepdims = True) / N
    #得到标准差
    x_std = np.sqrt(var + eps)
    #数据归一化
    x_nor = x_mu / x_std
    #数据缩放与平移
    out = gamma * x_nor + beta
    #更新均值和方差
    bn_param['running_mean'] = momentum * running_mean + (1 - momentum) * mean
    bn_param['running_var'] = momentum * running_var + (1 - momentum) * var
    #保存中间结果，用于反向传播
    cache = {'bn_param': bn_param, 'x_nor': x_nor, 'x_std': x_std, 'x_mu': x_mu, 'N': N}
    return out, cache

#反向BN
def BN_backward(dout, cache):
    """
    BN反向传播
    输入：
    dout：上层梯度
    cache：前向BN的缓存
    输出：
    dx：数据梯度(N, D)
    dgamma：gamma梯度(D, )
    dbeta：beta梯度(D, )
    """
    dx, dgamma, dbeta = None, None, None 
    dbeta = np.sum(dout, axis = 0)
    dgamma = np.sum(cache['x_nor'] * dout, axis = 0)
    N = cache['N']
    dx = (1.0 / N) * cache['bn_param']['gamma'] * (cache['x_std'] ** 2 + cache['bn_param']['eps']) ** -0.5 * (N * dout - np.sum(
          dout, axis = 0) - cache['x_mu'] / (cache['x_std'] ** 2 + cache['bn_param']['eps']) * np.sum(dout * cache['x_mu'], axis = 0))
    return dx, dgamma, dbeta
    
#前向Dropout测试
x_dropout_test = np.random.randn(500, 500) + 10
out, _ = dropout_forward(x_dropout_test, {'p': 0.5})
print('前向Dropout自检-----------------------')
print('输入数据均值：', x_dropout_test.mean())
print('Dropout操作后的数据均值：', out.mean())
if rel_error(x_dropout_test.mean(), out.mean()) < 1e-3:
    print('测试通过^_^\n')
else:
    print('测试未通过')

#反向Dropout测试
x_dropout_test = np.random.randn(10, 10) + 10
dout = np.random.randn(*x_dropout_test.shape)
dropout_param = {'p': 0.8, 'seed': 123}
out, mask_test = dropout_forward(x_dropout_test, dropout_param)
dx = dropout_backward(dout, mask_test)
dx_num = eval_numerical_gradient_array(lambda xx: dropout_forward(xx, dropout_param)[0], x_dropout_test, dout)
print('反向Dropout自检-----------------------')
print('相对误差：', rel_error(dx, dx_num))
if rel_error(dx, dx_num) < 1e-10:
    print('测试通过^_^\n')
else:
    print('测试未通过\n')

#SGD_Momentum函数测试
N, D = 4, 5
w = np.linspace(-0.4, 0.6, num = N * D). reshape(N, D)
dw = np.linspace(-0.6, 0.4, num = N * D). reshape(N, D)
v = np.linspace(0.6, 0.9, num = N * D). reshape(N, D)
config_test = {'learning_rate': 1e-3, 'momentum': 0.9, 'velocity': v}
next_w, config_test = SGD_Momentum(w, dw, config = config_test)
expected_next_w = np.asarray([
    [ 0.1406,      0.20738947,  0.27417895,  0.34096842,  0.40775789],
    [ 0.47454737,  0.54133684,  0.60812632,  0.67491579,  0.74170526],
    [ 0.80849474,  0.87528421,  0.94207368,  1.00886316,  1.07565263],
    [ 1.14244211,  1.20923158,  1.27602105,  1.34281053,  1.4096    ]]),
expected_velocity = np.asarray([
    [ 0.5406,      0.55475789,  0.56891579, 0.58307368,  0.59723158],
    [ 0.61138947,  0.62554737,  0.63970526,  0.65386316,  0.66802105],
    [ 0.68217895,  0.69633684,  0.71049474,  0.72465263,  0.73881053],
    [ 0.75296842,  0.76712632,  0.78128421,  0.79544211,  0.8096    ]])
print('SGD_Momentum更新器自检---------------------')
print('更新权重误差: ', rel_error(next_w, expected_next_w))
print('速度误差: ', rel_error(expected_velocity, config_test['velocity']))
if rel_error(next_w, expected_next_w) < 1e-8 and rel_error(expected_velocity, config_test['velocity']) < 1e-8:
    print('测试通过^_^\n')
else:
    print('测试未通过\n')

#RMSProp函数测试
N, D = 4, 5
w = np.linspace(-0.4, 0.6, num = N * D). reshape(N, D)
dw = np.linspace(-0.6, 0.4, num = N * D). reshape(N, D)
cache = np.linspace(0.6, 0.9, num = N * D). reshape(N, D)
config_test = {'learning_rate': 1e-2, 'cache': cache}
next_w, config_test = RMSProp(w, dw, config = config_test)
expected_next_w = np.asarray([
    [-0.39223849, -0.34037513, -0.28849239, -0.23659121, -0.18467247],
    [-0.132737,   -0.08078555, -0.02881884,  0.02316247,  0.07515774],
    [ 0.12716641,  0.17918792,  0.23122175,  0.28326742,  0.33532447],
    [ 0.38739248,  0.43947102,  0.49155973,  0.54365823,  0.59576619]])
expected_cache = np.asarray([
    [ 0.5976,      0.6126277,   0.6277108,   0.64284931,  0.65804321],
    [ 0.67329252,  0.68859723,  0.70395734,  0.71937285,  0.73484377],
    [ 0.75037008,  0.7659518,   0.78158892,  0.79728144,  0.81302936],
    [ 0.82883269,  0.84469141,  0.86060554,  0.87657507,  0.8926    ]])
print('RMSProp更新器自检--------------------------')
print('权重更新误差：', rel_error(expected_next_w, next_w))
print('cache误差：', rel_error(expected_cache, config_test['cache']))
if rel_error(expected_next_w, next_w) < 1e-7 and rel_error(expected_cache, config_test['cache']) < 1e-7:
    print('测试通过^_^\n')
else:
    print('测试未通过\n')

#Adam函数测试
N, D = 4, 5
w = np.linspace(-0.4, 0.6, num = N * D). reshape(N, D)
dw = np.linspace(-0.6, 0.4, num = N * D). reshape(N, D)
v = np.linspace(0.6, 0.9, num = N * D). reshape(N, D)
r = np.linspace(0.7, 0.5, num = N * D). reshape(N, D)
config_test = {'learning_rate': 1e-2, 'beta1': 0.9, 'beta2': 0.999, 'epsilon': 1e-7, 'r': r, 'v': v, 't': 5}
next_w, config_test = Adam(w, dw, config = config_test)
expected_next_w = np.asarray([
    [-0.40094747, -0.34836187, -0.29577703, -0.24319299, -0.19060977],
    [-0.1380274,  -0.08544591, -0.03286534,  0.01971428,  0.0722929],
    [ 0.1248705,   0.17744702,  0.23002243,  0.28259667,  0.33516969],
    [ 0.38774145,  0.44031188,  0.49288093,  0.54544852,  0.59801459]])
expected_r = np.asarray([
    [ 0.69966,     0.68908382,  0.67851319,  0.66794809,  0.65738853,],
    [ 0.64683452,  0.63628604,  0.6257431,   0.61520571,  0.60467385,],
    [ 0.59414753,  0.58362676,  0.57311152,  0.56260183,  0.55209767,],
    [ 0.54159906,  0.53110598,  0.52061845,  0.51013645,  0.49966,   ]])
expected_v = np.asarray([
    [ 0.48,        0.49947368,  0.51894737,  0.53842105,  0.55789474],
    [ 0.57736842,  0.59684211,  0.61631579,  0.63578947,  0.65526316],
    [ 0.67473684,  0.69421053,  0.71368421,  0.73315789,  0.75263158],
    [ 0.77210526,  0.79157895,  0.81105263,  0.83052632,  0.85      ]])
print('Adam更新器自检--------------------------')
print('权重更新误差：', rel_error(expected_next_w, next_w))
print('v误差：', rel_error(expected_v, config_test['v']))
print('r误差：', rel_error(expected_r, config_test['r']))
if rel_error(expected_next_w, next_w) < 1e-6 and rel_error(expected_v, config_test['v']) < 1e-7 and rel_error(expected_r, config_test['r']) < 1e-7:
    print('测试通过^_^\n')
else:
    print('测试未通过\n')

#前向BN测试
N, D1, D2, D3 = 200, 50, 60, 3
X = np.random.randn(N, D1)
W1 = np.random.randn(D1, D2)
W2 = np.random.randn(D2, D3)
a = np.maximum(0, X.dot(W1)).dot(W2)
print('前向BN自检---------------------------------')
print("批量归一化前：")
print('均值：', a.mean(axis = 0))
print('标准差：', a.std(axis = 0))
print('批量归一化后（应该为0均值，1标准差）：')
a_norm, _ = BN_forward(a, {'gamma': np.ones(D3), 'beta': np.zeros(D3)})
print('均值：', a_norm.mean(axis = 0))
print('标准差', a_norm.std(axis = 0))
if (a_norm.mean(axis = 0) - 0.0 < 1e-10).all() and (a_norm.std(axis = 0) - 1.0 < 1e-10).all() == True:
    print('测试通过^_^\n')
else:
    print('测试未通过\n')
    
#反向BN测试
N, D = 4, 5
x = 5 * np.random.randn(N, D) + 12
gamma = np.random.randn(D)
beta = np.random.randn(D)
dout = np.random.randn(N, D)
bn_param = {'gamma': gamma, 'beta': beta}
fx = lambda x: BN_forward(x, bn_param)[0]
fg = lambda a: BN_forward(x, bn_param)[0]
fb = lambda b: BN_forward(x, bn_param)[0]
dx_num = eval_numerical_gradient_array(fx, x, dout)
da_num = eval_numerical_gradient_array(fg, gamma, dout)
db_num = eval_numerical_gradient_array(fb, beta, dout)
_, cache = BN_forward(x, bn_param)
dx, dgamma, dbeta = BN_backward(dout, cache)
print('反向BN自检-----------------------------')
print('dx误差：', rel_error(dx_num, dx))
print('dgamma误差：', rel_error(da_num, dgamma))
print('dbeta误差：', rel_error(db_num, dbeta))
if rel_error(dx_num, dx) < 1e-5 and rel_error(da_num, dgamma) < 1e-8 and rel_error(db_num, dbeta) < 1e-8:
    print('测试通过^_^\n')
else:
    print('测试未通过\n')

#导入CIFAR10数据库
#输入数据
print('输入数据...')
data = get_CIFAR10_data()
X_train = data['X_train']
y_train = data['y_train']
X_val = data['X_val']
y_val = data['y_val']
X_test = data['X_test']
y_test = data['y_test']
for k, v in data.items():
    print(f"{k}：", v.shape)
print('完成\n')

#测试含多层隐含层的神经网络-------------------------------------------------

#网络超参数设置
hidden_dim = [100, 100] #从左到右分别表示第一层到最后一层隐含层的神经元数量
hidden_layers_num = len(hidden_dim) #隐含层的层数
weight_scale = 5e-2 #初始权重矩阵中各元素的标准差
input_dim = 32*32*3 #输入数据的特征数量，即维度
num_classes = 10 #输出层神经元数量
params = {} #初始化存储有权重矩阵和偏置矩阵的字典
print("参数初始化...",  end = '')
#初始化各权重矩阵与偏置向量
#初始化从输入层到第一层隐含层的权重矩阵与偏置矩阵
params['W_i_b_h'] = np.random.randn(input_dim, hidden_dim[0]) / np.sqrt(input_dim / 2)
params['b_i_b_h'] = np.zeros(hidden_dim[0])
#初始化从第一层到最后一层隐含层之间所有的权重矩阵与偏置矩阵
for i in range(hidden_layers_num - 1):
    if hidden_layers_num == 1:
        break;
    params['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = np.random.randn(hidden_dim[i], hidden_dim[i + 1]) / np.sqrt(hidden_dim[i] / 2)
    params['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = np.zeros(hidden_dim[i + 1])
#初始化从最后一层隐含层到输出层的权重矩阵与偏置矩阵
params['W_h_b_o'] = np.random.randn(hidden_dim[-1], num_classes) / np.sqrt(hidden_dim[-1] / 2)
params['b_h_b_o'] = np.zeros(num_classes)
#初始化dropout的掩模矩阵字典
dropout_mask = {}

#输入训练超参数
num_iters = 100 #迭代次数
batch_size = 500 #每一次迭代中从训练集中随机选取的数据量，选取出来作为一个批次
dropout_param = {'p': 0.7} #Dropout参数
learning_rate = 1e-3 #学习率
verbose = True #是否在命令行显示训练消息
reg = 0.0 #正则化系数
learning_rate_decay = 1.0 #学习率衰减率
iterations_per_epoch = max(X_train.shape[0] / batch_size, 1) #遍历整个训练集需要多少个批次
#可以选择的更新器：Original, Momentum, RMSProp, Adam
optimizer = 'Adam'
#存储历次迭代的损失值、训练准确率与验证准确率
loss_history = [] #历次损失值
train_history = [] #历次训练准确率
val_history = [] #历次验证准确率
#存储每次迭代生成的权重梯度与偏置梯度的字典
grad = {}
forward_out = {}
#BN传播初始化
bn_param = {}
gamma = {}
beta = {}
#Momentum、RMSProp、Adam更新器参数，BN的gamma和beta初始化
config = {'W_i_b_h': None, 'W_h_b_o': None, 'b_i_b_h': None, 'b_h_b_o': None, 'gamma_i_b_h': None, 'beta_i_b_h': None}
gamma['i_b_h'] = np.ones(hidden_dim[0])
beta['i_b_h'] = np.zeros(hidden_dim[0])
bn_dgamma = {}
bn_dbeta = {}
bn_cache = {}
for i in range(hidden_layers_num - 1):
    config['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = None
    config['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = None
    config['gamma_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = None
    config['beta_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = None
    gamma['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = np.ones(hidden_dim[i + 1])
    beta['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = np.zeros(hidden_dim[i + 1])
print('完成\n')


print('开始训练')
#开始训练
for it in range(num_iters):
    num_train = X_train.shape[0] #训练集中的总数据量
    X_batch = None
    y_batch = None
    #从训练集中随机取出batch_size个训练数据
    #从0到num_train-1中随机取batch_size个数字，作为一个批次的训练数据的索引
    i = np.random.choice(range(num_train), batch_size, replace = False)
    X_batch = X_train[i,:]
    #标签y和训练数据X必须对应，例如取出了第3个数据，则必须取出第3个标签
    y_batch = y_train[i]
    #前向传播------------------------
    #从输入层传到第一层隐含层
    #前向仿射变换
    forward_out_i2h = affine_forward(X_batch, params['W_i_b_h'], params['b_i_b_h'])
    #前向批量归一化
    forward_out_i2h, bn_cache['i_b_h'] = BN_forward(forward_out_i2h, {'gamma': gamma['i_b_h'], 'beta': beta['i_b_h']})
    #前向ReLU激活
    forward_out['i2h'] = relu_forward(forward_out_i2h)
    #前向Dropout
    forward_out['i2h'], dropout_mask['i2h'] = dropout_forward(forward_out['i2h'], dropout_param)
    #从第二层隐含层到最后一层隐含层
    if hidden_layers_num > 1:
        for i in range(hidden_layers_num - 1):
            if i == 0:
                forward_out['h' + str(i) + '_2_' + 'h' + str(i + 1)] = forward_out['i2h']
            #前向仿射变换
            forward_out['h' + str(i + 1) + '_2_' + 'h' + str(i + 2)] = affine_forward(forward_out['h' + str(i) + '_2_' + 'h' + str(i + 1)], 
                                                params['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                                params['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)])
            #前向批量归一化
            forward_out['h' + str(i + 1) + '_2_' + 'h' + str(i + 2)], bn_cache['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = BN_forward(forward_out['h' + str(i + 1) + '_2_' + 'h' + str(i + 2)], 
                                  {'gamma': gamma['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 'beta': beta['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)]})
            #前向ReLU激活
            forward_out['h' + str(i + 1) + '_2_' + 'h' + str(i + 2)] = relu_forward(forward_out['h' + str(i + 1) + '_2_' + 'h' + str(i + 2)])
            #前向Dropout
            forward_out['h' + str(i + 1) + '_2_' + 'h' + str(i + 2)], dropout_mask['h' + str(i + 1) + '_2_' + 'h' + str(i + 2)] = dropout_forward(forward_out['h' + str(i + 1) + '_2_' + 'h' + str(i + 2)], dropout_param)
        forward_out_hidden = forward_out['h' + str(hidden_layers_num - 1) + '_2_' + 'h' + str(hidden_layers_num)]
    else:
        forward_out_hidden = forward_out['i2h']
    #从最后一层隐含层到输出层
    scores = affine_forward(forward_out_hidden, params['W_h_b_o'], params['b_h_b_o'])
    #在输出层使用softmax损失函数，计算网络的总损失与梯度
    loss, grad_out = softmax_loss(scores, y_batch)
    #对总损失加入正则项
    loss += 0.5 * reg * np.sum(params['W_i_b_h'] ** 2) + np.sum(params['W_h_b_o'] ** 2)
    for i in range(hidden_layers_num - 1):
        loss += 0.5 * reg * (np.sum(params['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] ** 2))
    #存储损失值
    loss_history.append(loss)
    #反向传播-------------------------------------------------------------------
    #计算输出层到最后一层隐含层的残差、权重梯度与偏置梯度
    dx, grad['W_o_b_h'], grad['b_o_b_h'] = affine_backward(grad_out, (forward_out_hidden, params['W_h_b_o'], params['b_h_b_o']))
    #对输出层到隐含层的权重梯度加入正则项
    grad['W_o_b_h'] += reg * params['W_h_b_o']
    #从最后一层隐含层到第一层隐含层的所有残差、权重梯度与偏置梯度
    if hidden_layers_num > 1:
        for i in range(hidden_layers_num - 1, 0, -1):
            if i == hidden_layers_num - 1:
                forward_out['h' + str(i + 1) + '_2_' + 'h' + str(i + 2)] = forward_out_hidden
            #计算第i+1层到第i层隐含层的残差、权重梯度与偏置梯度
            #反向Dropout
            dx = dropout_backward(dx, dropout_mask['h' + str(i) + '_2_' + 'h' + str(i + 1)])
            #反向ReLU
            dx = relu_backward(dx, forward_out['h' + str(i + 1) + '_2_' + 'h' + str(i + 2)])
            #反向批量归一化
            dx, bn_dgamma['h' + str(i) + '_b_' + 'h' + str(i + 1)], bn_dbeta['h' + str(i) + '_b_' + 'h' + str(i + 1)] = BN_backward(dx, bn_cache['h' + str(i) + '_b_' + 'h' + str(i + 1)])
            #反向传播
            dx, grad['W_h' + str(i + 1) + '_b_' + 'h' + str(i)], grad['b_h' + str(i + 1) + '_b_' + 'h' + str(i)] = affine_backward(dx, 
                                (forward_out['h' + str(i - 1) + '_2_' + 'h' + str(i)], 
                                 params['W_h' + str(i) + '_b_' + 'h' + str(i + 1)], 
                                 params['b_h' + str(i) + '_b_' + 'h' + str(i + 1)]))
            #对第i+1层到第i层隐含层的权重梯度加入正则项
            grad['W_h' + str(i + 1) + '_b_' + 'h' + str(i)] += reg * params['W_h' + str(i) + '_b_' + 'h' + str(i + 1)]
        forward_relu_out = forward_out['h' + str(0) + '_2_' + 'h' + str(1)]
    else:
        forward_relu_out = forward_out_hidden
    #计算第一层隐含层到输入层的残差、权重梯度与偏置梯度
    #反向Dropout
    dx = dropout_backward(dx, dropout_mask['i2h'])
    #反向ReLU
    dx = relu_backward(dx, forward_relu_out)
    #反向批量归一化
    dx, bn_dgamma['i_b_h'], bn_dbeta['i_b_h'] = BN_backward(dx, bn_cache['i_b_h'])
    dx, grad['W_h_b_i'], grad['b_h_b_i'] = affine_backward(dx, (X_batch, params['W_i_b_h'], params['b_i_b_h']))
    #对第第一层隐含层到输入层的权重梯度加入正则项
    grad['W_h_b_i'] += reg * params['W_i_b_h']
    #反向传播完成，此时回到了输入层
    #通过梯度和学习率更新权重与偏置
    #先更新输入层与第一层隐含层之间的权重和偏置，与，最后一层隐含层与输出层之间的权重和偏置
    if optimizer is 'Original':
        params['W_i_b_h'] -= learning_rate * grad['W_h_b_i']
        params['W_h_b_o'] -= learning_rate * grad['W_o_b_h']
        params['b_i_b_h'] -= learning_rate * grad['b_h_b_i']
        params['b_h_b_o'] -= learning_rate * grad['b_o_b_h']
        gamma['i_b_h'] -= learning_rate * bn_dgamma['i_b_h']
        beta['i_b_h'] -= learning_rate * bn_dbeta['i_b_h']
        learning_rate *= learning_rate_decay
    elif optimizer is 'Momentum':
        params['W_i_b_h'], config['W_i_b_h'] = SGD_Momentum(params['W_i_b_h'], grad['W_h_b_i'], config['W_i_b_h'])
        params['W_h_b_o'], config['W_h_b_o'] = SGD_Momentum(params['W_h_b_o'], grad['W_o_b_h'], config['W_h_b_o'])
        params['b_i_b_h'], config['b_i_b_h'] = SGD_Momentum(params['b_i_b_h'], grad['b_h_b_i'], config['b_i_b_h'])
        params['b_h_b_o'], config['b_h_b_o'] = SGD_Momentum(params['b_h_b_o'], grad['b_o_b_h'], config['b_h_b_o'])
        gamma['i_b_h'], config['gamma_i_b_h'] = SGD_Momentum(gamma['i_b_h'], bn_dgamma['i_b_h'], config['gamma_i_b_h'])
        beta['i_b_h'], config['beta_i_b_h'] = SGD_Momentum(beta['i_b_h'], bn_dbeta['i_b_h'], config['beta_i_b_h'])
    elif optimizer is 'RMSProp':
        params['W_i_b_h'], config['W_i_b_h'] = RMSProp(params['W_i_b_h'], grad['W_h_b_i'], config['W_i_b_h'])
        params['W_h_b_o'], config['W_h_b_o'] = RMSProp(params['W_h_b_o'], grad['W_o_b_h'], config['W_h_b_o'])
        params['b_i_b_h'], config['b_i_b_h'] = RMSProp(params['b_i_b_h'], grad['b_h_b_i'], config['b_i_b_h'])
        params['b_h_b_o'], config['b_h_b_o'] = RMSProp(params['b_h_b_o'], grad['b_o_b_h'], config['b_h_b_o'])
        gamma['i_b_h'], config['gamma_i_b_h'] = RMSProp(gamma['i_b_h'], bn_dgamma['i_b_h'], config['gamma_i_b_h'])
        beta['i_b_h'], config['beta_i_b_h'] = RMSProp(beta['i_b_h'], bn_dbeta['i_b_h'], config['beta_i_b_h'])
    elif optimizer is 'Adam':
        params['W_i_b_h'], config['W_i_b_h'] = Adam(params['W_i_b_h'], grad['W_h_b_i'], config['W_i_b_h'])
        params['W_h_b_o'], config['W_h_b_o'] = Adam(params['W_h_b_o'], grad['W_o_b_h'], config['W_h_b_o'])
        params['b_i_b_h'], config['b_i_b_h'] = Adam(params['b_i_b_h'], grad['b_h_b_i'], config['b_i_b_h'])
        params['b_h_b_o'], config['b_h_b_o'] = Adam(params['b_h_b_o'], grad['b_o_b_h'], config['b_h_b_o'])
        gamma['i_b_h'], config['gamma_i_b_h'] = Adam(gamma['i_b_h'], bn_dgamma['i_b_h'], config['gamma_i_b_h'])
        beta['i_b_h'], config['beta_i_b_h'] = Adam(beta['i_b_h'], bn_dbeta['i_b_h'], config['beta_i_b_h'])
    #如果隐含层数量大于1层，则再更新从第一层隐含层到最后一层隐含层之间的权重和偏置
    if hidden_layers_num > 1:
        if optimizer is 'Original':
            for i in range(hidden_layers_num - 1):
                params['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] -= learning_rate * grad['W_h' + str(i + 2) + '_b_' + 'h' + str(i + 1)]
                params['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] -= learning_rate * grad['b_h' + str(i + 2) + '_b_' + 'h' + str(i + 1)]
                gamma['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] -= learning_rate * bn_dgamma['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)]
                beta['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] -= learning_rate * bn_dbeta['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)]
            learning_rate *= learning_rate_decay
        elif optimizer is 'Momentum':
            for i in range(hidden_layers_num - 1):
                params['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], config['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = SGD_Momentum(params['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 grad['W_h' + str(i + 2) + '_b_' + 'h' + str(i + 1)], 
                                 config['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)])
                params['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], config['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = SGD_Momentum(params['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 grad['b_h' + str(i + 2) + '_b_' + 'h' + str(i + 1)], 
                                 config['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)])
                gamma['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], config['gamma_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = SGD_Momentum(beta['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 bn_dgamma['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 config['gamma_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)])
                beta['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], config['gamma_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = SGD_Momentum(gamma['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 bn_dbeta['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 config['beta_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)])
        elif optimizer is 'RMSProp':
            for i in range(hidden_layers_num - 1):
                params['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], config['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = RMSProp(params['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 grad['W_h' + str(i + 2) + '_b_' + 'h' + str(i + 1)], 
                                 config['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)])
                params['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], config['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = RMSProp(params['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 grad['b_h' + str(i + 2) + '_b_' + 'h' + str(i + 1)], 
                                 config['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)])
                gamma['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], config['gamma_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = RMSProp(gamma['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 bn_dgamma['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 config['gamma_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)])
                beta['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], config['beta_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = RMSProp(beta['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 bn_dbeta['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 config['beta_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)])
        elif optimizer is 'Adam':
            for i in range(hidden_layers_num - 1):
                params['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], config['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = Adam(params['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 grad['W_h' + str(i + 2) + '_b_' + 'h' + str(i + 1)], 
                                 config['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)])
                params['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], config['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = Adam(params['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 grad['b_h' + str(i + 2) + '_b_' + 'h' + str(i + 1)], 
                                 config['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)])
                gamma['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], config['gamma_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = Adam(gamma['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 bn_dgamma['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 config['gamma_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)])
                beta['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], config['beta_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] = Adam(beta['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 bn_dbeta['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                 config['beta_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)])
    if verbose == True:
        print(f"第{it}/{num_iters}次迭代，损失为{loss}，", end = '\n')
    if it % iterations_per_epoch == 0:
        #做一个预测，计算此次迭代的训练准确率、验证准确率
        #计算训练准确率
        pred_out = affine_forward(X_batch, params['W_i_b_h'], params['b_i_b_h'])
        pred_out = (pred_out - bn_cache['i_b_h']['bn_param']['running_mean']) / np.sqrt(bn_cache['i_b_h']['bn_param']['running_var'])
        pred_out = gamma['i_b_h'] * pred_out + beta['i_b_h']
        pred_out = relu_forward(pred_out)
        if hidden_layers_num > 1:
            for i in range(hidden_layers_num - 1):
                pred_out = affine_forward(pred_out, 
                                          params['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                          params['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], )
                pred_out = (pred_out - bn_cache['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)]['bn_param']['running_mean']) / \
                                          np.sqrt(bn_cache['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)]['bn_param']['running_var'])
                pred_out = gamma['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] * pred_out + beta['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)]
                pred_out = relu_forward(pred_out)
        pred_out = affine_forward(pred_out, params['W_h_b_o'], params['b_h_b_o'])
        pred_out = np.argmax(pred_out, axis = 1)
        train_acc = np.mean(pred_out == y_batch)
        train_history.append(train_acc)
        #计算验证准确率
        valpred_out = affine_forward(X_val, params['W_i_b_h'], params['b_i_b_h'])
        valpred_out = (valpred_out - bn_cache['i_b_h']['bn_param']['running_mean']) / np.sqrt(bn_cache['i_b_h']['bn_param']['running_var'])
        valpred_out = gamma['i_b_h'] * valpred_out + beta['i_b_h']
        valpred_out = relu_forward(valpred_out)
        if hidden_layers_num > 1:
            for i in range(hidden_layers_num - 1):
                valpred_out = affine_forward(valpred_out, 
                                          params['W_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], 
                                          params['b_h' + str(i + 1) + '_b_' + 'h' + str(i + 2)], )
                valpred_out = (valpred_out - bn_cache['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)]['bn_param']['running_mean']) / \
                                          np.sqrt(bn_cache['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)]['bn_param']['running_var'])
                valpred_out = gamma['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)] * valpred_out + beta['h' + str(i + 1) + '_b_' + 'h' + str(i + 2)]
                valpred_out = relu_forward(valpred_out)
        valpred_out = affine_forward(valpred_out, params['W_h_b_o'], params['b_h_b_o'])
        valpred_out = np.argmax(valpred_out, axis = 1)
        val_acc = np.mean(valpred_out == y_val)
        val_history.append(val_acc)
        print(f'训练准确度为{train_acc}, 验证准确度为{val_acc}')
    
#结果显示
plt.figure(1)
plt.plot(loss_history)
plt.title('Training Loss')
plt.figure(2)
plt.plot(train_history, label = 'Training Accuracy')
plt.legend()
plt.title('Accuracy')
plt.plot(val_history, label = 'Validation Accuracy')
plt.legend()