专题练习——回溯
文章目录
- 回溯框架
- 一、LeetCode77. 组合
- 题目描述
- 方法一、回溯
- 方法二、回溯+剪枝
- 二、LeetCode78. 子集
- 题目描述
- 方法一、回溯
- 方法二、枚举法
- 三、LeetCode46. 全排列
- 题目描述
- 方法一、回溯法
- 方法二、递归,元素交换实现
- 四、LeetCode47. 全排列 II
- 题目描述
- 递归,元素交换实现
- 五、LeetCode17. 电话号码的字母组合
- 题目描述
- 方法一、回溯法
- 方法二、用队列解
- 六、LeetCode51. N皇后
- 题目描述
- 回溯法
- 七、LeetCode52. N皇后 II
- 题目描述
- 回溯法(稍微修改上一题代码)
回溯框架
回溯法是所有搜索算法中最为基本的一种算法,又称为试探法,基本做法是深度优先搜索。
回溯算法框架如下所示,其核心就是 for 循环里面的递归,在递归调⽤之前做出选择,在递归调⽤之后撤销该选择。
result = []
function backtrack(路径, 选择列表) {
if (满足条件) { // 结束条件
result.add(路径);
return;
}
for (选择 in 选择列表) {
做出选择
backtrack(路径,选择列表)
撤销选择
}
}
一、LeetCode77. 组合
题目描述
链接
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
方法一、回溯
这里用了一个begin防止搜索重复的值
class Solution {
public List<List<Integer>> list = new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
if (n <= 0 || k <= 0 || n < k)
return list;
backTrack(n, k, 1, new Stack<>());
return list;
}
private void backTrack(int n, int k, int begin, Stack<Integer> track) {
//结束条件
if (track.size() == k) {
list.add(new ArrayList<>(track));
return;
}
for(int i = begin; i <= n; i++){
track.push(i); //做出选择
backTrack(n, k, i + 1, track);
track.pop(); //撤销选择
}
}
}
方法二、回溯+剪枝
设想一下从[1,2,3,4,5]中取出3个数,for循环到3的时候,还刚好剩下3个数,但循环到4时,以及不够3个数了,这些分支是没必要执行的。
class Solution {
public List<List<Integer>> list = new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
if (n <= 0 || k <= 0 || n < k)
return list;
backTrack(n, k, 1, new Stack<>());
return list;
}
private void backTrack(int n, int k, int begin, Stack<Integer> track) {
//结束条件
if (track.size() == k) {
list.add(new ArrayList<>(track));
return;
}
/*
//剪枝:剩下的个数不足时,停止搜索
// i 的极限值满足: n - i + 1 = (k - track.size())。
// n - i + 1 是 [i,n] 的长度。
// k - track.size() 是剩下还要寻找的数的个数。
*/
for(int i = begin; i <= n - (k - track.size()) + 1; i++){
track.push(i); //做出选择
backTrack(n, k, i + 1, track);
track.pop(); //撤销选择
}
}
}
二、LeetCode78. 子集
题目描述
链接
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
方法一、回溯
class Solution {
public List<List<Integer>> list = new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {
backTrack(nums, 0, new Stack<Integer>());
return list;
}
private void backTrack(int[] nums, int begin, Stack<Integer> track) {
list.add(new ArrayList<>(track));
for (int i = begin; i < nums.length; i++) {
track.push(nums[i]);
backTrack(nums, i + 1, track);
track.pop();
}
}
}
方法二、枚举法
逐个枚举,空集的幂集只有空集,每增加一个元素,让之前幂集中的每个集合,追加这个元素,就是新增的子集。
比如说:1,2,3的子集
- 首先,添加一个空List到结果List(res)中
- for循环遍历到1,[]加上1,添加到res中,此时res:[ [] , [1] ]
- for循环遍历到2,res中每个list都加上2,此时res:[ [] , [1] , [2] , [1,2] ]
- for循环遍历到3,res中每个list都加上3,此时res:[ [] , [1] , [2] , [1,2] , [3] , [1,3] , [2,3] , [1,2,3]]
class Solution {
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> res = new ArrayList();
res.add(new ArrayList<Integer>());//添加空白元素
for (Integer num : nums) {
int size = res.size();
for (int i = 0; i < size; i++) {
List<Integer> newSub = new ArrayList<>(res.get(i));
newSub.add(num);
res.add(newSub);
}
}
return res;
}
}
三、LeetCode46. 全排列
题目描述
链接
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
方法一、回溯法
class Solution {
public List<List<Integer>> list = new LinkedList<>();
public List<List<Integer>> permute(int[] nums) {
backTrack(nums, new LinkedList<>());
return list;
}
private void backTrack(int[] nums, LinkedList<Integer> track) {
//结束条件
if (track.size() == nums.length) {
list.add(new LinkedList(track));
return;
}
//选择列表
for (int i = 0; i < nums.length; i++) {
//排除不合理的选择
if (track.contains(nums[i]))
continue;
//做出选择
track.add(nums[i]);
//进入下一层决策树
backTrack(nums, track);
//撤销选择
track.removeLast();
}
}
}
方法二、递归,元素交换实现
class Solution {
public List<List<Integer>> list = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
backTrack(nums, 0);
return list;
}
private void backTrack(int[] nums, int start) {
//结束条件
if (start == nums.length) {
List<Integer> curr = Arrays.stream(nums).boxed().collect(Collectors.toList());//将数组转换为List
list.add(curr);
}
//选择列表
for (int i = start; i < nums.length; i++) {
//交换
int temp = nums[i];
nums[i] = nums[start];
nums[start] = temp;
//进入下一层决策树
backTrack(nums, start + 1);
//交换回来(撤销之前的交换)
temp = nums[i];
nums[i] = nums[start];
nums[start] = temp;
}
}
}
四、LeetCode47. 全排列 II
题目描述
添加链接描述链接
给定一个可包含重复数字的序列,返回所有不重复的全排列。
示例:
输入: [1,1,2]
输出:
[
[1,1,2],
[1,2,1],
[2,1,1]
]
递归,元素交换实现
在上一题的方法二的基础上,添加了一个HashSet去重。
class Solution {
public List<List<Integer>> list = new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
backTrack(nums, 0);
return list;
}
private void backTrack(int[] nums, int start) {
//结束条件
if (start == nums.length) {
List<Integer> curr = Arrays.stream(nums).boxed().collect(Collectors.toList());//将数组转换为List
list.add(curr);
}
//选择列表
HashSet<Integer> set = new HashSet<>();
for (int i = start; i < nums.length; i++) {
//去重
if(set.contains(nums[i]))
continue;
set.add(nums[i]);
//交换
int temp = nums[i];
nums[i] = nums[start];
nums[start] = temp;
//进入下一层决策树
backTrack(nums, start + 1);
//交换回来(撤销之前的交换)
temp = nums[i];
nums[i] = nums[start];
nums[start] = temp;
}
}
}
五、LeetCode17. 电话号码的字母组合
题目描述
链接
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例:
输入:"23"
输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
方法一、回溯法
class Solution {
private Map<Character, String> phone = new HashMap<>() {{
put('2', "abc");
put('3', "def");
put('4', "ghi");
put('5', "jkl");
put('6', "mno");
put('7', "pqrs");
put('8', "tuv");
put('9', "wxyz");
}};
private List<String> res = new ArrayList<String>();
public List<String> letterCombinations(String digits) {
if (digits == null || digits.length() == 0){
return res;
}
backTrack(new StringBuilder(), 0, digits);
return res;
}
private void backTrack(StringBuilder combination, int index, String digits) {
//结束条件
if (index == digits.length()) {
res.add(combination.toString());
return;
}
//选择列表
String currNumChar = phone.get(digits.charAt(index));//index位置的数字所代表的字符序列
for (int i = 0; i < currNumChar.length(); i++) {
//做出选择
combination.append(currNumChar.charAt(i));
//进入下一层决策树
backTrack(combination, index + 1, digits);
//撤销选择
combination.deleteCharAt(combination.length() - 1);
}
}
}
方法二、用队列解
利用队列先进先出的特点,每次从队列中取出一个元素与新数字所代表的的每一个字符进行拼接并入队。
比如说输入为“23”:
- 初始队列为空,把“”依次和数字2所代表的“abc”拼接,得到队列[a,b,c]
- 对于队列[a,b,c],依次和数字3所代表的的“def”拼接:
– 取出a,与def拼接,得到队列[b,c,ad,ae,af]
– 取出b,与def拼接,得到队列[c,ad,ae,af,bd,be,bf]
– 取出c,与def拼接,得到队列[ad,ae,af,bd,be,bf,cd,ce,cf].
class Solution {
private Map<Character, String> phone = new HashMap<>() {{
put('2', "abc");
put('3', "def");
put('4', "ghi");
put('5', "jkl");
put('6', "mno");
put('7', "pqrs");
put('8', "tuv");
put('9', "wxyz");
}};
public List<String> letterCombinations(String digits) {
List<String> res = new ArrayList<String>();
if (digits == null || digits.length() == 0){
return res;
}
res.add("");
for (int i = 0; i < digits.length(); i++) {
String currNumChar = phone.get(digits.charAt(i));//获取当前数字代表的字符序列
int size = res.size();
for (int j = 0; j < size; j++) {//取出队列中每一个元素,与当前数字代表的每一个字符拼接
String letter = res.remove(0);//取出第一个字符串
//并分别和当前数字所代表的的字符串中的每一个字符进行拼接
for (int k = 0 ; k < currNumChar.length(); k++) {
res.add(letter + currNumChar.charAt(k));
}
}
}
return res;
}
}
六、LeetCode51. N皇后
题目描述
链接
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
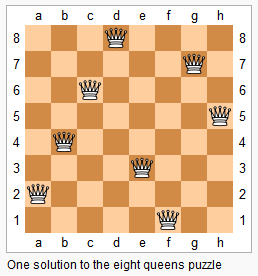
输出:
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。
提示:
皇后,是国际象棋中的棋子,意味着国王的妻子。皇后只做一件事,那就是“吃子”。当她遇见可以吃的棋子时,就迅速冲上去吃掉棋子。当然,她横、竖、斜都可走一到七步,可进可退。(引用自 百度百科 - 皇后 )
回溯法
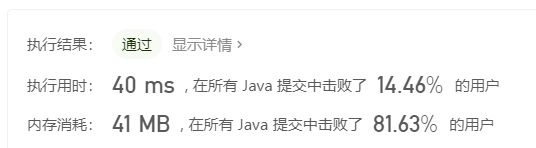
LeetCode提交时间为8ms
class Solution {
private List<List<String>> res = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
if (n < 1)
return res;
List<String> board = new ArrayList<>();
StringBuilder sb = new StringBuilder();
for (int i = 0; i < n; i++)
sb.append('.');
for (int i = 0; i < n; i++)
board.add(sb.toString());
backTrack(n, 0, board);
return res;
}
private void backTrack(int n, int row, List<String> board) {
//结束条件
if (row >= n) {
res.add(new ArrayList<>(board));
return;
}
//选择列表:当前层的每一列
for (int col = 0; col < n; col++) {
//排除不合法的选择
if (!isValid(board, row, col, n)) {
continue;
}
//做选择
StringBuilder sb = new StringBuilder(board.get(row));
sb.setCharAt(col, 'Q');
board.set(row, sb.toString());
//进入下一层决策树
backTrack(n, row + 1, board);
//撤销选择
sb = new StringBuilder(board.get(row));
sb.setCharAt(col, '.');
board.set(row, sb.toString());
}
}
private boolean isValid(List<String> board, int row, int col, int n) {
//检查同一列有没有冲突
for (int i = 0; i < row; i++) {
if (board.get(i).charAt(col) == 'Q')
return false;
}
//检查\列有没有冲突
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (board.get(i).charAt(j) == 'Q')
return false;
}
//检查/列有没有冲突
for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (board.get(i).charAt(j) == 'Q')
return false;
}
return true;
}
}
进行代码优化,仅适用2ms:
public class Solution {
private boolean[] visited;
private boolean[] dia1;
private boolean[] dia2;
private List<List<String>> res = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
visited = new boolean[n];
//2*n-1个斜对角线
dia1 = new boolean[2*n-1];
dia2 = new boolean[2*n-1];
backTrack(new ArrayList<String>(), 0, n);
return res;
}
private void backTrack(List<String> list, int row, int n){
//结束条件
if (row == n){
res.add(new ArrayList<String>(list));
return;
}
for (int i = 0; i < n; i++){
//排除不合法的选择
if (visited[i] || dia1[row+i] || dia2[row-i+n-1])
continue;
//做选择
char[] charArray = new char[n];
Arrays.fill(charArray, '.');
charArray[i] = 'Q';
String rowString = new String(charArray);
list.add(rowString);
visited[i] = true;
dia1[row+i] = true;// "/",row+col用来标识一条“/”
dia2[row-i+n-1] = true;// "\",row-col用来标识一条“\”,+n-1是为了防止数组越界
//进入下一层决策树
backTrack(list, row + 1, n);
//撤销选择
list.remove(list.size() - 1);
charArray[i] = '.';
visited[i] = false;
dia1[row+i] = false;
dia2[row-i+n-1] = false;
}
}
}
七、LeetCode52. N皇后 II
题目描述
链接
给定一个整数 n,返回 n 皇后不同的解决方案的数量。
回溯法(稍微修改上一题代码)
class Solution {
private int count = 0;
public int totalNQueens(int n) {
if (n < 1)
return count;
List<String> board = new ArrayList<>();
StringBuilder sb = new StringBuilder();
for (int i = 0; i < n; i++)
sb.append('.');
for (int i = 0; i < n; i++)
board.add(sb.toString());
backTrack(n, 0, board);
return count;
}
private void backTrack(int n, int row, List<String> board) {
//结束条件
if (row >= n) {
count++;
return;
}
//选择列表:当前层的每一列
for (int col = 0; col < n; col++) {
//排除不合法的选择
if (!isValid(board, row, col, n)) {
continue;
}
//做选择
StringBuilder sb = new StringBuilder(board.get(row));
sb.setCharAt(col, 'Q');
board.set(row, sb.toString());
//进入下一层决策树
backTrack(n, row + 1, board);
//撤销选择
sb = new StringBuilder(board.get(row));
sb.setCharAt(col, '.');
board.set(row, sb.toString());
}
}
private boolean isValid(List<String> board, int row, int col, int n) {
//检查同一列有没有冲突
for (int i = 0; i < row; i++) {
if (board.get(i).charAt(col) == 'Q')
return false;
}
//检查\列有没有冲突
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (board.get(i).charAt(j) == 'Q')
return false;
}
//检查/列有没有冲突
for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (board.get(i).charAt(j) == 'Q')
return false;
}
return true;
}
}