SIFT算法系列之描述符

SIFT算法描述符简述

　　SIFT算法系列一直想把描述符阶段给写完，怪自己有点小偷懒，出来混迟早要还的。这次在之前SIFT算法系列之尺度空间与SIFT算法系列之特征点检测基础上，继续完善将描述符如何生成过程写完。

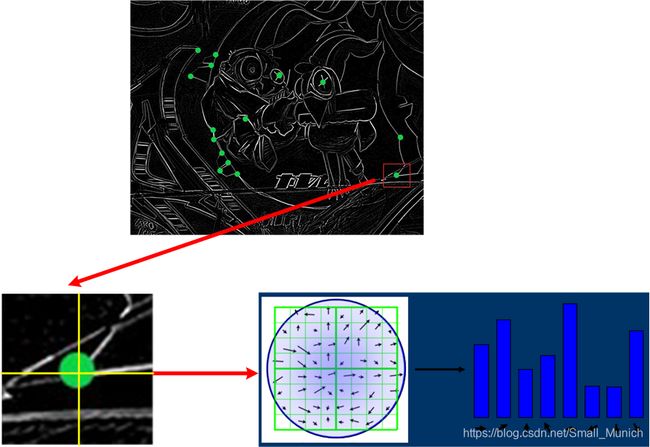
废话不多说，我们知道描述符生成是建立在特征点之后的，假设我们检测出一些特征点，如下图：

如上图，在特征点已经检测出来基础上，来计算特征点的主方向；

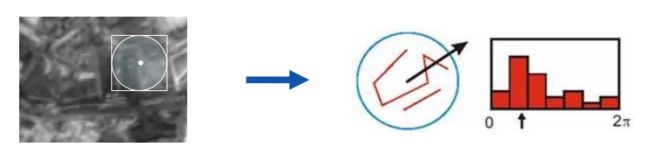
　　SIFT源代码中计算主方向：以关键点为中心对齐周围邻域窗口进行采样，首先采取高斯函数进行平滑，减少邻域像素突变干扰。然后计算邻域的像素与关键点的梯度幅值与方向来统计形成直方图。

　　梯度直方图的范围是0~360度，每45度一个柱，总共8个柱；或者设置每10度一个柱，总共36个柱。下图为8个柱示例图：

　　梯度直方图最大峰值则设置成关键点的主方向，如果第二峰值是第一峰值80%则也保存作为候选关键点辅助方向。

SIFT算法描述符构建过程

1. 确定关键点主方向后，根据关键点的尺度系数得到ROI邻域半径；

2. 将关键点邻域半径的ROI进行主方向旋转；

3. 对旋转后的ROI区域计算关键点的梯度直方图；

4. 对每个2x2的小子区域8为向量排序，生成128维向量；

5. 对128维向量进行归一化操作；

　　1 关键点的主方向确定后，首先将当前特征点尺度计算出ROI区域半径：(我们知道特征点检测会在尺度空间上进行，那么检测出来的特征点也会存在不同的尺度参数，所以我们在构建局部描述符时候需要根据不同的尺度那划分不同半径区域，这样才可以保持尺度不变性匹配)。

$$radius=\frac{(3{\sigma }_{oct}\times \sqrt{2}\times (d+1)+1)}{2}$$

其中${\sigma }_{oct}$即是尺度参数，$d=4$。

　　2 根据主方向将确定后的ROI(尺度参数来确定邻域半径)旋转至主方向：

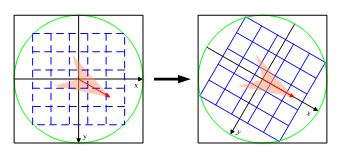
这样经过旋转后每个像素新坐标如下：

$$\left(\begin{array}{c}{x}^{{}^{\prime }}\\ y^{{}^{\prime }}\end{array}\right)=\left(\begin{array}{cc}co{s}^{\theta }& -si{n}^{\theta }\\ si{n}^{\theta }& co{s}^{\theta }\end{array}\right)\ast \left(\begin{array}{c}x\\ y\end{array}\right)$$

　　附：一般情况下，由于旋转操作会有一定的区域变化，实际操作中会将ROI区域在旋转之前外扩一些以此来降低插值后信息的损失(最终计算还是根据ROI区域大小来进行计算)。

　　3 根据旋转后的半径区域对每个像素点求出梯度幅值与方向，然后再对每个梯度幅值乘以高斯权重系数，以此生成直方图。

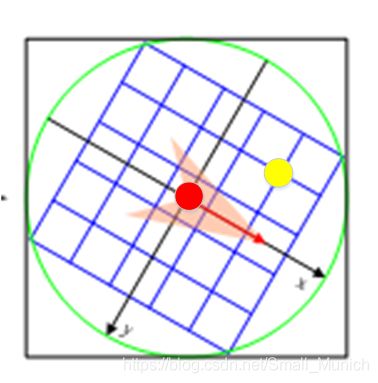
　　3.1 计算梯度幅值：上图中红色圆点为关键点$Center$，黄色圆点为其中一个像素点$Pixel$，那么计算梯度幅值与方向公式为：

$$grad(I_{\sigma }(x,y))=\sqrt{(gradien{t}_{centerx}-gradien{t}_{pixelx}{)}^2+(gradien{t}_{centery}-gradien{t}_{pixely}{)}^2}$$

$$\theta (x,y)=ta{n}^{-1}(\frac{cente{r}_y-pixe{l}_y}{cente{r}_x-pixe{l}_x})$$

上述公式$gradient$为在$x$， $y$方向上的梯度值，$\theta (x,y)$为坐标求取的方向。

　　3.2 求取梯度幅值之后，我们需要对每个梯度幅值乘以高斯权重系数，以此来生成最后存储的方向直方图。

为什么梯度幅值乘以高斯权重系数？

　　原因比较容易理解：距离关键点距离的远近对关键点起作用(可以从局部关联性角度进行理解)不同。

$$weight=|grad(I_{\sigma }(x,y))|\times exp(-\frac{x_w^2+y_w^2}{2{\sigma }_w})\times (1-d_r)\times (1-d_c)\times (1-d_o)$$

参数解释：

　　$x_k$：该点与关键点的列距离；

　　$y_k$：该点与关键点的行距离；

　　${\sigma }_w$：等于描述子窗口宽度$3\sigma \times$直方图列数(取4)的一半；

4 对2x2的每个小子区域内计算8个方向的梯度方向直方图，回执每个梯度方向的累加值，从而形成一个种子点，然后再继续下一个2x2的区域进行梯度方向直方图统计，形成下一个种子点，最后生成16个种子点，排序成为128维一维向量。

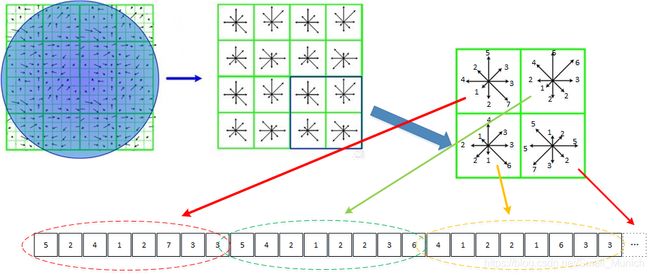
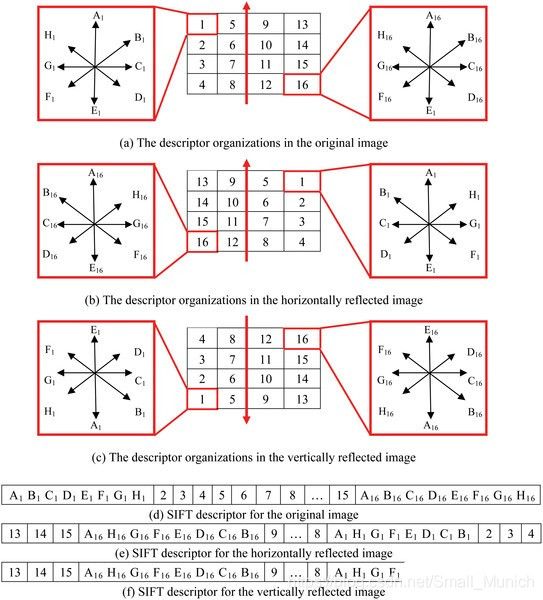
每个小子区域的8个梯度方向直方图值进行存储排序方式有3种：

　　原图正常顺序存储的描述子;

　　水平反射顺序存储的描述子;

　　垂直反射顺序存储的描述子;

示意图如下：

5 形成描述之后，可以进一步对描述子元素门限化及向量规范化：

描述子向量元素门限化：

　　方向直方图每个方向上梯度复制限制在一定的限值一下(门限一般取0.2，此处图像在计算梯度幅值时已经进行归一化)。

描述子向量元素规范化：

$W=(w_1,w_2,\dots ,w_{128})$ 为得到的128维描述子向量

$L=(l_1,l_2,\dots ,l_{128})$ 为规范化后的向量

计算公式：

$$l_j=\frac{w_j}{\sqrt{{\sum }_{i=1}^{128}{w}_i}}$$

　　至此，SIFT算法描述子对于其中一个关键点构建就结束，下面重复对每个关键点构建对应的描述子。

Root-SIFT描述符：

　　Root-SIFT算法出自2012年Three things everyone should know to improve object retrieval. 论文中谈及在进行直方图比较时候，采取欧氏距离性能通常要低于卡方距离和Hellinger核，但是SIFT算法却一直采用欧式距离。我们了解到SIFT描述符本质上也是通过直方图技术，Root-SIFT作者认为使用欧氏距离作为度量源自于SIFT算法提出原因，因此找出一种比欧式距离更加精确的度量准则。

Root-SIFT算法扩展较为简单，仅有如下3步骤：

　　1 提取到SIFT描述子后，对特征向量x进行$l_1$的归一化操作$l_1-normalize$，得到$x^{{}^{\prime }}$。

　　2 对特征向量$x^{{}^{\prime }}$的每一个元素求取平方根。

　　3 进行$l_2-normalize$，可以选择是否采用该步骤。

简单Root-SIFT的Python实现代码：

import numpy as np
import cv2 as cv

class RootSIFT:
	def __init__(self):
		# initialize the SIFT feature extractor
		# self.extractor = cv.DescriptorExtractor_create("SIFT")
		self.extractor = cv.xfeatures2d_SIFT.create()

	def compute(self, image, kps, eps=1e-7):
		# compute SIFT descriptors
		(kps, descs) = self.extractor.compute(image, kps)

		# if there are no keypoints or descriptors, return an empty tuple
		if len(kps) == 0:
			return ([], None)

		# apply the Hellinger kernel by first L1-normalizing and taking the
		# square-root
		descs /= (descs.sum(axis=1, keepdims=True) + eps)
		descs = np.sqrt(descs)
		#descs /= (np.linalg.norm(descs, axis=1, ord=2) + eps)

		# return a tuple of the keypoints and descriptors
		return (kps, descs)

贴一张Root-SIFT论文的实验对比图：

参考文献

https://www.pyimagesearch.com/2015/04/13/implementing-rootsift-in-python-and-opencv/

https://blog.csdn.net/abcjennifer/article/details/7639681

http://www.cs.ubc.ca/~lowe/papers/ijcv04.pdf