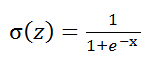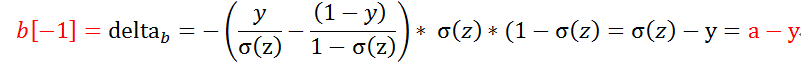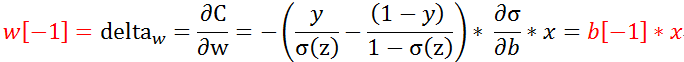机器学习(11.4)--神经网络(nn)算法的深入与优化(4) -- CorssEntropyCost(交叉熵代价函数)数理分析与代码实现
这篇文章我们将从数理上对CorssEntropyCost进行讲解,同时附上实现的代码
首先我们定义
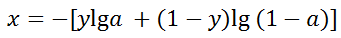
因此在求得最后一层神经元
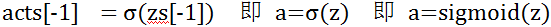
这时我们对最后一层的w,b求偏导数,
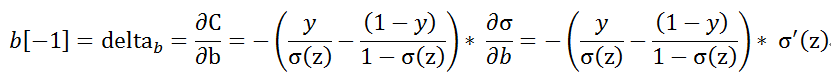
可以参考
机器学习(11.3)--神经网络(nn)算法的深入与优化(3) -- QuadraticCost(二次方代价函数)数理分析
首先我们定义
因此在求得最后一层神经元
这时我们对最后一层的w,b求偏导数,
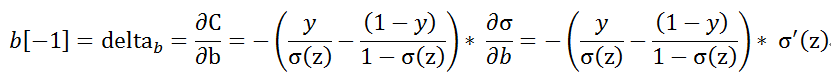
我们在sigmoid函数定义为
其中x在程序代码对应的是a[-2],
def itemData(item,layers,weights,biases):
'''单条记录的正反向计算'''
#正向计算
zs = []
acts = [item[0]]
for w,b in zip(weights,biases):
z = np.dot(w,acts[-1]) + b
zs.append(z)
acts.append(sigmoid(z))
#反向计算
item_w = [np.zeros(b.shape) for b in weights]
item_b = [np.zeros(b.shape) for b in biases]
for index in range(-1,-1 * len(layers),-1):
if index == -1:
item_b[index] = acts[index] - item[1]
else:
item_b[index] = np.dot(weights[index + 1].T,item_b[index + 1])
#二次方代价函数 两个差别只是后面有没有乘 * sigmoid_deriv(zs[index])
#在代码中的差异只是缩进不同,
#item_b[index] = item_b[index] * sigmoid_deriv(zs[index])
item_b[index] = item_b[index] * sigmoid_deriv(zs[index]) #交叉熵代价函数
item_w[index] = np.dot(item_b[index],acts[index - 1].T)
return item_w,item_b虽然在这代码中的CorssEntropyCost(交叉熵代价函数) 与QuadraticCost(二次方代价函数)表现上只是一个缩进,
但原理却是千差万别,在使用QuadraticCost(二次方代价函数)时,使用不同激活函数影响不太大,
但如果使用CorssEntropyCost(交叉熵代价函数),因为中间有一个![]() 的过程
的过程
因此,得到a-y和激活函数是sigmoid是有相关的。
最后附上所有代码
# -*- coding:utf-8 -*-
import pickle
import gzip
import numpy as np
import random
#激活函数
def sigmoid(z):
return 1.0 / (1.0 + np.exp(-z))
def sigmoid_deriv(z):
return sigmoid(z) * (1 - sigmoid(z))
#读取数据
def loadData(trainingNum = None,testNum=None):
with gzip.open(r'mnist.pkl.gz', 'rb') as f:
training_data, validation_data, test_data = pickle.load(f,encoding='bytes')
training_label = np.zeros([training_data[1].shape[0],10,1])
for index,val in enumerate(training_data[1]): training_label[index][val] = 1
training_data = list(zip(training_data[0].reshape(-1,784,1),training_label))
test_data = list(zip(test_data[0].reshape(-1,784,1),test_data[1]))
if trainingNum !=None:
training_data = training_data[0:trainingNum]
if trainingNum !=None:
test_data = test_data[0:testNum]
return training_data,test_data
def batchData(batch,layers,weights,biases):
batch_w = [np.zeros(b.shape) for b in weights]
batch_b = [np.zeros(b.shape) for b in biases]
for item in batch:
item_w,item_b=itemData(item,layers,weights,biases)
#当batch下每条记录计算完后加总
for index in range(0,len(batch_w)):
batch_w[index] = batch_w[index] + item_w[index]
batch_b[index] = batch_b[index] + item_b[index]
return batch_w,batch_b
def itemData(item,layers,weights,biases):
'''单条记录的正反向计算'''
#正向计算
zs = []
acts = [item[0]]
for w,b in zip(weights,biases):
z = np.dot(w,acts[-1]) + b
zs.append(z)
acts.append(sigmoid(z))
#反向计算
item_w = [np.zeros(b.shape) for b in weights]
item_b = [np.zeros(b.shape) for b in biases]
for index in range(-1,-1 * len(layers),-1):
if index == -1:
item_b[index] = acts[index] - item[1]
else:
item_b[index] = np.dot(weights[index + 1].T,item_b[index + 1])
#二次方代价函数 两个差别只是后面有没有乘 * sigmoid_deriv(zs[index])
#在代码中的差异只是进位不同,
#item_b[index] = item_b[index] * sigmoid_deriv(zs[index])
item_b[index] = item_b[index] * sigmoid_deriv(zs[index]) #交叉熵代价函数
item_w[index] = np.dot(item_b[index],acts[index - 1].T)
return item_w,item_b
def predict(test_data,weights,biases):
#6、正向计算测试集:计算出结果
#7、和正确结果比较,统计出正确率
correctNum=0
for testImg,testLabel in test_data:
for w,b in zip( weights,biases):
testImg= sigmoid(np.dot(w, testImg)+b)
if np.argmax(testImg)==testLabel : correctNum+=1
return correctNum
def mnistNN(trainingNum = None,testNum = None,midLayes=[20,15],epochs=6,batchNum=10,learningRate=3):
training_data,test_data=loadData(trainingNum,testNum)
#1、读取数据,调整数据格式以适配算法,设置基本参数
layers = [training_data[0][0].shape[0]]+midLayes+[training_data[0][1].shape[0]]
trainingNum = len(training_data)
#2、建立初始化的weights和biases
weights = [np.random.randn(layers[x + 1],layers[x]) for x in range(len(layers) - 1)]
biases = [np.random.randn(layers[x + 1],1) for x in range(len(layers) - 1)]
for j in range(epochs):
random.shuffle(training_data)
batchGroup = [training_data[x:x + batchNum] for x in range(0,trainingNum,batchNum)]
for batch in batchGroup:
batch_w,batch_b=batchData(batch,layers,weights,biases)
#一组batch计算结束后,求平均并修正weights和biases
for index in range(0,len(batch_w)):
batch_w[index] = batch_w[index] / batchNum
weights[index] = weights[index] - learningRate * batch_w[index]
batch_b[index] = batch_b[index] / batchNum
biases[index] = biases[index] - learningRate * batch_b[index]
print("共 %d 轮训练,第 %d 轮训练结束,测试集数量为 %d 条,测试正确 %d 条。"%(epochs,j+1,len(test_data),predict(test_data,weights,biases)))
#参数组1 多调试几次,你会发现这组数据结果比较不稳定
mnistNN(midLayes=[30],epochs=15,learningRate=3)