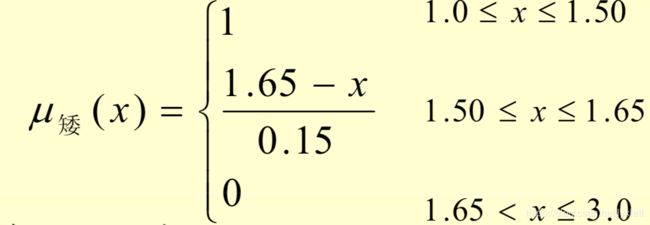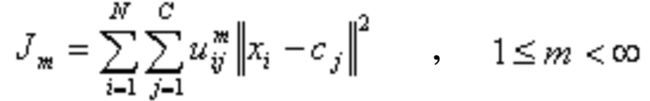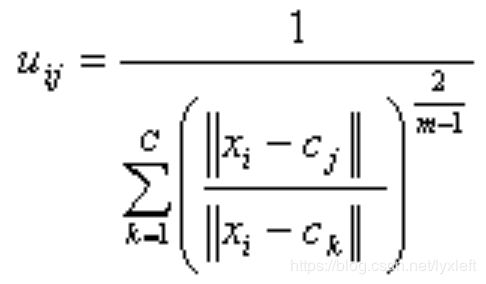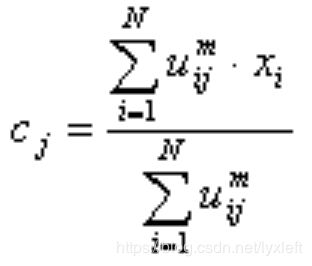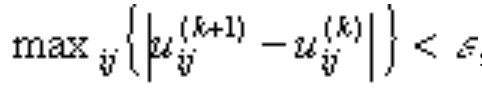Fuzzy C-Means（模糊C均值聚类）算法原理详解与python实现
目录
模糊理论
Fuzzy C-Means算法原理
算法步骤
python实现
参考资料
本文采用数据集为iris,将iris.txt放在程序的同一文件夹下。请先自行下载好。
模糊理论
模糊控制是自动化控制领域的一项经典方法。其原理则是模糊数学、模糊逻辑。1965，L. A. Zadeh发表模糊集合“Fuzzy Sets”的论文， 首次引入隶属度函数的概念，打破了经典数学“非0即 1”的局限性，用[0,1]之间的实数来描述中间状态。
很多经典的集合（即：论域U内的某个元素是否属于集合A，可以用一个数值来表示。在经典集合中，要么0，要么1）不能描述很多事物的属性，需要用模糊性词语来判断。比如天气冷热程度、人的胖瘦程度等等。模糊数学和模糊逻辑把只取1或0二值（属于/不属于）的普通集合概念推广0~1区间内的多个取值，即隶属度。用“隶属度”来描述元素和集合之间的关系。
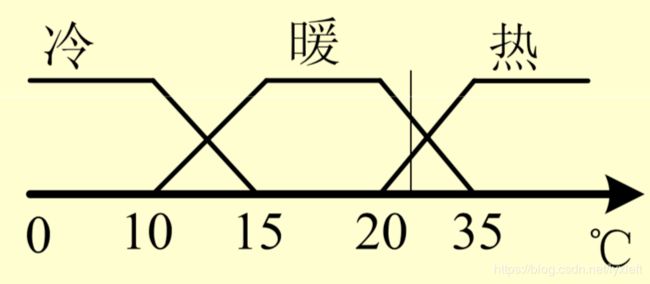
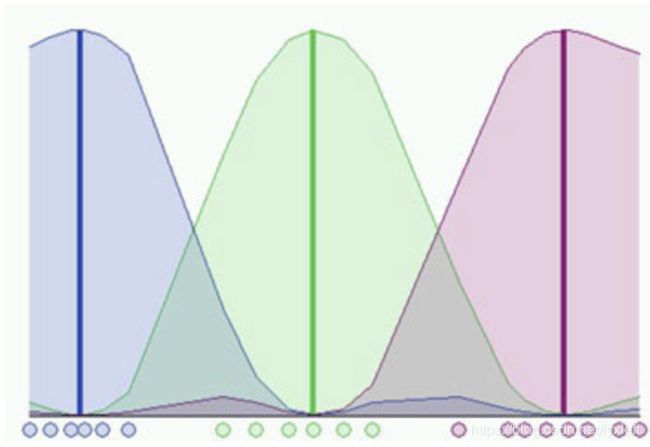
如图所示，对于冷热程度，我们采取三个模糊子集：冷、暖、热。对于某一个温度，可能同时属于两个子集。要进一步具体判断，我们就需要提供一个描述“程度”的函数，即隶属度。
例如，身高可以分为“高”、“中等”、“矮”三个子集。取论域U（即人的身高范围）为[1.0,3.0]，单位m。在U上定义三个隶属度函数来确定身高与三个模糊子集的关系：
模糊规则的设定：
(1)专家的经验和知识
– 藉由询问经验丰富的专家，在获得系统的知 识后，将知识改为IF....THEN ....的型式。
(2)操作员的操作模式
– 记录熟练的操作员的操作模式，并将其整理为IF....THEN ....的型式。
(3)自学习
– 设定的模糊规则可能存在偏差，模糊控制器能依设定的目标，增加或修改模糊控制规则
Fuzzy C-Means算法原理
模糊c均值聚类融合了模糊理论的精髓。相较于k-means的硬聚类，模糊c提供了更加灵活的聚类结果。因为大部分情况下，数据集中的对象不能划分成为明显分离的簇，指派一个对象到一个特定的簇有些生硬，也可能会出错。故，对每个对象和每个簇赋予一个权值，指明对象属于该簇的程度。当然，基于概率的方法也可以给出这样的权值，但是有时候我们很难确定一个合适的统计模型，因此使用具有自然地、非概率特性的模糊c均值就是一个比较好的选择。
简单地说，就是要最小化目标函数Jm:（在一些资料中也定义为SSE即误差的平方和）
其中m是聚类的簇数；i，j是类标号；
表示样本
属于j类的隶属度。i表示第i个样本，x是具有d维特征的一个样本。
是j簇的中心，也具有d维度。||*||可以是任意表示距离的度量。关于有哪些基于距离的度量，可参考我的另一篇博文《数据的相似性和相异性的度量》。
模糊c是一个不断迭代计算隶属度和簇中心的过程，直到他们达到最优。
，
注：对于单个样本，它对于每个簇的隶属度之和为1。
迭代的终止条件为：
其中k是迭代步数，
是误差阈值。上式含义是，继续迭代下去，隶属程度也不会发生较大的变化。即认为隶属度不变了，已经达到比较优（局部最优或全局最优）状态了。该过程收敛于目标Jm的局部最小值或鞍点。
抛开复杂的算式，这个算法的意思就是：给每个样本赋予属于每个簇的隶属度函数。通过隶属度值大小来将样本归类。
算法步骤
1、初始化
通常采用随机初始化。即权值随机地选取。簇数需要人为选定。
2、计算质心
FCM中的质心有别于传统质心的地方在于，它是以隶属度为权重做一个加权平均。
3、更新模糊伪划分
即更新权重（隶属度）。简单地说，如果x越靠近质心c，则隶属度越高，反之越低。
python实现
这段代码是以iris数据集为例的，雏形源于网络，在错误的地方做了一些修正。是专门针对iris写的：
如果要使用你自己的数据集，请看第二段代码。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Wed Mar 27 10:51:45 2019
@author: youxinlin
"""
import copy
import math
import random
import time
global MAX # 用于初始化隶属度矩阵U
MAX = 10000.0
global Epsilon # 结束条件
Epsilon = 0.0000001
def import_data_format_iris(file):
"""
file这里是输入文件的路径，如iris.txt.
格式化数据，前四列为data，最后一列为类标号（有0，1，2三类）
如果是你自己的data，就不需要执行此段函数了。
"""
data = []
cluster_location =[]
with open(str(file), 'r') as f:
for line in f:
current = line.strip().split(",") #对每一行以逗号为分割，返回一个list
current_dummy = []
for j in range(0, len(current)-1):
current_dummy.append(float(current[j])) #current_dummy存放data
#下面注这段话提供了一个范例：若类标号不是0，1，2之类数字时该怎么给数据集
j += 1
if current[j] == "Iris-setosa\n":
cluster_location.append(0)
elif current[j] == "Iris-versicolor\n":
cluster_location.append(1)
else:
cluster_location.append(2)
data.append(current_dummy)
print("加载数据完毕")
return data
# return data , cluster_location
def randomize_data(data):
"""
该功能将数据随机化，并保持随机化顺序的记录
"""
order = list(range(0, len(data)))
random.shuffle(order)
new_data = [[] for i in range(0, len(data))]
for index in range(0, len(order)):
new_data[index] = data[order[index]]
return new_data, order
def de_randomise_data(data, order):
"""
此函数将返回数据的原始顺序，将randomise_data()返回的order列表作为参数
"""
new_data = [[]for i in range(0, len(data))]
for index in range(len(order)):
new_data[order[index]] = data[index]
return new_data
def print_matrix(list):
"""
以可重复的方式打印矩阵
"""
for i in range(0, len(list)):
print (list[i])
def initialize_U(data, cluster_number):
"""
这个函数是隶属度矩阵U的每行加起来都为1. 此处需要一个全局变量MAX.
"""
global MAX
U = []
for i in range(0, len(data)):
current = []
rand_sum = 0.0
for j in range(0, cluster_number):
dummy = random.randint(1,int(MAX))
current.append(dummy)
rand_sum += dummy
for j in range(0, cluster_number):
current[j] = current[j] / rand_sum
U.append(current)
return U
def distance(point, center):
"""
该函数计算2点之间的距离（作为列表）。我们指欧几里德距离。闵可夫斯基距离
"""
if len(point) != len(center):
return -1
dummy = 0.0
for i in range(0, len(point)):
dummy += abs(point[i] - center[i]) ** 2
return math.sqrt(dummy)
def end_conditon(U, U_old):
"""
结束条件。当U矩阵随着连续迭代停止变化时，触发结束
"""
global Epsilon
for i in range(0, len(U)):
for j in range(0, len(U[0])):
if abs(U[i][j] - U_old[i][j]) > Epsilon :
return False
return True
def normalise_U(U):
"""
在聚类结束时使U模糊化。每个样本的隶属度最大的为1，其余为0
"""
for i in range(0, len(U)):
maximum = max(U[i])
for j in range(0, len(U[0])):
if U[i][j] != maximum:
U[i][j] = 0
else:
U[i][j] = 1
return U
# m的最佳取值范围为[1.5，2.5]
def fuzzy(data, cluster_number, m):
"""
这是主函数，它将计算所需的聚类中心，并返回最终的归一化隶属矩阵U.
参数是：簇数(cluster_number)和隶属度的因子(m)
"""
# 初始化隶属度矩阵U
U = initialize_U(data, cluster_number)
# print_matrix(U)
# 循环更新U
while (True):
# 创建它的副本，以检查结束条件
U_old = copy.deepcopy(U)
# 计算聚类中心
C = []
for j in range(0, cluster_number):
current_cluster_center = []
for i in range(0, len(data[0])):
dummy_sum_num = 0.0
dummy_sum_dum = 0.0
for k in range(0, len(data)):
# 分子
dummy_sum_num += (U[k][j] ** m) * data[k][i]
# 分母
dummy_sum_dum += (U[k][j] ** m)
# 第i列的聚类中心
current_cluster_center.append(dummy_sum_num/dummy_sum_dum)
# 第j簇的所有聚类中心
C.append(current_cluster_center)
# 创建一个距离向量, 用于计算U矩阵。
distance_matrix =[]
for i in range(0, len(data)):
current = []
for j in range(0, cluster_number):
current.append(distance(data[i], C[j]))
distance_matrix.append(current)
# 更新U
for j in range(0, cluster_number):
for i in range(0, len(data)):
dummy = 0.0
for k in range(0, cluster_number):
# 分母
dummy += (distance_matrix[i][j ] / distance_matrix[i][k]) ** (2/(m-1))
U[i][j] = 1 / dummy
if end_conditon(U, U_old):
print ("结束聚类")
break
print ("标准化 U")
U = normalise_U(U)
return U
def checker_iris(final_location):
"""
和真实的聚类结果进行校验比对
"""
right = 0.0
for k in range(0, 3):
checker =[0,0,0]
for i in range(0, 50):
for j in range(0, len(final_location[0])):
if final_location[i + (50*k)][j] == 1: #i+(50*k)表示 j表示第j类
checker[j] += 1 #checker分别统计每一类分类正确的个数
right += max(checker) #累加分类正确的个数
print ('分类正确的个数是:',right)
answer = right / 150 * 100
return "准确率：" + str(answer) + "%"
if __name__ == '__main__':
# 加载数据
data = import_data_format_iris("iris.txt")
# print_matrix(data)
# 随机化数据
data , order = randomize_data(data)
# print_matrix(data)
start = time.time()
# 现在我们有一个名为data的列表，它只是数字
# 我们还有另一个名为cluster_location的列表，它给出了正确的聚类结果位置
# 调用模糊C均值函数
final_location = fuzzy(data , 3 , 2)
# 还原数据
final_location = de_randomise_data(final_location, order)
# print_matrix(final_location)
# 准确度分析
print (checker_iris(final_location))
print ("用时：{0}".format(time.time() - start))如果要用你自己的数据集做聚类：替换下面代码的data为你自己的数据集；自己写一个准确率的判断方法。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Wed Mar 27 10:51:45 2019
模糊c聚类:https://blog.csdn.net/lyxleft/article/details/88964494
@author: youxinlin
"""
import copy
import math
import random
import time
global MAX # 用于初始化隶属度矩阵U
MAX = 10000.0
global Epsilon # 结束条件
Epsilon = 0.0000001
def print_matrix(list):
"""
以可重复的方式打印矩阵
"""
for i in range(0, len(list)):
print (list[i])
def initialize_U(data, cluster_number):
"""
这个函数是隶属度矩阵U的每行加起来都为1. 此处需要一个全局变量MAX.
"""
global MAX
U = []
for i in range(0, len(data)):
current = []
rand_sum = 0.0
for j in range(0, cluster_number):
dummy = random.randint(1,int(MAX))
current.append(dummy)
rand_sum += dummy
for j in range(0, cluster_number):
current[j] = current[j] / rand_sum
U.append(current)
return U
def distance(point, center):
"""
该函数计算2点之间的距离（作为列表）。我们指欧几里德距离。闵可夫斯基距离
"""
if len(point) != len(center):
return -1
dummy = 0.0
for i in range(0, len(point)):
dummy += abs(point[i] - center[i]) ** 2
return math.sqrt(dummy)
def end_conditon(U, U_old):
"""
结束条件。当U矩阵随着连续迭代停止变化时，触发结束
"""
global Epsilon
for i in range(0, len(U)):
for j in range(0, len(U[0])):
if abs(U[i][j] - U_old[i][j]) > Epsilon :
return False
return True
def normalise_U(U):
"""
在聚类结束时使U模糊化。每个样本的隶属度最大的为1，其余为0
"""
for i in range(0, len(U)):
maximum = max(U[i])
for j in range(0, len(U[0])):
if U[i][j] != maximum:
U[i][j] = 0
else:
U[i][j] = 1
return U
def fuzzy(data, cluster_number, m):
"""
这是主函数，它将计算所需的聚类中心，并返回最终的归一化隶属矩阵U.
输入参数：簇数(cluster_number)、隶属度的因子(m)的最佳取值范围为[1.5，2.5]
"""
# 初始化隶属度矩阵U
U = initialize_U(data, cluster_number)
# print_matrix(U)
# 循环更新U
while (True):
# 创建它的副本，以检查结束条件
U_old = copy.deepcopy(U)
# 计算聚类中心
C = []
for j in range(0, cluster_number):
current_cluster_center = []
for i in range(0, len(data[0])):
dummy_sum_num = 0.0
dummy_sum_dum = 0.0
for k in range(0, len(data)):
# 分子
dummy_sum_num += (U[k][j] ** m) * data[k][i]
# 分母
dummy_sum_dum += (U[k][j] ** m)
# 第i列的聚类中心
current_cluster_center.append(dummy_sum_num/dummy_sum_dum)
# 第j簇的所有聚类中心
C.append(current_cluster_center)
# 创建一个距离向量, 用于计算U矩阵。
distance_matrix =[]
for i in range(0, len(data)):
current = []
for j in range(0, cluster_number):
current.append(distance(data[i], C[j]))
distance_matrix.append(current)
# 更新U
for j in range(0, cluster_number):
for i in range(0, len(data)):
dummy = 0.0
for k in range(0, cluster_number):
# 分母
dummy += (distance_matrix[i][j ] / distance_matrix[i][k]) ** (2/(m-1))
U[i][j] = 1 / dummy
if end_conditon(U, U_old):
print ("已完成聚类")
break
U = normalise_U(U)
return U
if __name__ == '__main__':
data= [[6.1, 2.8, 4.7, 1.2], [5.1, 3.4, 1.5, 0.2], [6.0, 3.4, 4.5, 1.6], [4.6, 3.1, 1.5, 0.2], [6.7, 3.3, 5.7, 2.1], [7.2, 3.0, 5.8, 1.6], [6.7, 3.1, 4.4, 1.4], [6.4, 2.7, 5.3, 1.9], [4.8, 3.0, 1.4, 0.3], [7.9, 3.8, 6.4, 2.0], [5.2, 3.5, 1.5, 0.2], [5.9, 3.0, 5.1, 1.8], [5.7, 2.8, 4.1, 1.3], [6.8, 3.2, 5.9, 2.3], [5.4, 3.4, 1.5, 0.4], [5.4, 3.7, 1.5, 0.2], [6.6, 3.0, 4.4, 1.4], [5.1, 3.5, 1.4, 0.2], [6.0, 2.2, 4.0, 1.0], [7.7, 2.8, 6.7, 2.0], [6.3, 2.8, 5.1, 1.5], [7.4, 2.8, 6.1, 1.9], [5.5, 4.2, 1.4, 0.2], [5.7, 3.0, 4.2, 1.2], [5.5, 2.6, 4.4, 1.2], [5.2, 3.4, 1.4, 0.2], [4.9, 3.1, 1.5, 0.1], [4.6, 3.6, 1.0, 0.2], [4.6, 3.2, 1.4, 0.2], [5.8, 2.7, 3.9, 1.2], [5.0, 3.4, 1.5, 0.2], [6.1, 3.0, 4.6, 1.4], [4.7, 3.2, 1.6, 0.2], [6.7, 3.3, 5.7, 2.5], [6.5, 3.0, 5.8, 2.2], [5.4, 3.4, 1.7, 0.2], [5.8, 2.7, 5.1, 1.9], [5.4, 3.9, 1.3, 0.4], [5.3, 3.7, 1.5, 0.2], [6.1, 3.0, 4.9, 1.8], [7.2, 3.2, 6.0, 1.8], [5.5, 2.3, 4.0, 1.3], [5.7, 2.8, 4.5, 1.3], [4.9, 2.4, 3.3, 1.0], [5.4, 3.0, 4.5, 1.5], [5.0, 3.5, 1.6, 0.6], [5.2, 4.1, 1.5, 0.1], [5.8, 4.0, 1.2, 0.2], [5.4, 3.9, 1.7, 0.4], [6.5, 3.2, 5.1, 2.0], [5.5, 2.4, 3.7, 1.0], [5.0, 3.5, 1.3, 0.3], [6.3, 2.5, 5.0, 1.9], [6.9, 3.1, 4.9, 1.5], [6.2, 2.2, 4.5, 1.5], [6.3, 3.3, 4.7, 1.6], [6.4, 3.2, 4.5, 1.5], [4.7, 3.2, 1.3, 0.2], [5.5, 2.4, 3.8, 1.1], [5.0, 2.0, 3.5, 1.0], [4.4, 2.9, 1.4, 0.2], [4.8, 3.4, 1.9, 0.2], [6.3, 3.4, 5.6, 2.4], [5.5, 2.5, 4.0, 1.3], [5.7, 2.5, 5.0, 2.0], [6.5, 3.0, 5.2, 2.0], [6.7, 3.0, 5.0, 1.7], [5.2, 2.7, 3.9, 1.4], [6.9, 3.1, 5.1, 2.3], [7.2, 3.6, 6.1, 2.5], [4.8, 3.0, 1.4, 0.1], [6.3, 2.9, 5.6, 1.8], [5.1, 3.5, 1.4, 0.3], [6.9, 3.1, 5.4, 2.1], [5.6, 3.0, 4.1, 1.3], [7.7, 2.6, 6.9, 2.3], [6.4, 2.9, 4.3, 1.3], [5.8, 2.7, 4.1, 1.0], [6.1, 2.9, 4.7, 1.4], [5.7, 2.9, 4.2, 1.3], [6.2, 2.8, 4.8, 1.8], [4.8, 3.4, 1.6, 0.2], [5.6, 2.9, 3.6, 1.3], [6.7, 2.5, 5.8, 1.8], [5.0, 3.4, 1.6, 0.4], [6.3, 3.3, 6.0, 2.5], [5.1, 3.8, 1.9, 0.4], [6.6, 2.9, 4.6, 1.3], [5.1, 3.3, 1.7, 0.5], [6.3, 2.5, 4.9, 1.5], [6.4, 3.1, 5.5, 1.8], [6.2, 3.4, 5.4, 2.3], [6.7, 3.1, 5.6, 2.4], [4.6, 3.4, 1.4, 0.3], [5.5, 3.5, 1.3, 0.2], [5.6, 2.7, 4.2, 1.3], [5.6, 2.8, 4.9, 2.0], [6.2, 2.9, 4.3, 1.3], [7.0, 3.2, 4.7, 1.4], [5.0, 3.2, 1.2, 0.2], [4.3, 3.0, 1.1, 0.1], [7.7, 3.8, 6.7, 2.2], [5.6, 3.0, 4.5, 1.5], [5.8, 2.7, 5.1, 1.9], [5.8, 2.8, 5.1, 2.4], [4.9, 3.1, 1.5, 0.1], [5.7, 3.8, 1.7, 0.3], [7.1, 3.0, 5.9, 2.1], [5.1, 3.7, 1.5, 0.4], [6.3, 2.7, 4.9, 1.8], [6.7, 3.0, 5.2, 2.3], [5.1, 2.5, 3.0, 1.1], [7.6, 3.0, 6.6, 2.1], [4.5, 2.3, 1.3, 0.3], [4.9, 3.0, 1.4, 0.2], [6.5, 2.8, 4.6, 1.5], [5.7, 4.4, 1.5, 0.4], [6.8, 3.0, 5.5, 2.1], [4.9, 2.5, 4.5, 1.7], [5.1, 3.8, 1.5, 0.3], [6.5, 3.0, 5.5, 1.8], [5.7, 2.6, 3.5, 1.0], [5.1, 3.8, 1.6, 0.2], [5.9, 3.0, 4.2, 1.5], [6.4, 3.2, 5.3, 2.3], [4.4, 3.0, 1.3, 0.2], [6.1, 2.8, 4.0, 1.3], [6.3, 2.3, 4.4, 1.3], [5.0, 2.3, 3.3, 1.0], [5.0, 3.6, 1.4, 0.2], [5.9, 3.2, 4.8, 1.8], [6.4, 2.8, 5.6, 2.2], [6.1, 2.6, 5.6, 1.4], [5.6, 2.5, 3.9, 1.1], [6.0, 2.7, 5.1, 1.6], [6.0, 3.0, 4.8, 1.8], [6.4, 2.8, 5.6, 2.1], [6.0, 2.9, 4.5, 1.5], [5.8, 2.6, 4.0, 1.2], [7.7, 3.0, 6.1, 2.3], [5.0, 3.3, 1.4, 0.2], [6.9, 3.2, 5.7, 2.3], [6.8, 2.8, 4.8, 1.4], [4.8, 3.1, 1.6, 0.2], [6.7, 3.1, 4.7, 1.5], [4.9, 3.1, 1.5, 0.1], [7.3, 2.9, 6.3, 1.8], [4.4, 3.2, 1.3, 0.2], [6.0, 2.2, 5.0, 1.5], [5.0, 3.0, 1.6, 0.2]]
start = time.time()
# 调用模糊C均值函数
res_U = fuzzy(data , 3 , 2)
# 计算准确率
print ("用时：{0}".format(time.time() - start))参考资料
J. C. Dunn (1973): "A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters", Journal of Cybernetics 3: 32-57
J. C. Bezdek (1981): "Pattern Recognition with Fuzzy Objective Function Algoritms", Plenum Press, New York
Pang-Ning Tan, et al.数据挖掘导论
http://home.deib.polimi.it/matteucc/Clustering/tutorial_html/cmeans.html
https://blog.csdn.net/zwqhehe/article/details/75174918
