RePr Improved Training of Convolutional Filters阅读翻译
论文地址:https://arxiv.org/abs/1811.07275 CVPR2019的Oral Paper
代码:作者目前没公布,Reddit上对于这篇论文的讨论很激烈┓( ´∀` )┏,对于代码复现很多人都有问题(比如:复现1),加上作者目前还没开源代码。所以想看戏的可以去→_→传送门(可能需要梯子)
作者:Aaditya Prakash, James Storer, Dinei Florencio, Cha Zhang
参考资料:[CVPR2019]:专门为卷积神经网络设计的训练方法:RePr-知乎
目录
- 摘要
- 1.介绍
- 2.相关工作
- 3.正交特征(Orthogonal Features)的动机
- 4.我们的训练Scheme:RePr
- 5.我们的度量:filter间的正交( inter-filter orthogonality)
- 6.Ablation研究
- 7.正交与蒸馏(Orthogonality and Distillation)
- 8.结果
- 9.结论
- 附录
- ImageNet训练细节
- 超参数
摘要
训练良好的卷积神经网络可以很容易被裁剪(pruning)而不显著降低性能。这是因为网络filters在提取特征时存在不必要的重叠。网络架构的创新,例如skip / dense连接和Inception单元在某种程度上缓解了这个问题,但这些改进伴随着运行时计算和内存需求的增加。我们试图从另一个角度解决这个问题——不是通过改变网络结构,而是通过改变训练方法。我们通过临时裁剪部分filters,之后再恢复这部分模型filters,并循环重复此过程来表明,这种方法减少了学习特征过程中的重叠,模型泛化能力进一步提高。我们在本文中表明,现有的模型剪枝标准在剪枝选择filters的过程中不是最优的,并引入filters间的正交性作为排序标准来确定表达不足的filters。我们的方法既适用于vanilla卷积网络,也适用于更复杂的现代架构,可以提高各种任务的性能,尤其是应用于小型网络时。
1.介绍
卷积神经网络在各种计算机视觉任务中取得了最先进的成果[1,2]。这种成功很大程度上归功于一种新颖的,任务特定的网络架构的创新[3,4]。尽管网络设计存在差异,但不同任务使用的是相同的优化技术。这些技术将每个权重视为单独的实体并独立更新。在开发专门为卷积网络设计的训练过程方面取得了有限的进展,其中filters是网络的基本单元。一个filter不是单个权重参数,而是a stack of spatial kernels。
由于模型通常过度参数化,训练过的卷积网络将包含冗余的filters[5,6]。这就是实现模型压缩的常见做法是裁剪filters[7,8,9,10,11]而不是单独参数[12]的证据。大多数这些修剪方法能够丢弃大量filters,而模型的性能只有轻微的损失。然而具有较少filters的模型不能从头开始训练达到和已被修剪为大致相同尺寸的大型模型的性能[6,11,13]。标准训练应该过程倾向于学习具有不相关与可修剪的filters的模型,即使对于没有任何多余容量的架构也是如此。这表明卷积神经网络(convnets)的训练有改进的余地。
为此,我们提出了一种训练方案,其中在经过一定数量的标准训练迭代后,我们选择暂时丢弃一部分模型filters。在对简化网络进行额外训练后,我们重新引入先前丢弃的filters,使用新权重进行初始化,并继续进行标准训练。我们观察到,在重新引入之前丢弃的filters之后,该模型能够比下降之前获得更高的性能。重复应用该过程获得的模型优于通过标准训练获得的模型,如图1所示并在第4节中讨论。我们在各种任务和各种类型的卷积网络中都观察到了这种改进。该训练过程能够在一系列可能的标准中选择要丢弃的filters从而产生改进的性能,并且通过仔细选择排序标准可以实现进一步的增益。根据最近的一个假设[14],过度参数化网络的相对成功可能主要归因于大量初始子网络。我们的方法旨在保留成功的子网络,同时允许重新初始化不太有用的filters。

除了我们新颖的训练策略之外,我们工作第二个主要贡献是探索filters丢弃的标准。我们的实验表明,标准的永久filter裁剪技术在我们的设置中并不是最优的,我们提出了一个可以有效计算的替代度量,并且可以显著提高性能。我们基于卷积层内filters间的正交性(inter-filter orthogonality)提出了一个度量,并表明在我们的训练策略环境中该度量方法优于目前网络裁剪中最先进的基于filter重要性排序的方法。我们观察到即使是小型,参数不足的(under-parameterized)网络也倾向于学习冗余filters,这表明filters冗余不仅仅是过度参数化(over-parameterization)的结果,还和无效的训练有关。我们的目标是减少filters冗余并提高卷积网络的表达能力,我们通过改变训练计划(Training Scheme)而不是模型架构来实现这一目标。
2.相关工作
训练计划(Training Scheme) 目前已经提出了许多针对训练方法的改变,用于减少过拟合并提高泛化能力。Dropout[15]广泛应用于训练深层网络。通过随机丢弃神经元,它可以防止特征检测器的共同适应(co-adaption)。通过丢弃每层部分激活函数可以实现类似的效果[16]。Wu等人 [15]通过卷积激活值的概率pooling将随机dropping的概念扩展到卷积神经网络。另一种形式的随机训练建议随机丢弃整个层[17],迫使模型学习各层之间的相似特征,以防止极度过拟合。相比之下,我们的技术鼓励模型使用线性特征组合,而不是复制相同的特征。Han等人[18]提出了一种类似的训练方案Dense-Sparse-Dense(DSD),它在训练中应用权重正则化鼓励稀疏权重的发展,并随后去除正则化以恢复密集权重。然而DSD是在独立的参数上工作,而我们的方法专门设计用于卷积filters。
模型压缩(Model Compression) 知识提取(或称为知识蒸馏)(Knowledge Distillation ,KD)[19]是一种训练方法,它使用来自较大的已训练模型(teacher)的soft logits来训练较小的模型(student)。Soft logit捕获对象的层级信息,并为优化提供更平滑的损失函数。这使得小型模型的训练更容易,收敛更好。令人惊讶的结果,Born-Again-Network [20]表明如果student模型与teacher具有相同的容量,它可以胜过teacher。目前已经提出了一些KD的变体[21]并且所有这些变体都需要训练几个模型。我们的训练方案不依赖于外部teacher,并且需要的训练少于KD。更重要的是,当与KD结合使用时,我们的方法比单独使用任何一种技术都能提供更好的性能(在第7节中讨论)。
感谢@pengkingli提供的知识, Soft logits由hinton提出,应用于知识蒸馏领域。具体含义与细节见:Hinton 新作「在线蒸馏」,提升深度学习分布式训练表现的利器
神经元排序(Neuron ranking)寻找最不显著的神经元/权重具有悠久的历史。LeCun [22]和Hassibi等[23]表明,使用含有二阶导数的Hessian可以识别弱神经元,并且比使用权重的大小去识别表现更好。计算Hessian很昂贵,因此没有被广泛使用。Han等人[12] 表明权重的范数仍然是有效的排名标准,并产生稀疏模型(sparse models)。稀疏模型不能转化为更快的推理,但作为神经元排序标准,它们是有效的。Hu等人[24] 探索激活函数中零点的平均百分比(Average Percentage of Zeros ,APoZ),并使用数据驱动的阈值来确定截止点。Molchanov等人[9] 推荐损失函数的泰勒展开的第二项。我们提供详细的比较,并在第5节中展示基于我们的训练计划使用这些指标的结果。
架构搜索(Architecture Search)神经架构搜索[25,26,27]是在训练期间修改网络结构,并且在给定的数据集上探索多个神经网络结构以搜索的最佳网络结构。如果提前固定架构,这些方法将没有任何用。我们的scheme是通过更好地利用可用参数来改进给定的网络架构的训练。如果最终网络结构具有一定的灵活性,或者由于模型已部署,内存要求以及其他因素而固定网络结构时,可以将我们的scheme与架构搜索结合使用。
特征相关(Feature correlation)普通卷积网络的一个众所周知的缺点是它们的相关特征图(correlated feature maps)[5,28]。像Inception-Net [29]这样的架构是通过分析跨层特征的相关性统计启发得来的。随后的研究表明[30],他们是通过级联(concatenated )来自不同大小的filters特征减少层之间的相关性。最新的体系结构如ResNet [1]和DenseNet [31]通过对先前层的激活进行求和或连接来隐式(implicitly)减少特征相关性。也就是说,这些模型的计算成本很高,并且需要大量内存来存储以前的激活。我们的目标是在不改变卷积网络架构的情况下诱导(induce)不相关的特征。这对现有的所有ConvNet实现都有利,并且无需更改基础架构。虽然我们的技术在普通 ConvNet架构中表现最佳,但它仍然略微提高了现代架构的性能。
3.正交特征(Orthogonal Features)的动机
卷积滤波器的特征被定义为来自滤波器的各个核的激活的逐点和。如果某个特征有助于改进模型的泛化能力,则该特征被认为是有用的。泛化能力较差的模型通常具有总体上捕获激活空间中有限方向的特征[32]。换句话说,如果模型的特征彼此正交,它们将各自捕获激活空间中的不同方向,从而导致模型泛化能力的提升。对于一个简单的(trivially sized)ConvNet,我们可以通过分析各层特征的相关性并将它们聚类成组来计算最大表现力的filters[33]。然而,对于在实际应用中使用的深层ConvNets,该方案在计算上是不切实际的。或者,计算上可行的选项是在标准SGD训练中给损失函数加入正则化项,这有助于最小化激活的协方差,但这仅对模型性能产生有限的改进[34,5]。一种类似的方法,其中正则化项反而鼓励filters权重的正交性,也产生了微小的改进[35,36,37,38]。Shang等人[39] 发现低级filters是以相反的phase重复的。强制filters正交将最小化此重复,并且不会更改激活函数。除了性能和泛化能力方面的改进外,Saxe等人 [40]表明权重的正交能提高训练期间网络收敛的稳定性。[38,41]的作者进一步证明了正交权重对网络有效训练的价值。正交初始化是RNN的常见做法,因为它们对初始条件的十分敏感[42],但它有点不受ConvNets的青睐。这些因素决定了我们采取ConvNet中特征正交性的动机,并构成了我们排名标准的基础。因为特征取决于输入数据,所以确定它们的正交性需要在整个训练集中计算统计数据,这样做十分困难。所以我们计算filter权重的正交性来作为替代。我们的实验表明,通过正则化项来促进权重正交不足以推动特征的发展, which capture the full space of the input data manifold。我们把丢弃重叠filters的方法充当隐式正则化,并且在不妨碍模型收敛的情况下导致filters更好的正交性。
我们使用标准相关性分析(Canonical Correlation Analysis,CCA)[43]来研究单层特征的重叠。CCA能反映随机变量的线性组合,显示出它们之间的最大相关性。它是一种有用的工具,用于确定所学习的特征是否在其代表性能力中重叠。Li等人[44] 将相关性分析应用于filter激活,显示出大多数著名的ConvNet架构学习相似的表示。Raghu等人[30] 将CCA与SVD结合起来,对来自不同层的激活的奇异值进行相关分析。他们表明,增加模型的深度并不总是导致模型维度的相应增加,这是由于多个层是在相关联的方向上学习表达。我们问一个更基本的问题 - 单层内各种filters的激活有多相关?在像VGG-16这样的过度参数化网络中,它有几个卷积层每层有512个filters,因此大多数filters激活都是高度相关的。因此,VGG-16已经被证明易于修剪 - 超过50%的filters可以被丢弃,同时保持整个网络的性能[9,44]。这对于在数据集上欠拟合的小得多的卷积网络也是如此吗?
我们将考虑一个简单的两层卷积网络,每层32个filters,最后连接一个softmax层。使用退火学习率在CIFAR-10上训练该模型100个epochs,测试集准确度为58.2%,远低于VGG-16实现的93.5%。在VGG-16的情况下,我们可能期望filters之间的相关性仅仅是模型过度参数化的假象 - 数据集的维度不够高,不足以要求每个特征彼此正交。另一方面,我们的小型网络显然未能捕获训练数据的完整特征空间,因此filters之间的任何相关性都是由于训练效率低下而非过度参数化导致的。
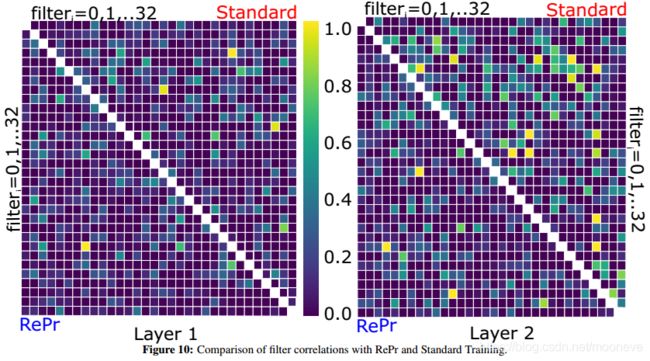
给定训练模型,我们可以通过移除(归零)该filter并测量测试集上的精度下降来评估每个滤波器对模型性能的贡献。我们将这种filter重要性度量称为“greedy Oracle”。我们对模型中的每个filter独立执行此评估,并在图2(右)中绘制所得下降精度的分布。第二层大多数filters对准确度的贡献不到1%,而对于第一层的filters,有一个很长的范围。有些filters很重要,精度超过4%,但大多数filters约为1%。这意味着即使是一个微小且性能不佳的网络也可以进行过滤修剪而不会显著降低性能。该模型没有有效地分配filters来捕获必要特征的更广泛表示。图2(左)显示了两个层filters激活(CCA)的线性组合的相关性。很明显,在两个层中filters激活之间存在显著的相关性,其中几个接近1的亮黄色斑点有接近完美的相关性。第二层(右上对角线)比第一层(右下)的特征具有更多的重叠。对于随机正交矩阵,任何高于0.3(比深蓝色浅的点)的值都是异常。如果将线性组合扩展到核函数[45]或奇异值[30],则激活值将会更相关。不管怎么样,只要能说明对于卷积filters的标准训练不能最大化网络的潜在表示就足够了。

4.我们的训练Scheme:RePr
我们通过循环移除冗余filters,重新训练网络,重新初始化已删除的filters以及重复来修改训练过程。我们将每个filter(3D张量)视为一个单元,并将其表示为长向量 - ( f ) (f) (f)。设 M M M表示在 L L L层上分布有 F \mathcal{F} F个filters的模型。设 F ^ \hat{\mathcal{F}} F^表示 F \mathcal{F} F filters的子集,使得 M F M_{\mathcal{F}} MF表示完整网络,而 M F − F ^ M_{\mathcal{F}-\hat{\mathcal{F}}} MF−F^表示没有 F ^ \hat{\mathcal{F}} F^ filters的子网络。我们的训练Scheme是在训练完整网络 M F M_{\mathcal{F}} MF和子网络 M F − F ^ M_{\mathcal{F}-\hat{\mathcal{F}}} MF−F^之间交替进行。这引入了两个超参数。 第一个是在切换之前训练每个网络的迭代次数,整个网络用 S 1 S_1 S1表示,子网络用 S 2 S_2 S2表示。这两个数不能太小,以便每个网络都能学习并改进先前网络的结果。第二个超参数是重复该交替方案的总次数,用 N N N表示。N与特定范围的值无关,并且不需要调整。
我们算法中最重要的部分是用于对filters进行排名的度量标准。设 R \mathcal{R} R是将某个数值与filter相关联的度量。
这个值可以是权重的范数或其梯度或我们的度量标准——层中filter间的正交性。在这里,我们阐明我们的算法与度量的选择无关。当应用我们的训练Scheme时,对filter重要性的大多数合理选择都能比标准训练有所提高(见 第6节 Ablation 研究 )。
我们的训练Scheme是在宏观层面上运作,并不是一种权重更新规则。因此,不能替代SGD或其他适应性方法,如Adam [46]和RmsProp [47]。我们的Scheme适用于任何可用的优化器,并显示全面的改进。但是如果使用包含特定参数(如学习率)的优化器(如Adam),则被修剪过的filters ( F ^ \hat{\mathcal{F}} F^)的权重相对应的学习率需要进行重新初始化。相应的Batch Norm[48]参数 γ \gamma γ 和 β \beta β也必须重新初始化。出于这个原因,我们的训练Scheme与标准训练的比较是使用相同优化器完成的。
我们重新初始化filters( F ^ \hat{\mathcal{F}} F^) 使得它与被裁剪之前的值,和当前非裁剪filters( F − F ^ \mathcal{F}-\hat{\mathcal{F}} F−F^)的值正交。我们对来自同一层filters的权重使用QR分解来找到null空间并使用它来找到正交初始化点。
这里没有给出重新初始化filters的具体步骤和表达公式,对于复现是一个很大的问题,算是一个缺陷吧(●—●)
我们的算法是插入Re-initializing和Pruning - RePr(发音为:reaper)进行训练。 我们在算法1中总结了我们的训练方案。

我们使用浅层模型来分析我们训练Scheme的动态变化及其对训练/测试精度的影响。浅模型可以为每个filter计算greedy Oracle排名。这将使我们能够单独了解训练Scheme的影响,而不会因排名标准的影响而混淆结果。我们在第8节中提供了更大更深的卷积网络的结果。
考虑一个n层普通ConvNet,没有skip或dense连接,每层都有X个filters,如下所示:
I m g ⟶ [ C O N V ( X ) ⟶ R E L U ] n ⟶ F C ⟶ S o f t m a x Img \longrightarrow [CONV(X) \longrightarrow RELU]^n \longrightarrow FC \longrightarrow Softmax Img⟶[CONV(X)⟶RELU]n⟶FC⟶Softmax
我们将此架构表示为 C n ( X ) C^{n}(X) Cn(X)。因此, C 3 ( 32 ) C^{3}(32) C3(32)具有96个滤波器,并且当用SGD训练并且学习率为0.01时,实现73%的测试精度。图1显示了训练集(左)和测试集(右)的准确性图。在这个例子中,我们使用RePr训练Scheme, S 1 S_1 S1 = 20, S 2 S_2 S2= 10, N N N = 3, p % p% p%= 30,排名标准 R \mathcal{R} R为greedy Oracle。我们从训练集中抽取单独的5K张图像验证集来计算Oracle排名。在训练图中,注释[A]显示首次修剪过滤器的点。注释[C]标记此时模型的测试精度。[C]点测试精度的下降低于[A]点的训练精度,这并不令人意外,因为大多数模型都对训练集过拟合。但是,[D]的测试精度与[C]相同,但此时,模型只有70%的filters。这并不是一个令人惊讶的结果,因为对filter修剪的研究表明,在较低的修剪率下,大多数(如果不是全部)性能都可以恢复[9]。
令人惊讶的是,[E]处的测试精度,即重新引入修剪filters后的几个epochs,明显高于点[C]。[C]和[E]都是相同容量的网络,[E]处的更高精度不是由于模型收敛。在标准训练(橙色线)中,测试精度在此期间不会改变。不幸的是,那些首先grow网络然后修剪[49,50]的模型已经不再适应另一个增长phase,从而不能提高性能。在他们的回应中,这种技术破坏了通过修剪获得更小网络这个目的。然而,如果我们继续进行另外两次RePr的迭代训练,我们看到原始70%filters的点[F]产生的精度与点[E](100%的模型尺寸)相当。
我们可以从图中得出的另一个观察结果是RePr模型的训练精度较低,这表明模型上存在某种形式的正则化。这在图4(右)中很明显,它显示了具有大量迭代(N = 28)的RePr。 虽然较高的测试精度的边际收益(marginal benefit)迅速减少,但训练和测试精度之间的泛化差距(generalization gap)显著降低。
5.我们的度量:filter间的正交( inter-filter orthogonality)
搜索用于排列最不重要的filters的度量标准的原因有二 ,(1)对于大型网络来说计算greedy Oracle是不可行的,(2)greedy Oracle可能不是最好的标准。如果有一个捕获unique方向的filter(因此无法通过其他filters的线性组合替换)对精度的贡献较低,则Oracle将删除该filter。在随后的重新初始化和训练中,我们可能无法得到相同的方向集合。
激活模式捕获的方向表达了深度网络的容量[51]。制作正交特征将最大化捕获的方向并因此最大化网络的表现力。在密集连接的层中,正交权重导致正交特征,即使在ReLU [42]中也存在。但是,目前尚不清楚如何计算卷积层的正交性。
卷积层由分组到空间内核中的参数组成,并且稀疏地共享传入的激活。单个卷积层中的所有参数是否应同时考虑正交性?促进初始化正交的权重这一理论是基于FC层的,并且流行的深度学习库遵循本指南1,将卷积层视为一个忽略稀疏连通性的巨型向量。最近在[41]中描述了研究卷积filters正交性的尝试,但他们的动机是让非常深的网络(10K层)收敛而不是特征的正交性。我们的实证研究表明,强烈建议在层(层内filter间)而不是单个内核中要求各个filters的正交性。
指南1:tensorflow:ops/init ops.py#L543 & pytorch:nn/init.py#L350
内核大小为k×k的filter通常是形状为k×k×c的3D张量,其中c是输入激活中的通道数。将该张量展开为大小为k * k * c的1D向量,并用 f f f表示。用 J l J_l Jl表示层 l l l中的filters数量, l ∈ L l \in L l∈L, L L L是ConvNet中层的数量。让 W l W_l Wl为一个矩阵,则 W l W_l Wl每一行表示层 l l l中展开的filters ( f ) (f) (f)。
让 W ^ l = W l ∣ ∣ W l ∣ ∣ \hat{W}_l=\frac{W_l}{||W_l||} W^l=∣∣Wl∣∣Wl表示归一化的权重。则测量层 l l l中filter f f f的正交性(用 O l f O^f_l Olf表示)的计算公式表示如下:
(1) P l = ∣ W ^ l × W ^ l T − I ∣ P_l=|\hat{W}_l \times \hat{W}^T_l -I|\tag{1} Pl=∣W^l×W^lT−I∣(1)
(2) O l f = ∑ P l [ f ] J l O^f_l=\frac{\sum{P_l[f]}}{J_l}\tag{2} Olf=Jl∑Pl[f](2)
我不理解 W ^ l = W l ∣ ∣ W l ∣ ∣ \hat{W}_l=\frac{W_l}{||W_l||} W^l=∣∣Wl∣∣Wl这个归一化方式,感觉应该是进行均值为0方差为1的归一化操作,这样公式里面的单位矩阵也能解释了。
论文里没说 I I I是啥┓( ´∀` )┏,一开始我以为是对角线为1的单位矩阵,但是想想按照上面归一化的方式计算上又不对,我猜作用应该是减去对角线元素,使之为0
P l P_l Pl是一个大小为 J l × J l J_l \times J_l Jl×Jl矩阵, P [ i ] P[i] P[i]表示第 i t h i^{th} ith行的 P P P。第i行非对角线元素的 P P P表示其他filter对第 i i i个filter的投影,可以理解为相关性。当其他filters与该给定filter正交时,行的总和最小。如果此值在网络中的所有filters中最大,则我们将该filter排名为最不重要(因此需要进行修剪)。我们在单个层上计算filter的度量,在整个网络中对所有filters计算排名。我们不强制执行每层排名,因为这需要每个层学习都学习一个超参数p%,而某些层比其他层更敏感。与较浅的层相比,我们的方法从更深的层中修剪更多filters。 这与给定网络中每个滤波器的贡献分布一致(图2右)。
计算这个metric是在一个layer内,但rank是在所有layer进行的,目的是为了不让layer这个因数影响filter的rank,避开layer的差异性,同时也不引入过多的超参。
计算我们的度量不需计算Hessian [22]矩阵的逆或者二阶导数[23],并且对于任何大小的网络都是可行的。最昂贵的计算是尺寸为 J l × J l J_l \times J_l Jl×Jl的 L L L矩阵乘积,但GPU本来就是设计用于快速矩阵乘法。尽管如此,我们的方法比计算权重范数或激活或零点的平均百分比(Average Percentage of Zeros,APoZ)更昂贵。
鉴于filters的正交性的选择,一个显而易见的问题是询问是否在损失函数中添加软惩罚可以改善这种训练?一些研究人员[35,36,37]报道了用于任务特定的ConvNets模型中由于增加正规化而导致的边际改进。我们通过在损失函数中加入 λ ∗ ∑ l P l λ* \sum_l{P_l} λ∗∑lPl进行实验,但我们没有看到任何改进。软正则化(Soft regularization)惩罚所有filters并改变损耗surface以鼓励权重中的随机正交性但并没有提高表达性。
6.Ablation研究
修剪标准的比较(Comparison of pruning criteria)我们衡量我们的度量标准与Oracle的相关性来回答问题 - 我们的filter重要性排名指标有多好。我们度量标准(简称Ortho)与Oracle的Pearson correlation为0.38。然而,这并不是一个强相关性,当我们将其与其他已知指标进行比较时,它是最接近的。Molchanov等人[9] 报告他们的标准(泰勒)与greedy Oracle的Spearman correlation为0.73。我们在早期的epochs中发现相似数字的泰勒排名,但随着模型收敛相关性显著减小。这是由于已经收敛的filters的梯度值很低。泰勒度量是激活与梯度的乘积。在学习的早期阶段,高梯度与重要filters相关,但是当模型收敛时,低梯度并不一定意味着较少的突出的权重。可能是filter已经收敛到一个有用的特征,该特征不会导致模型的整体误差或卡在鞍点上。根据激活的范数,这种关系是相反的。因此,通过将这些术语相乘以实现平衡。但是我们的实验表明,在完全收敛的模型中,低梯度主导着高激活。因此,随着模型收敛,泰勒项将具有较低的值,并且将不再与低效filters相关联。虽然这些值的相关性表示指标在多大程度上可以代替预测精度,但更重要的是测量filters排名的相关性。值的相关性和排名的相关性可能不相同,但排名的相关性是更有意义的测量,因为它确定较弱filters。在filters的排名上测量时,Ortho与Oracle的相关性为0.58。其他指标使用排名显示非常差的相关性。图3(左侧和中间)显示了Oracle的各种指标的相关性图。图3右侧的表格显示了各种排名指标在CIFAR-10的测试精度。从表中可以看出,与标准训练和其他排名标准相比,正交性排名显著提高了准确性。

修剪filters的百分比我们训练Scheme的关键因素之一是在每个修剪阶段修剪filters的百分比(p%)。它的行为类似于Dropout参数,并影响模型的训练时间和泛化能力(见图4)。通常,修剪百分比越高,性能越好。然而,超过30%后表现并不明显。当高达50%时,该模型似乎从filters的丢弃中恢复。 除此之外,训练不稳定,有时模型无法收敛。
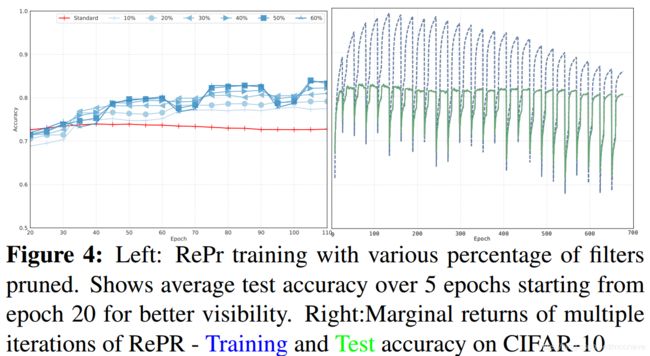 RePr迭代次数我们的实验表明,RePr过程的每次重复都会有收益递减,因此应限制为一位数(见图4(右))。类似于Dense-Sparse-Dense [18]和Born-Again-Networks [20],我们观察到对于大多数网络,两到三次迭代就足以实现最大的收益。
RePr迭代次数我们的实验表明,RePr过程的每次重复都会有收益递减,因此应限制为一位数(见图4(右))。类似于Dense-Sparse-Dense [18]和Born-Again-Networks [20],我们观察到对于大多数网络,两到三次迭代就足以实现最大的收益。
没看懂图4-右,不知道曲线具体表示的含义 ̄□ ̄||
优化器和S1/S2 图5(左)显示了使用不同优化器时的改进差异。我们的模型适用于大多数知名的优化器。Adam和Momentum表现优于SGD,因为他们在训练中增加了稳定性。我们尝试了S1和S2的各种值,如果它们中的任何一个足够大以使模型暂时收敛,则没有太大区别。

学习率计划具有固定学习率的SGD通常不会产生最佳模型性能。相反,已知在训练过程中逐渐降低学习率可以产生具有更高测试精度的模型。ResNet,DenseNet,Inception的最新结果均以预设的学习率计划产生。然而,学习率计划的选择本身就是一个超参数,需要针对每个模型进行专门调整。Cyclical learning rates [52]可以提供更强的性能,而无需详尽的调整精确的学习率计划。图6显示了我们的训练技术与固定schedule learning rate和cyclical learning rate结合使用时的比较。我们的训练Scheme不受使用这些计划的影响,并且比标准训练的改进仍然很明显。

Dropout的影响 Dropout虽然通常应用于多层感知器,但通常不用于ConvNets。我们的技术可以被视为一种非随机Dropout,十分适用于ConvNets。与标准Dropout不同,我们的方法作用于整个filter而不是单个权重,并且仅在训练的选定阶段而不是在每个训练步骤中应用。Dropout通过鼓励权重的共同适应来防止过度拟合。这在过度参数化模型的情况下是有效的,但在紧凑或浅模型中,Dropout可能会不必要地减少已经有限的模型容量
Dropout在使用的时候不就是让整个filter为0吗?不明白为什么说是作用于单个权重上o((⊙﹏⊙))o

图7显示了标准训练和我们提出的方法(RePr)在三层卷积神经网络上有和没有Dropout的性能,每层网络有32个滤波器。Dropout的概率为0.5。 我们观察到,由于模型的有效容量减少一半,包含Dropout会降低最终的测试精度。无论是否添加标准Dropout,我们的方法都可以提高性能,证明其效果与Dropout的优势不同。
正交损失-OL将filters的正交性(公式1)作为正则化项使其成为优化器损失的一部分不会显著影响模型的性能。因此,损失函数将是:
L = C r o s s _ e n t r o p y + λ ∗ ∣ W ^ l × W ^ l T − I ∣ L=Cross\_entropy + \lambda * |\hat{W}_l \times \hat{W}^T_l -I| L=Cross_entropy+λ∗∣W^l×W^lT−I∣
这里我感觉损失项应该是 λ ∗ ∑ L ∣ W ^ l × W ^ l T − I ∣ \lambda * \sum_L{ |\hat{W}_l \times \hat{W}^T_l -I|} λ∗∑L∣W^l×W^lT−I∣也就是第5章提到的 λ ∗ ∑ l P l \lambda * \sum_lP_l λ∗∑lPl
其中, λ \lambda λ是一个超参数,它平衡两个损失项。我们尝试了各种 λ \lambda λ值。 表1报告了该损失项对于 λ = 0.01 \lambda = 0.01 λ=0.01的结果,其验证准确度最高。 OL指的是此损失项的添加。

7.正交与蒸馏(Orthogonality and Distillation)
我们的方法,RePr和知识蒸馏(KD)都是提高紧凑模型性能的技术。RePr减少了过滤器表示的重叠,KD从更大的网络中提取信息。我们对这些技术进行了简要比较,并表明它们可以结合起来以实现更好的性能。

RePr使用inter-filter正交性重复地丢弃在权重方向上具有最多重叠的filters,如公式2所示。因此,我们希望这个值在训练期间逐渐减少。图8(左)显示了三种训练方案下整个网络该值的总和。我们使用Ortho和Oracle两种不同的filter排名标准来展示RePr。使用Ortho排名的RePr训练方案具有最低的Ortho总和。与标准训练相比,令人惊讶的是,使用Oracle排名的RePr训练也减少了filter重叠。一旦模型开始收敛,基于Oracle排名的最不重要的filters是重叠最多的filters。丢弃这些滤波器可以提高测试精度(图3右侧的表格)。这种改进是否与知识蒸馏来自相同的来源?知识蒸馏(KD)是一种用于训练紧凑模型的成熟方法。与标准训练相比,使用来自teacher的soft logits 和ground truth信号,模型能收敛到更好的最佳状态。如果我们将KD应用于相同的三个实验(见图8,右),我们看到所有模型都具有明显更大的Ortho和。甚至RePr(Ortho)模型也在努力降低总和,因为模型被强烈引导收敛到特定的解决方案。这表明是由KD引起的提高而不是由于减少了filter重叠。因此,同时使用这两种技术的模型应该通过更好的泛化而受益。实际上,情况正是如此,因为组合模型的性能明显优于单个模型,如表2所示。

8.结果
我们在不同的ConvNets [53,1,29,54,31]上展示了我们的训练方案RePr和我们的排名标准inter-filter 正交性Ortho的性能。对于所有提供的结果,RePr参数是: S 1 = 20 S_1=20 S1=20, S 2 = 10 S_2 = 10 S2=10, p % = 30 p%= 30 p%=30,并且具有三次迭代 N = 3 N = 3 N=3。
我们在表3中将我们的训练方案与其他类似方案如BAN和DSD等进行了比较。所有三种方案都经过三次迭代训练,即 N = 3 N = 3 N=3。所有模型都经过150个epochs训练,具有相同的学习率Schedule和初始化方法。DSD和RePr(权重)执行大致相同的功能 - 按magnitude对模型进行稀疏,差异在于DSD作用于单个weights,而RePr(权重)作用于整个filters。因此,我们观察到这些技术之间相似的性能。RePr(Ortho)优于其他技术并且与BAN相比训练成本更低,因为BAN需要N个完整的训练cycles。

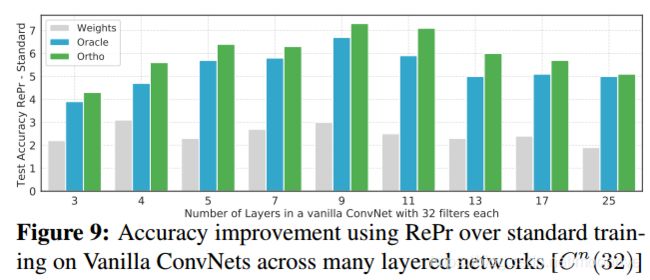
与现代架构相比,普通的ConvNets在其特征表示的分配上显示出更低的效率。因此,与现代架构相比,把我们的方法应用于普通ConvNets有更大的提高。表4显示了在CIFAR 10和100上的测试错误。与DenseNet或ResNet相比,每层具有32个filters的普通CNN具有较高误差,但它的推理时间明显更短。RePr训练使CIFAR-10的普通CNN相对准确度提高了8%,CIFAR-100提高了25%。基线DenseNet和ResNet模型的性能仍然优于使用RePr训练的普通CNN,但这些模型的推理成本是其两倍多。为了进行比较,我们还考虑仅使用5层的简化DenseNet模型,其具有与3层普通ConvNet相似的推理时间。该模型比普通ConvNet具有更少的参数(乘以11倍)导致错误率显著提高,但由于在许多实际应用中推理时间更为重要,我们选择统一的推理时间而不是参数数量。图9显示了具有不同深度的普通CNN的更多结果。普通CNN随着深度加深开始过度拟合数据,因为大多数filters会收敛类似的表示。我们的训练方案迫使它们不同,这减少了过度拟合(图4右)。在CIFAR-10上使用18层的普通CNN与3层CNN相比具有更大的测试误差。但通过RePr训练,18层模型显示较低的测试错误。

RePr还能够改善ResNet和浅层DenseNet的性能。这种改进在CIFAR-100上更大,因为它是100个类别的更难的分类任务,并且需要更specialized的filters。同样,我们的训练Scheme在ImageNet上显示出更大的相对改进,这是一种1000个类别的分类问题。表5列出了在ImageNet [55]上各种ConvNets使用标准训练和RePr训练的 top-1 test error。RePr应用三次(N = 3),表格显示每轮后的错误。我们使用建议的超参数尽可能复现已知模型的结果,最终得到的模型与公开模型的误差在±1%范围内。补充材料中提供了训练和超参数的更多细节。表中每轮RePr都可以提高性能并显著降低returns。在没有skip连接并且具有较低的基线性能的结构(如Inception v1和VGG)中改进更加明显。

我们的模型改进了使用类似ConvNets的其他计算机视觉任务。我们提供了一些视觉问答和目标检测任务的结果样本。这两项任务都涉及使用ConvNets提取功能,RePr可以改善其基线结果。
视觉问答在视觉问答(VQA)领域,模型的输入是一张图像和与图像有关的问题(作为文本),必须产生该问题的答案。解决此问题的大多数模型使用标准ConvNets来提取图像特征,使用LSTM网络来提取文本特征。然后将这些特征输入到第三个模型,该模型学习选择正确的答案作为分类问题。最先进的模型使用注意力层和复杂的特征映射。我们尝试了一种更标准的模型,其中图像特征和语言特征被输入到多层感知机,最后一个softmax层对候选答案进行1000路分类。表6提供了使用VQA-LSTM-CNN模型[56]的VQAv1的准确性。并报告了开放式问题的结果,与多项选择问题相比,这是一项更难的任务。我们从使用标准训练和RePr(Ortho)训练的Inception-v1中提取图像特征,然后把图像特征和从问题中提取的语言embeddings (GloVe向量) 提供给两层全连接网络。因此,结果6中两个报告之间的唯一区别是Inception-v1的训练方法。

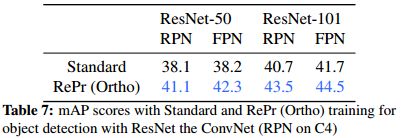
目标检测对于目标检测,我们使用在ImageNet上预训练的ResNet 50和101模型在Faster R-CNN上进行实验。我们使用c4卷积层对特征金字塔网络和基线RPN进行了实验。我们使用Tensorpack [57]的模型结构,它能够重现报告的mAP分数。该模型接受了COCO数据集“trainval35k + minival”拆分(2014年)的训练。平均精度均值(mAP)计算为10个IoU阈值,从0.5到0.95。通过标准训练和RePr训练获得的boxes的mAP显示在表7中。
9.结论
我们介绍了RePr,一种循环百分比丢弃最低表达的filters并重新学习的训练方法。在删除这些filters之后,修剪的子模型能够使用剩余参数重新捕获丢失的特征,一旦重新引入filters,就可以更加稳健和有效地分配模型容量。我们表明,在重新引入filters之前,减少的模型需要训练,并且仔细选择该训练持续时间会带来显著的收益。我们还证明了这个过程可以通过递减收益来实现。先前的研究强调CNN学习的特征表示十分低效,受此启发我们引入了一种新的inter-filter正交性度量,用于在RePr训练中对filter重要性进行排序,并证明该度量优于现有的排序度量。我们的训练方法能够通过高效使用有限容量来显著提高参数不足网络的性能,并且性能提升是知识蒸馏的补充。即使在复杂的,过度参数化的网络架构的情况下,我们的方法也能够提高各种任务的性能。
附录
ImageNet训练细节
训练大型模型,如ResNet,VGG或Inception(如表4所述)可能很困难,并且模型可能并不总是在训练运行中收敛到类似的最佳值。通过我们的RePr训练Scheme,我们观察到重新引入丢弃的filters时,大的 p % p% p%值有时会产生崩溃。在分析中,我们发现这是由于新初始化的filters的大量随机激活导致的。 这可以通过用相对较小的值初始化新filters来克服。
最小化此问题的另一个技巧是为给定filter重新初始化下一层的相应内核。考虑第 l l l层的filter f f f。 来自此filter f f f的激活将成为下一层 l + 1 l+1 l+1每个filter的内核的输入。如果filter f f f被修剪,然后重新初始化,那么层 l + 1 l+1 l+1中的所有内核也应该初始化为小的随机值,因为他们学习的特征已经不再存在。这可以防止这些内核(目前是随机的)新的激活主导其他内核的激活。
在一次迭代中修剪大量filters可能导致训练不稳定。这主要是由于BatchNorm参数的运行均值/方差的变化。为了解决这个问题,可以通过多个小批量修剪filters。没有必要重新评估排名,因为它几次迭代时没有显著变化。DenseNet中的训练不稳定是由dense connections导致的。删除多个filters会导致前向dense connections发生重大变化,并且会影响所有现有的激活。解决此问题的一种方法是在从网络中移除filters之前,将filter权重在多次迭代中衰减到非常小的范数。类似地,Squeezeand-Excitation Networks也难以修剪,因为它们维持了来自所有filters激活的已学习的缩放参数。与BatchNorm不同,删除相应的缩放参数并非易事,因为它们是全连接层的一部分。删除此值将更改网络结构以及所有其他激活的相对缩放。
也可以将RePr应用于预先训练的模型。 这对ImageNet尤其有用,因为从头开始训练成本很高。将RePr应用于预训练模型能够产生一些改进,但不如在整个训练中应用RePr有效。必须仔细选择微调学习速率,以尽量减少所需的训练时间。我们的实验表明,使用自适应LR优化器(如Adam)可能更适合从预训练的权重进行微调。
超参数
所有ImageNet模型都是使用Tensorflow和Tesla V100进行训练,模型定义从官方TF库(tensorflow/contrib/slim/python/slim/nets)获得。图像增加了亮度(0.6到1.4),对比度(0.6到1.4),饱和度(0.4),lightning(0.1),随机中心裁剪和水平翻转。在测试期间,在图像中心裁剪224×224上测试。大多数模型训练的batch size为256,但ResNet-101,ResNet-152和Inception-v2等大型模型的batch size为128。根据实现,RePr可能会添加自己的非训练变量,这将占用GPU内存,因此需要使用比论文最初报告的更小的batch size。batch size为256的模型使用SGD进行训练,前30个epochs的学习率为0.1,接下来的30个epochs为0.01,剩余epochs为0.001。对于batch size为128的模型,这些学习率相应地减少一半。对于ResNet模型,使用MSRA初始化(FAN OUT scaling=2.0)卷积层,并且使用Random Normal (标准偏差= 0:01)初始化全连接层。