数据结构及算法基础 之图 (六) 最小生成树

 
 

一、什么是最小生成树

  现在假设有一个很实际的问题：我们要在n个城市中建立一个通信网络，则连通这n个城市需要布置n-1一条通信线路，这个时候我们需要考虑如何在成本最低的情况下建立这个通信网？
  于是我们就可以引入连通图来解决我们遇到的问题，n个城市就是图上的n个顶点，然后，边表示两个城市的通信线路，每条边上的权重就是我们搭建这条线路所需要的成本，所以现在我们有n个顶点的连通网可以建立不同的生成树，每一颗生成树都可以作为一个通信网，当我们构造这个连通网所花的成本最小时，搭建该连通网的生成树，就称为最小生成树。

  构造最小生成树有很多算法，但是他们都是利用了最小生成树的同一种性质：MST性质（假设N=(V,{E})是一个连通网，U是顶点集V的一个非空子集，如果（u，v）是一条具有最小权值的边，其中u属于U，v属于V-U，则必定存在一颗包含边（u，v）的最小生成树），下面就介绍两种使用MST性质生成最小生成树的算法：普里姆算法和克鲁斯卡尔算法。

 

二、普里姆算法—Prim算法

算法思路：
  首先就是从图中的一个起点a开始，把a加入U集合，然后，寻找从与a有关联的边中，权重最小的那条边并且该边的终点b在顶点集合：（V-U）中，我们也把b加入到集合U中，并且输出边（a，b）的信息，这样我们的集合U就有：{a,b}，然后，我们寻找与a关联和b关联的边中，权重最小的那条边并且该边的终点在集合：（V-U）中，我们把c加入到集合U中，并且输出对应的那条边的信息，这样我们的集合U就有：{a,b,c}这三个元素了，一次类推，直到所有顶点都加入到了集合U。

 

三、代码实现

PrimGraph.h：

#ifndef __GRAPH__H
#define __GRAPH__H
 
/*邻接矩阵*/
#define MAX_VERTEX 100
typedef char  vertexType; /*顶点类型*/
typedef int  weightType;
//int visited[MAX_VERTEX]; /*for 遍历标记*/
  
  
/*邻接表*/
/*边节点结构*/
typedef struct _edgeNode {
    vertexType vertex; /*顶点*/
    weightType weight; /*权重*/
    struct _edgeNode *next;
} edgeNode_s, *edgeNode_p;
 
/*数组0结构*/
typedef struct _vertexGraph {
    vertexType vertex; 
    edgeNode_p fistNode;
}vertexGraph[MAX_VERTEX], vertexGraph_s;
 
typedef struct _adjListGraph {
    int numEdges, numVertex; /*顶点数与边数*/
    vertexGraph graph;
} adjListGraph_s, *adjListGraph_p;
 
 
#endif

PrimGraph.c

#include 
#include 
#include 
#include 
#include "graph.h"
 
//#define OrthogonalList
#define AdjList
#ifdef AdjList
 
 
/*根据顶点返回在数组中的位置*/
int locateGraph(adjListGraph_p adjGraph, vertexType c)
{
    int i;
     
    for (i = 0; i < adjGraph->numVertex; i++) {
        if (adjGraph->graph[i].vertex == c)
            return i;
    }
    return -1;
}
 
 
int printfGraph(adjListGraph_p adjGraph)
{
    int i;
    edgeNode_p p1,p2;
     
    for(i = 0; i < adjGraph->numVertex; i ++) {
        printf("%c->", adjGraph->graph[i].vertex);
        p1 = adjGraph->graph[i].fistNode;
        while(p1) {
            p2 = p1->next;
            printf("%c(%d),", p1->vertex, p1->weight);
            p1 = p2;
        }
        printf("\n");
    }
    return 0;
}
 
int crateAdjListGraph(adjListGraph_p adjGraph)
{
    int i, j, k, w;
    vertexType x,y;
    edgeNode_p edgeNode;
     
    if (!adjGraph)
        return -1;
         
    printf("input numEages:");
    scanf("%d", &(adjGraph->numEdges));
    printf("input numVertex:");
    scanf("%d", &(adjGraph->numVertex));
     
    if (adjGraph->numVertex > MAX_VERTEX)
        return -1;
         
    for (i = 0; i < adjGraph->numVertex; i++) {
        printf("input vertex:");
        adjGraph->graph[i].vertex = getchar();
        while(adjGraph->graph[i].vertex == '\n')
            adjGraph->graph[i].vertex = getchar();
    }
     
    for (k = 0; k < adjGraph->numEdges; k ++) {
        printf("input vertex and weight\n");
        x = getchar();
        while(x == '\n')
            x = getchar();
        y = getchar();
        while(y == '\n')
            y = getchar();
        scanf("%d", &w);
        /*邻接表*/
        i = locateGraph(adjGraph, x);
        j = locateGraph(adjGraph, y);
        if (i == -1 || j == -1) {
            printf("input error\n");
            k --;
            continue;
        }
        edgeNode = (edgeNode_p)malloc(sizeof(*edgeNode));
        if (!edgeNode)
            return -2;
        edgeNode->weight = w;
        edgeNode->vertex = y;
        edgeNode->next = adjGraph->graph[i].fistNode;
        adjGraph->graph[i].fistNode = edgeNode;
        /*无向图增加*/
#if 0
        edgeNode = (edgeNode_p)malloc(sizeof(*edgeNode));
        if (!edgeNode)
            return -2;
        edgeNode->weight = w;
        edgeNode->vertex = x;
        edgeNode->next = adjGraph->graph[j].fistNode;
        adjGraph->graph[j].fistNode = edgeNode;
#endif
#if 0       
        /*逆邻接表*/
        j = locateGraph(adjGraph, y);
        //j = locateGraph(adjGraph, y);
        if (j == -1) {
            printf("input error\n");
            k --;
            continue;
        }
        edgeNode = (edgeNode_p)malloc(sizeof(*edgeNode));
        if (!edgeNode)
            return -2;
        edgeNode->weight = w;
        edgeNode->vertex = x;
        edgeNode->next = adjGraph->graph[j].fistNode;
        adjGraph->graph[j].fistNode = edgeNode;
#endif
    }
     
    return 0;
}
 
 
/*边的结构*/
typedef struct _Edge {
    vertexType st; /*开始顶点*/
    vertexType end; /*结束顶点*/
    weightType weight; /*权重*/
} Edge;
 
 
/*最小生成树   prim（普里姆）算法*/
int Prim(adjListGraph_p adjGraph)
{
    int j, m, n;
    edgeNode_p e;
    Edge edge[adjGraph->numVertex];
    weightType min;
    int index;
     
    memset(edge, 0, sizeof(Edge) * adjGraph->numVertex);
    for (j = 0; j < adjGraph->numVertex; j++)
        edge[j].weight = INT_MAX;
         
    for (m = 0; m < (adjGraph->numVertex - 1); m ++) {
        min = INT_MAX;
        if (m == 0) index = m;
        e = adjGraph->graph[index].fistNode;
        edge[index].weight = -1;
        while (e) {
            j = locateGraph(adjGraph, e->vertex);
            if (edge[j].weight > e->weight) {
                edge[j].st = adjGraph->graph[index].vertex;
                edge[j].end = e->vertex;
                edge[j].weight = e->weight;
            }
            e = e->next;
        }
        for (n = 0; n < adjGraph->numVertex; n++) {
            if (edge[n].weight != -1) {
                if (min > edge[n].weight) {
                    index = n;
                    min = edge[n].weight;
                }
            }
        }
        printf("%c---->%c   %d\n",  edge[index].st, edge[index].end, min);
    }
     
    return 0;
}
 
#endif

 

四、示例测试

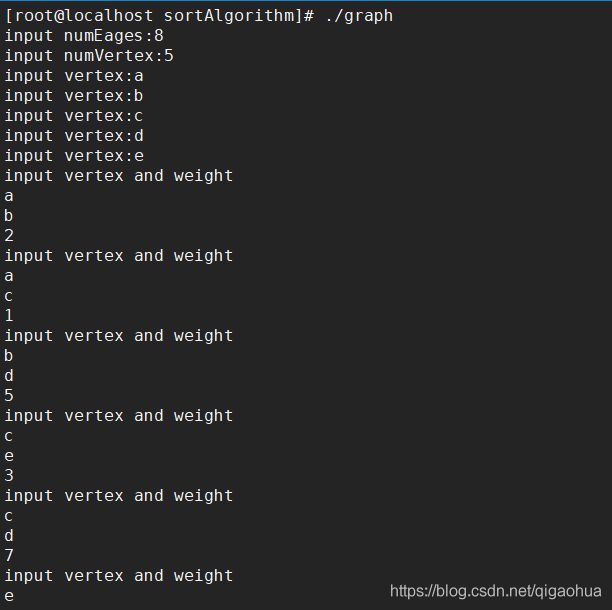
测试代码：

int main()
{
    adjListGraph_s g;
    memset(&g, 0, sizeof(g));
    crateAdjListGraph(&g);
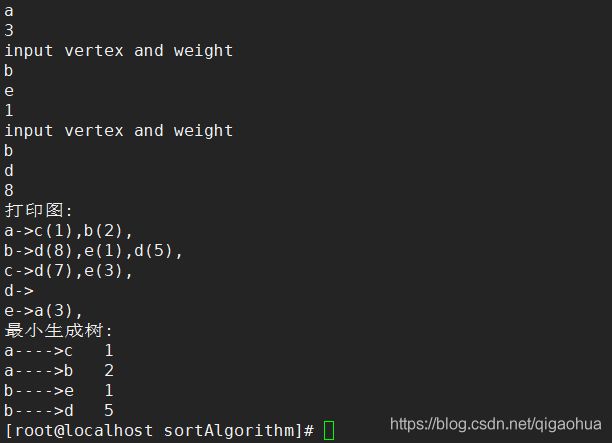
    printf("打印图:\n");
    printfGraph(&g);
    //printf("深度优先遍历:\n");
    //DFSAdjList(&g);
    //printf("广度优先遍历:\n");
    //BFSAdjList(&g);
    printf("最小生成树:\n");
    Prim(&g);
    return 0;
}

测试结果：

 
 
参考：https://blog.csdn.net/qq_35644234/article/details/59106779

 
 
 
 
 
 
 
关注公众号"小败日记"，搬砖过程遇到的问题，大家一起探讨，资源共享