机器学习 | 线性判别分析LDA和主成分分析PCA
LDA和PCA介绍
- 1 背景
- 2 线性判别分析LDA
- 2.1 含义
- 2.2 图解
- 2.3 数学原理
- 2.4 LDA降维流程
- 2.5 LDA用于分类
- 2.6 代码实现
- 3 主成分分析PCA
- 3.1 含义
- 3.2 图解
- 3.3 数学推导
- 3.3.1 基于最小投影距离推导
- 3.3.2 基于最大投影方差推导
- 3.3.3 总结
- 3.4 PCA的算法流程
- 3.5 代码实现
- 3.6 实例
- 3.7 优缺点
- 4 LDA和PCA有什么区别和联系？
- 参考
1 背景
聊到LDA，大部分可能都会想到是线性判别分析，甚至在面试的时候，我简历上明明写的是LDA主题模型，但面试官其实不太懂，直接就问了线性判别分析。。。所以今天我们就来聊一聊线性判别分析LDA以及和其很相近的PCA！
2 线性判别分析LDA
2.1 含义
- LDA的全称是Linear Discriminant Analysis（线性判别分析），是一种supervised learning。 - LDA的原理：将带上标签的数据（点），通过投影的方法，投影到维度更低的空间中，使得投影后的点，会形成按类别区分，一簇一簇的情况，相同类别的点，将会在投影后的空间中更接近。
- 投影后类内方差最小，类间方差最大。 要将数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。
2.2 图解
- LDA是将一个高维的点投影到一条直线上
- LDA追求的目标：给出一个标注了类别的数据集，投影到了一条直线之后，能够使得点尽量的按类别区分开
- 注：我们的原始数据一般也是超过二维的，投影后的也一般不是直线，而是一个低维的超平面。
当k=2即二分类问题的时候，如下图所示：
2.3 数学原理
- 找到损失函数！即投影后的点之间的不同类距离尽可能远，同一类之间尽可能接近！即投影后类内方差最小，类间方差最大！
那损失函数如何度量呢？直观来看，如果是分子=类间方差，分母=类内方差，则这个分数值越大越好！具体的数学表达式为：
于是我们的目标就变成了：求J最大时对应的W，也就是投影的权重！对应是直线的权重！
但直接求好像有点麻烦，我们进行相应的转换！
现在J变成了上面这样的形式，下面就可以用一个结论了！涉及到一个广义瑞利商的概念和相关结论：
一旦通过上述方式求出了w，也就知道了我们的最佳投影方向了！从而将数据进行了降维！
2.4 LDA降维流程
2.5 LDA用于分类
那除了做降维，LDA还可以干吗吗？还可以用于分类。分类原理为：
一个常见的LDA分类基本思想是：假设各个类别的样本数据符合高斯分布，这样利用LDA进行投影后，可以利用极大似然估计计算各个类别投影数据的均值和方差，进而得到该类别高斯分布的概率密度函数。当一个新的样本到来后，我们可以将它投影，然后将投影后的样本特征分别带入各个类别的高斯分布概率密度函数，计算它属于这个类别的概率，最大的概率对应的类别即为预测类别。
2.6 代码实现
详情见刘建平老师博客：https://www.cnblogs.com/pinard/p/6249328.html
直接调用Python中sklearn对应的接口即可！
3 主成分分析PCA
3.1 含义
PCA全名是Principle Component Analysis，即主成分分析。是一种重要的降维方法。希望将数据从n维降到m维，而让这m维数据尽可能代表原始数据集，同时希望损失尽可能的小。
3.2 图解
下面是一堆二维数据集，希望能降成一维，请问是按照u1的方向还是u2的方向进行投影降维呢？直观上会觉得u1更好！原因是啥呢？
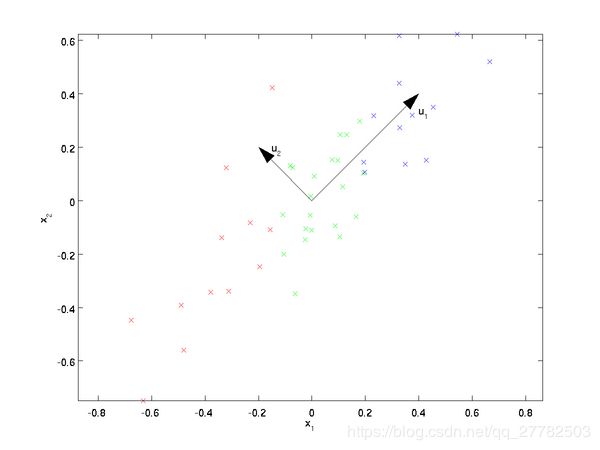
- 理由1：在u1方向上投影更加的分散，数据的方差更大。即样本点在这个直线上的投影能尽可能的分开。
- 理由2：在u1方向投影后原始数据离这个轴的距离之和更近一些！即样本点到这个直线的距离足够近。
3.3 数学推导
3.3.1 基于最小投影距离推导
这部分参考刘建平老师的博客，看着很多数学式子，但静下心来看，发现是不难的。
3.3.2 基于最大投影方差推导
3.3.3 总结
通过上面两种推导，我们就可以发现，核心是只要求出样本点的协方差矩阵对应的特征值和特征向量就ok了！算出前m个特征值（贡献率一般达到85%以上）以及其对应的特征向量，然后将特征向量乘以原始的数据x就可以实现降维了！
3.4 PCA的算法流程
大致有下面几步：
- 中心化处理
- 计算样本的协方差矩阵
- 求矩阵的特征值和特征向量
- 根据方差贡献率看选几个主成分
- 进行主成分的表达式对原始数据进行降维处理，形成了主成分，后续对主成分进行进一步分析！
3.5 代码实现
具体见刘老师博客：https://www.cnblogs.com/pinard/p/6243025.html
3.6 实例
3.7 优缺点
优点：
- 仅仅需要以方差衡量信息量，不受数据集以外的因素影响。
- 各主成分之间正交，可消除原始数据成分间的相互影响的因素。
- 计算方法简单，主要运算是特征值分解，易于实现。
缺点：
- 主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。
- 方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。
4 LDA和PCA有什么区别和联系？
1、联系：
- 都是降维方法，即两者均可以对数据进行降维。
- 两者在降维时均使用了矩阵特征分解的思想
- 两者都假设数据符合高斯分布
2、区别：
- PCA是无监督的，LDA是有监督的
- LDA不适合对非高斯分布样本进行降维，PCA也有这个问题。
- LDA降维最多降到类别数k-1的维数，如果我们降维的维度大于k-1，则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
- LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好。
- LDA可能过度拟合数据。
- LDA是作为独立的算法存在，PCA更多的用于数据的预处理的工作。
参考
- LDA讲的不错：https://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html
- 刘建平 https://www.cnblogs.com/pinard/p/6244265.html
- PCA原理 知乎：https://zhuanlan.zhihu.com/p/21580949