设置开发集的必要性、偏差、方差

设置开发集的必要性

通过不断开设新的数据集来逐渐减轻过拟合的程度

开发集：寻找好的超参数，模拟测试集防止模型过拟合训练集。

开发集（重要性）：作用在于模拟测试集，而测试集的最大特点就是未知，即在训练过程中是见不到的。正因为开发集和测试集在训练过程中都是未知的，你才可以说，如果你的超参数适用于验证集，那么它们也大概会适用于测试集。

开发集与测试集应尽量是同分布的

当我们训练完成一个分类器，并想把它应用到实践的，可能遇到在训练的过程中效果很好，但是在实践的过程中效果非常差，这种情况说明我们训练分类器的数据集的分布和我们实践过程的数据的分布不同，导致算法的泛化能力很差。

开发集和测试集数据分布不同将会导致开发的系统在开发集上表现良好，但在测试集上却表现不佳。这种情况下解决方案就不那么明确了，此时可能存在以下一种或者多种情况：

1. 在开发集上过拟合了；

2. 测试集比开发集更难进行预测，尽管算法做的足够好，却很难有进一步的改进空间；

3. 测试集不一定比开发集更难进行预测，但与开发集的性质不同(分布不同)。因此在开发集上表现良好的算法，不一定在测试集上也能够表现良好，如果是这种情况，大量改进开发集性能的工作将会是徒劳的。

在开发集上反复评估想法的过程导致算法逐渐对开发集“过拟合”。当完成开发后，你将在测试集上评估你的算法。如果你的算法在开发集上的表现远好于在测试集上的表现，这意味着你已经过拟合开发集。这种情况下，更新开发集。 如果你需要跟踪团队的进度，你也可以在测试集上定期评估你的系统——每月或每周一次。但不要使用测试集来对算法做任何决定，包括是否回滚到上一周的系统。如果这样做，你将开始过拟合测试集，并且不能再依靠它来完全无偏见的评估系统的性能（你可能会在发表研究论文或做出重要商业决策是使用这个指标）。

总结：
1.从分布中选择开发集和测试集，该分布反映你期望在未来获得什么样的数据，并希望在上面做得很好。这可能和你训练数据的分布不一样。
2. 如果可能的话，选择来自同一分布的开发集和测试集。
3. 为你的团队选择单一数字的评估指标进行优化。如果你关心多个目标，考虑把它们合并到一个公式中（例如平均多个错误指标），或设定满足指标和优化指标。
4. 机器学习是一个高度迭代的过程：在发现你满意的方法之前你可能需要尝试很多的idea。
5. 开发/测试集和单一数字评估指标可以帮助你快速评估算法，从而迭代的更快。
6. 当开始一个全新的应用时，尝试快速建立开发/测试集和评估指标，最好在一周之内。当然，在成熟应用上花费更长的时间是ok的。
7. 当你拥有大量数据时，依据70%：30%的比例划分训练/测试集这一经验性的方法不太适用；开发/测试集可以占远小于30%的数据量。
8. 你的开发集应该足够大，以检测出算法准确性有意义的改变，但没必要更大。你的测试集应该足够大，大到能对你的系统整体性能有一个确信的评估。

key：
如果你的开发集和评估指标不再使你的团队在正确方向上前进，快速改变它们：（i）如果你过拟合了开发集，去获得更多的开发集数据。（ii）如果你所关心的实际分布和开发/测试集的分布不同，那么去获得新的开发/测试集数据。（iii）如果你的评估指标不再能衡量对你来说最重要的东西，改变评估指标。

与其给算法所有可用的训练数据，不如将其分成两个子集：算法用于训练的实际训练集，和一个独立的数据集，我们称之为“训练开发”集，不用于训练。
现在你有四个数据子集：
训练集：这是算法将从中学习的数据（例如互联网图片和移动图片）。这不必从我们真正关心数据的相同分布（开发/测试集分布）中获取。
训练开发集：该数据和训练集来自相同的分布（即互联网图片和移动图片）。通常比训练集要小，它只需要足够大以评估和跟踪学习算法的进度就行。
开发集：和测试集来自相同的分布，它反映我们最终关心并想要做好的数据的分布（即移动图片）。
测试集：和开发集来自相同的分布（例如移动图片）。

有以上四个独立的数据集，现在你可以评估：
训练错误，通过对训练集进行评估。
算法泛化到和训练数据来自相同分布的新数据的能力，通过对训练开发集进行评估。
算法在你关心的任务上的表现，通过对开发、测试集进行评估。

偏差： 在训练集上的错误率
方差： 在开发集上的错误率-训练集上的错误率

如果方差值是负的，你在训练集上的表现比最优错误率要好。这意味着你正在过拟合训练集，并且算法已经过度记忆（over-memorized）训练集。你应该专注于方差减少的方法，而不是进一步减少偏差的方法。

（偏差较大，方差较小） ---------欠拟合
（偏差较小，方差较大） ---------过拟合
（偏差较大，方差较大） ---------同时过拟合和欠拟合

最优错误率（不可避免的偏差）：“最优”的系统的错误率
可避免的偏差 = 通过训练的错误率 - 最优错误率
**偏差 **= 最佳错误率（不可避免偏差）+ 可避免偏差

了解最优错误率有利于指导我们的后续步骤。在统计学上，最优错误率也被成为贝叶斯错误率（Bayes error rate），或贝叶斯率

我们如何才能知道最优错误率是多少呢？对于人类还算擅长的任务，例如识别图片或转录音频剪辑，你可以要求人们提供标签，然后测量人为标签相对于你训练集的准确率。这将给出最优错误率的估计。如果你正在解决甚至人也很难解决的问题（例如预测推荐什么电影，或向用户展示什么广告），这将很难估计最优错误率。

减少可避免偏差的方法

如果你的学习算法遭受高可避免偏差，你可以尝试以下方法：

1. 增加模型大小（如神经元/层的数量）：该方法可以减少偏差，因为它可以让你更好的适应训练集。如果你发现该方法增加了方差，那么使用正则化方法，它通常能够消除方差的增加。
2. 基于错误分析的洞察修改输入特征：假设错误分析启发你去创建额外的特征，以帮助算法消除特定类别的错误。（我们在下一章节进一步讨论）这些新特征可能有助于减少偏差和方差。理论上来说，增加更多的特征可能会增加方差，但如果你发现这种情况，那么久使用正则化方法，它通常能够消除方差的增加。
3. 减少或消除正则化（L2正则化，L1正则化，dropout）：这将减少可避免偏差，但会增加方差。
4. 修改模型架构（如神经网络架构）以便更适合你的问题：这种方法能够影响偏差和方差。
   一种没有帮助的方法：
   增加更多训练数据：这种方法有助于解决方差问题，但是它通常对偏差没有显著的影响。

减少方差的方法

如果你的学习算法遭受高方差，你可以尝试以下方法：

1. 添加更多训练数据：只要你能够获取更多的数据和处理这些数据的充足计算能力，这是处理方差问题最简单也是最可靠的方法。
2. 添加正则化（L2正则化，L1正则化，dropout）：该方法减少了方差，但增加了偏差。
3. 添加提前停止（early stopping）（基于开发集错误提前停止梯度下降）：该方法减少方差但增加了偏差。提前停止的行为很像正则化方法，一些作者称它为正则化方法。
4. 选择特征以减少输入特征的数目/类型：该方法可能有助于解决方差问题，但也可能增加偏差。略微减少特征数量（比如从1000个特征减少到900）不太可能对偏差产生很大影响。显著地减少它（比如从1000减少到100——减少10倍）更可能有显著的影响，只要你没有将太多有用的特征排除在外。在现代深度学习中，当数据丰富时，已经从特征选择转移了出来，现在我们更有可能给算法我们所有的特征，并让算法根据数据分类使用哪些特征。但是当你训练集比较小时，特征选择可能非常有用。
5. 减少模型大小（如神经元/层的数量）：谨慎使用。该方法能够减少方差，但可能增加偏差。但是，我不推荐使用该方法来处理方差。减少模型大小的好处就是降低计算成本，从而加快训练模型的速度。如果加快模型的训练是有用的，那无论如何考虑减少模型的大小。但是如果你的目标是减少方差，并且你不关心计算成本，那么考虑添加正则化替代之。

这里有两个额外的策略，重复上一章处理偏差中的方法：

1. 基于错误分析的洞察修改输入特征：假设错误分析启发你去创建额外的特征，以帮助算法消除特定类别的错误。这些新特征可能有助于减少偏差和方差。理论上来说，增加更多的特征可能会增加方差，但如果你发现这种情况，那么就使用正则化方法，它通常能够消除方差的增加。
2. 修改模型架构（如神经网络架构）以便更适合你的问题：这种方法能够影响偏差和方差。

以下是处理偏差和方差问题最简单的方法：

1. 如果具有较高的可避免偏差，那么增加模型的大小（例如，通过添加层/神经元来增加神经网络的大小）。
2. 如果具有较高的方差，那么增加训练数据集。
   如果你可以增加神经网络的大小，并无限制的增加训练集数据，那么可以在很多学习问题上都做的很好。

在实践中，增加网络的模型终将导致你会遇到计算问题，因为训练大的模型很慢。你也可能会耗尽获取更多训练数据的能力。

增加模型的大小通常可以减少偏差，但也可能会增加方差和过拟合的风险。不过可以使用正则化（L2正则化和dropout）来解决（增加正则化一般会增加偏差，但是能减少方差。），这样你通常可以安全的增加模型的大小，而不会过拟合。避免使用更大模型的唯一原因就是计算代价变大。

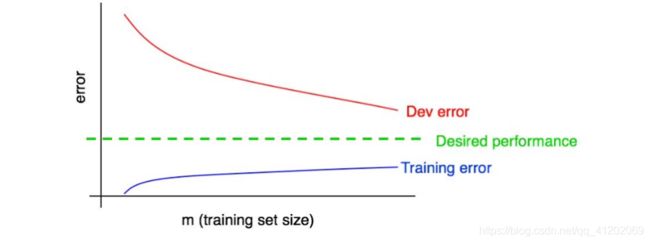
学习曲线

随着训练数据的增加，训练错误和开发错误的波动情况：
两条曲线之间的间隙代表方差，蓝色曲线和绿色横线之间代表偏差

一个标准的“教科书”式的例子（下图，具有高可避免偏差的学习曲线）：在训练集大小的最大处（大概对应我们的所有训练数据），在训练错误和期望性能之间有大的间隙，表明大的可避免偏差。此外，训练和开发曲线之间的间隙小，表明方差小。

参考来源：
参考连接一
参考链接二