Kmeans聚类与dbscan聚类对比

kmeans聚类

特点：
1.无监督学习

2.人为的输入要聚的类数k

3.一般是计算的欧式距离判断相似性

4.每次随机的选取k个聚类中心，聚类结果受随机选取的类中心影响比较大

5.简单

算法过程：

1.输入训练数据集，类别K

2.随机的选取K条数据，作为K个类的中心

3.计算所有数据到2中的K个类中心的距离

4.根据3的结果，与某个类最近的数据化为一类

5.根据4，从新得到K个类，并计算K个类的中心

6.更新上面的的过程，直到K类数据不再变化或者到达迭代次数位置

R语言代码：

n <- 600
x <- cbind(runif(10, 0, 10)+rnorm(n, sd=0.2), runif(10, 0, 10)+rnorm(n,sd=0.2))

km=kmeans(x,5)

km$cluster #输出的聚类标签
km$centers #输出聚类的中心
par(mfrow=c(1,2))
plot(x)
ks=factor(km$cluster)
plot(x)
library(ade4)
s.class(x,fac=ks, add.plot=TRUE, col=rainbow(nlevels(ks)))

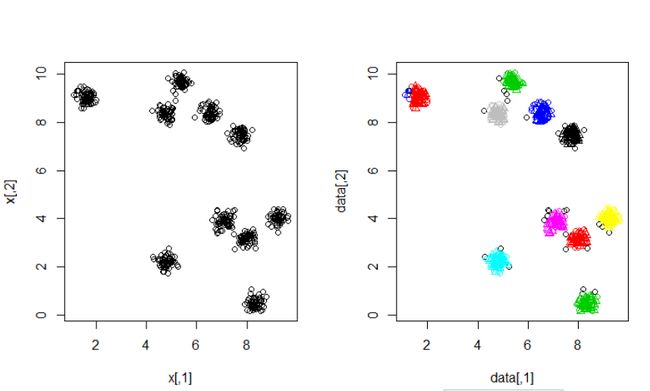
我们选取k=5，第一次运行结果如下：


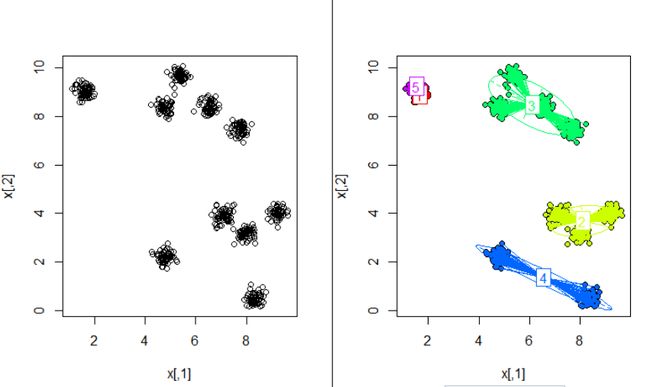
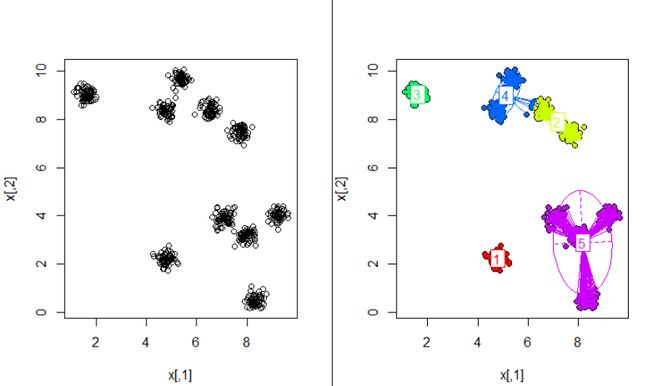
左边的是原始数据的散点图，右边是聚类结果。

由于我们对数据真实聚成多少类无法知道，以及每次都是随机的选取类中心，每次运行的结果可能差不很大。

根据原始数据聚成10类是比较好的。

上面是聚成10类的结果，第二次聚类的结果是我们最想要的。

可以看出，受聚类中心的影响特别大。

当然这个也数据的特性关系很大的，有的数据适合kmeans聚类，有的完全不适合的。

根据上面的数据用dbscan进行聚类

dbscan聚类

dbscan是一种基于密度的聚类算法
与kmeans聚类相比：
1.dbscan可以发现任意形状的数据集
2.且不用输入类别数K

核心是：如果一个点，在距它Eps的范围内有不少于MinPts个点，则该点就是核心点。核心和它Eps范围内的邻居形成一个簇。在一个簇内如果出现多个点都是核心点，则以这些核心点为中心的簇要合并。这样再逐步扩大，形成一个类也就是簇。

dbscan聚类不仅能够发现核心点还能够找到边界点和噪声点，边界点是属于某个类的边界点，噪声点不属于任何一类。

根据上面的数据dbscan聚类代码：

 set.seed(665544)
  n <- 600
  x <- cbind(runif(10, 0, 10)+rnorm(n, sd=0.2), runif(10, 0, 10)+rnorm(n,sd=0.2))
  library(fpc)
  ds <- dbscan(x,eps= 0.2,MinPts=5)
  ds
  plot(x)
  plot(ds, x)

上面程序选取的距离半径eps=0.2，最小点数量MinPts=5
结果如下：

> ds
dbscan Pts=600 MinPts=5 eps=0.2
        0  1  2  3  4  5  6  7  8  9 10 11
border 28  4  4  8  5  3  3  4  3  4  6  4
seed    0 50 53 51 52 51 54 54 54 53 51  1
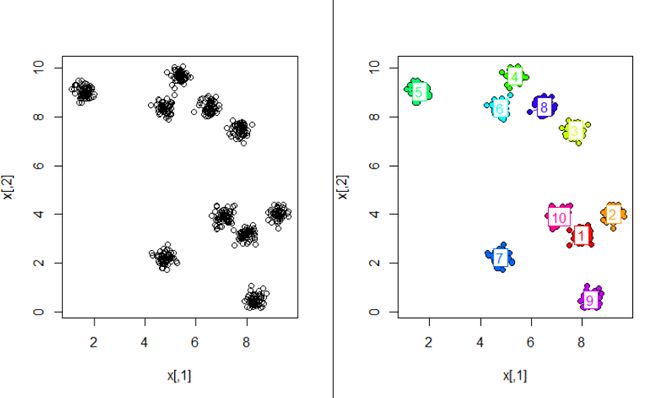
total  28 54 57 59 57 54 57 58 57 57 57  5

多次运行上面程序，结果都一样。
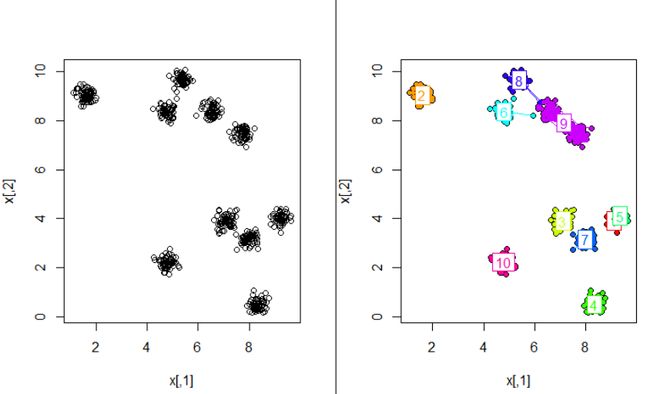
聚成了11类，噪声点28个，最后一类只有一个数据，eps换成0.3，MinPts换成7

> ds
dbscan Pts=600 MinPts=7 eps=0.3
       0  1  2  3  4   5  6  7  8  9
border 3  1  2  2  2   6  2  2  1  3
seed   0 59 57 57 58 114 58 58 58 57
total  3 60 59 59 60 120 60 60 59 60

聚成了9类，噪声点3个，比kmeans结果好多了

出现一个问题，根据输出看到是9类，然而画的图，根据颜色一样是一类就8类，合理的说两个红色的类是两个类。

总结：

不同的聚类适合不同的数据特性

提醒

以后一定要增加Java、Python的代码。