EM,VB,Gibbs Sampling解高斯混合模型

高斯混合模型

假设数据产生过程如下：
$z\sim Mut(\pi )$
$x|z\sim N({\mu }_z,{\sigma }_z^2)$
记$\theta =\{\pi ,{\mu }_1,...,{\mu }_K,{\sigma }_1,...,{\sigma }_K\}$为这个模型的所有参数
观察数据为$D=\{x_i{\}}_N$
采用极大似然估计参数$\theta$
$$log(p(D;\theta ))=\sum _{i=1}^{N}log(p(x_i;\theta ))$$

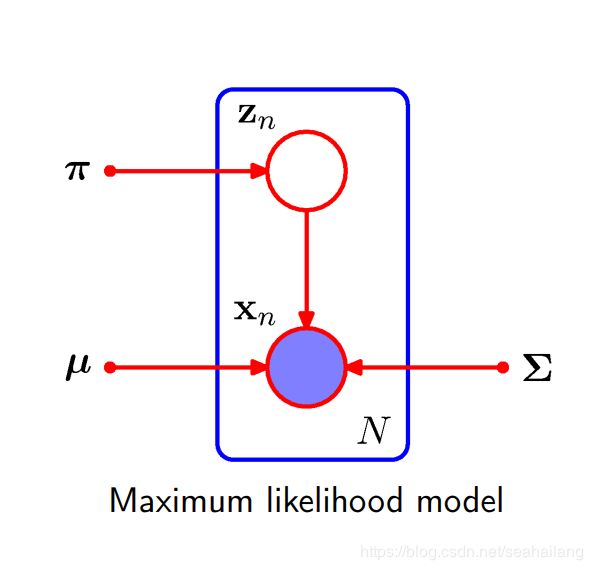
EM算法

直接对上述结果进行优化，由于高斯分布的参数形式比较复杂，并不是那么好计算。
注意到
$$\begin{gathered} log(p(D;\theta ))=\sum _{i=1}^{N}log(p(x_i;\theta )) \\ =\sum _{i=1}^{N}log\left(\sum _{z_i=1}^{K}p(x_i,z_i;\theta )\right) \\ =\sum _{i=1}^{N}log\left(\sum _{z_i=1}^{K}Q(z_i)\frac{p(x_i,z_i;\theta )}{Q(z_i)}\right) \\ \ge \sum _{i=1}^N\sum _{z_i=1}^{K}Q(z_i)log\left(\frac{p(x_i,z_i;\theta )}{Q(z_i)}\right) \end{gathered}$$
最后一步就是Jenssen不等式
注意到，当Jenssen不等式取等号时：
$$\frac{p(x_i,z_i;\theta )}{Q(z_i)}=c\text{ for any zi}$$
只有$Q(z_i)=p(z_i|x_i;\theta )$时，这个式子才是成立的
这样可以采用坐标上升法去求得最优的$Q(z_i)$和$\theta$
E-step:
$$\begin{gathered} \text{固定θ,最优化Q(zi) : } \\ Q(z_i)=p(z_i|x_i;\theta ) \end{gathered}$$
M-step:
$$\begin{gathered} \text{固定Q(zi),最优化θ:} \\ \theta =argma{x}_{\theta }\sum _{i=1}^N\sum _{z_i=1}^{K}Q(z_i)log\left(\frac{p(x_i,z_i;\theta )}{Q(z_i)}\right) \end{gathered}$$
交替进行这两步，即可得到最优的$Q(z_i)$和$\theta$

贝叶斯高斯混合模型

采用极大似然估计不符合贝叶斯学派的一贯作风。我们需要对上述模型加各种先验，使其成为一个贝叶斯模型。
也就是是，对多项分布，我们加上一个共轭的Dirichlet分布作为先验，对于正态分布的，我们加一个共轭的Normal-Wishart 分布作为先验
$\pi \sim \mathcal{D}ir(\alpha )$
$\mathbf{\Lambda }=diag({\sigma }_1^2,...,{\sigma }_k^2)\sim \mathcal{W}(\mathbf{W},\nu )$
$\mu \sim \mathcal{N}({\mu }_0,(\lambda \mathbf{\Lambda }{)}^{-1})$
$z\sim \mathcal{M}ut(\pi )$
$x|z\sim \mathcal{N}({\mu }_z,{\sigma }_z^2)$

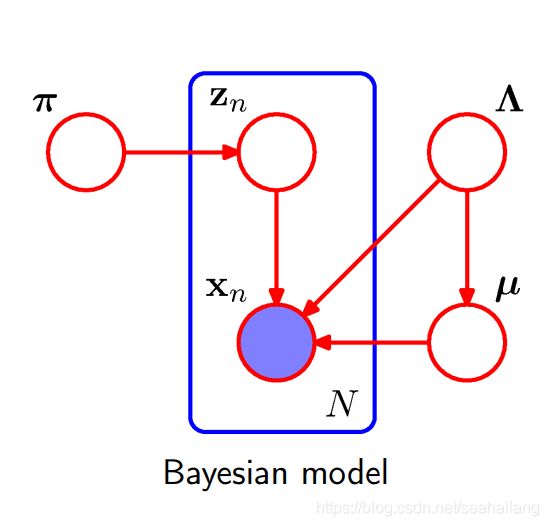
现在将先验参数视为超参数，接下来的过程中，我们认为超参数是固定的
将数据集记为$\mathbf{X}=\{x_i{\}}_N$,所有的隐变量记为$\mathbf{Z}=\{\pi ,\mathbf{\Lambda },\mu ,z_i{\}}_N$
贝叶斯方法就是最大化后验概率
$$p(Z|X)$$
现在我们检查一下我们已知什么，我们已知$p(Z),p(X|Z)$，而
$$p(Z|X)=\frac{p(X|Z)p(Z)}{p(X)}$$
$$p(X)={\int }_{Z}p(X|Z)p(Z)dZ$$
这个积分显然是不易求得的。

变分推断

无法求出$p(Z|X)$,我们换一种思路，求出一个与$p(Z|X)$接近的分布$q(Z)$，以后所有用到$p(Z|X)$的地方，全部用$q(Z)$代替
如何算是接近的分布呢，我们最小化Q和后验的KL距离
$$q^{\ast }(Z)=argma{x}_q{D}_{KL}(q(Z)||p(Z|X))$$
KL距离为
$$\begin{gathered} D_{KL}(q(Z)||p(Z|X) \\ =\int q(Z)log\frac{q(Z)}{p(Z|X)}dZ \\ =-\int q(Z)log\frac{p(Z,X)}{p(X)q(Z)}dZ \\ =\int q(Z)p(X)dZ- \\ \left[\int q(Z)logp(Z,X)dZ-\int q(Z)logq(Z)dZ\right] \\ =p(X)-\left[\int q(Z)logp(Z,X)dZ-\int q(Z)logq(Z)dZ\right] \\ =p(X)-ELOB \end{gathered}$$
由于p(X)是固定的，最小化KL距离，等价于最大化证据下界（evidence low bound）
$$ELOB=\int q(Z)logp(Z,X)dZ-\int q(Z)logq(Z)dZ$$

为了简化处理，我们对自己所用的q(Z)采用平均场假设：
$$q(Z)=\prod _{j=1}^M{q}_j(z_j)$$
那么 $$ELOB=\int ...\int \prod q_j(z_j)logp(Z,X)d{z}_0...d{z}_M-\int ...\int \prod q_j(z_j)\sum logq(z_j)d{z}_0...d{z}_M$$
注意到ELOB实际上是$q_i(z_i)$的泛函

对任意i，
$$ELOB=\int q_i(z_i)E_{j̸=i}[logp(Z,X)]d{z}_i-\int q_i(z_i)log{q}_i(z_i)d{z}_i-\sum _{j̸=i}\int q_j(z_j)log{q}_i(z_j)d{z}_j$$
泛函取极值的条件(欧拉-拉格朗日方程)为
$$\frac{\partial F}{\partial q}-\frac{d}{dz}\frac{\partial F}{\partial q^{\prime }}=0$$
所以对任意i
$$E_{j̸=i}[logp(Z,X)]-log{q}_i(z_i)-const=0$$
得到
$$q_i(z_i)=\frac{1}{C}\exp E_{j̸=i}[logp(Z,X)]$$
这样，变分推断的最优解也可以用坐标上升的方式解决：
依次去i = 1，…,M 固定住其他的j，取得最优的$q_i(z_i)$

VBEM

我们把隐变量处理的更精细写
$\mathcal{Z}=(z_1,...,z_n),\Theta =(\pi ,\mu ,\Lambda )$
$q(Z)=q_z(\mathcal{Z})q_{\theta }(\Theta )$
上述的变分推断可以分成两大部分：
VBE-step:
固定$q_{\theta }(\Theta )$,解最优$q_z(\mathcal{Z})$
$$q_z(\mathcal{Z})=\frac{1}{C_1}exp\left[\int q_{\theta }(\Theta )log(p(\mathcal{Z},\Theta ,X))d\Theta \right]=\frac{1}{C_2}exp\left[\int q_{\theta }(\Theta )log(p(\mathcal{Z},X|\Theta ))d\Theta \right]$$

VBM-step
固定$q_z(\mathcal{Z})$,解最优$q_{\theta }(\Theta )$
$$q_{\theta }(\Theta )=\frac{1}{C}exp\left[\int q_z(\mathcal{Z})log(P(\mathcal{Z},\Theta ,X))d\mathcal{Z}\right]=\frac{1}{C}p(\Theta )exp\left[\int q_z(\mathcal{Z})log(p(\mathcal{Z},X|\Theta ))d\mathcal{Z}\right]$$

需要注意到是这个结果不过是把上一张的结论给重新表达了一下，本质上没有什么不同

变分EM（VEM）

我们比较一下EM和变分推断，发现他们采取的解法都是一样的，固定其他参数，求其中一个参数的最优值。
不同的是EM算法中，最优的$Q(z_i)$就是后验分布，变分推断中最优的$q(Z)$是通过变分法求出来的，EM中关于$\theta$就是一个函数，而变分推断中全部是泛函。
我们的变分推断中还有超参数，一般是假设不变的，但其实也可以在变分推断的过程中使用EM算法
记 $$F(q,\theta )=ELO{B}_{\theta }(q)=\int q(Z)logp(Z,X;\theta )dZ-\int q(Z)logq(Z)dZ$$

VE-step:
固定超参数，计算最优的$q(Z)$
$$q_i(z_i)=\frac{1}{C}\exp E_{j̸=i}[logp(Z,X)]$$
VM-step:
固定$q(Z)$,最优化超参数$\theta$
$${\theta }^{\ast }=argma{x}_{\theta }F(q,\theta )$$

其实我们再给超参数一个先验，VEM算法和变分推断是完全一样的。

Gibss Sampling

注意到我们有两组隐变量 $\mathcal{Z}=(z_1,...,z_n)，\Theta =(\pi ,\mu ,\Lambda )$,
$p(X)=p(X|\mathcal{Z},\mu ,\Lambda )p(\mathcal{Z}|\pi )p(\pi )p(\mu ,\lambda )$
我们想求的是$p(\pi ,\mu ,\lambda |X)$
$$\begin{gathered} p(\pi ,\mu ,\Lambda |X)={\int }_{\mathcal{Z}}p(\pi ,\mu ,\Lambda ,\mathcal{Z}|X)d\mathcal{Z} \\ =\int p(\pi |\mathcal{Z})p(\mu ,\Lambda |\mathcal{Z},X)p(\mathcal{Z}|X)d\mathcal{Z} \end{gathered}$$
我们只要知道P(Z|X),就可以将这个积分算出来
很遗憾，我们没有办法知道。
但是如果我们能够采样出P(Z|X) 的样本，就可以使用蒙特卡洛模拟的方法将这个积分算出来。想要对这个分布采样，我们使用Gibbs 采样，Gibbs采样只需要知道
$$p(z_i|z_{-i},X)\text{ for any i}$$
而
$$p(z_i|z_{-i},X)=\frac{p(z_i,x_i|z_{-i},x_{-i})}{p(x_i|z_{-i},x_{-i})}$$
分母只是一个常数，只关注分子
$$\begin{gathered} p(z_i,x_i|z_{-i},x_{-i})=p(x_i|z_i,x_{-i})p(z_i|z_{-i}) \\ =\int \int p(x_i,\mu ,\Lambda |z_i)d\mu d\Lambda \int p(z_i,\pi |z_{-i})d\pi \\ =\int \int p(x_i|z_i,\mu ,\Lambda )p(\mu ,\Lambda )d\mu d\Lambda \int p(z_i|\pi )p(\pi |z_{-i})d\pi \end{gathered}$$

由于我们采用了共轭的先验，所以上述积分都是可以计算的
前者是个t分布(Gelman et al. [1995] pg. 88)
后者是个多项分布
得到了所有的条件概率后，就可以用Gibbs 采样获得符合分布样本，然后就可以计算出$p(\pi ,\mu ,\Lambda |X)$

VB 与Gibbs的联系

要求$p(Z|X)$
VB的思想是，用$q(Z)={\prod }_i{p}_i(z_i)$来近似。
每次迭代，用变分法求出最优的$q_i(z_i)$
当迭代轮数到一定数量后，就得到了最优的$q(Z)$
Gibss Sampling的思想是
先求$p(z_i|z_{-i},X)$
每次迭代，从上述概率中采样出一个样本出来
当迭代轮数到一个数量后，就采样出了$p(Z|X)$,再用MC的思想进行后续处理。
VB在后验概率部分使用了近似，在得到最优结果时使用的是精确结果
Gibbs Sampling 在后验概率部分使用精确结果，在最后应用时，使用蒙特卡洛的近似

VB每轮迭代，得到的是一个近似的后验分布
Gibbs每轮迭代，是根据准确的后验分布得到一个样本

Ref

https://www-users.cs.york.ac.uk/adrian/Papers/Journals/TSMC-B06.pdf
https://www.doc.ic.ac.uk/~dfg/ProbabilisticInference/IDAPISlides17_18.pdf
https://chrischoy.github.io/research/Expectation-Maximization-and-Variational-Inference/
http://www.robots.ox.ac.uk/~fwood/teaching/C19_hilary_2013_2014/gmm.pdf
https://cse.buffalo.edu/faculty/mbeal/papers/beal03.pdf