图论 —— 最短路 —— Dijkstra 算法

【概述】

Dijkstra 算法是单源最短路径算法，即计算起点只有一个的情况到其他点的最短路径，其无法处理存在负边权的情况。

其时间复杂度是：O(E+VlogV)

【算法分析】

将点分为两类，一类是已确定最短路径的点，称为：白点，一类是未确定最短路径的点，称为：蓝点。

求一个点的最短路径，就是把这个点由蓝点变为白点，从起点到蓝点的最短路径上的中转点在这个时刻只能是白点。

Dijkstra 算法的思想，就是一开始将起点到终点的距离标记为 0，而后进行 n 次循环，每次找出一个到起点距离 dis[u] 最短的点 u ，将它从蓝点变为白点，随后枚举所有白点 Vi，如果以此白点为中转到达蓝点 Vi 的路径 dis[u]+w[u][vi] 更短的话，这将它作为 Vi 的更短路径（此时还不能确定是不是Vi的最短路径）。

以此类推，每找到一个白点，就尝试用它修改其他所有蓝点，中转点先于终点变成白点，故每一个终点一定能被它的最后一个中转点所修改，从而求得最短路径。

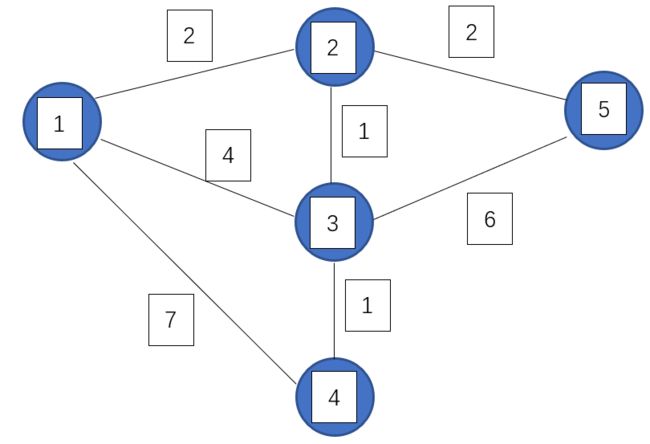
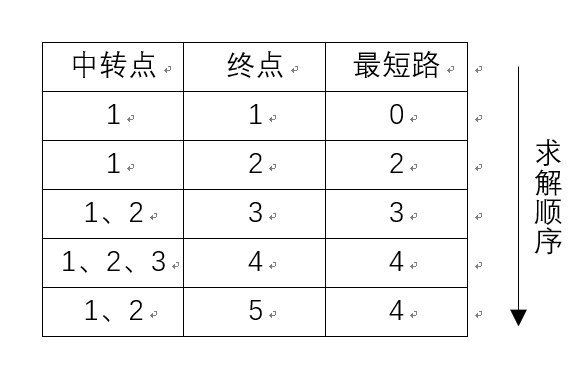
以下图为例

算法开始时，作为起点的 dis[1]=0，其他的点 dis[i]=0x3f3f3f3f

第一轮循环找到 dis[1] 最小，将 1 变为白点，对所有蓝点进行修改，使得：dis[2]=2，dis[3]=4，dis[4]=7

此时，dis[2]、dis[3]、dis[4] 被它的最后一个中转点 1 修改了最短路径。

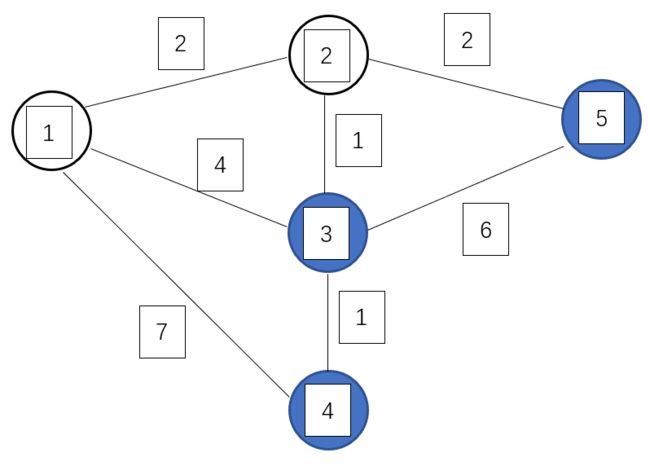
第二轮循环找到 dis[2] 最小，将 2 变成白点，对所有蓝点进行修改，使得：dis[3]=3、dis[5]=4

此时，dis[3]、dis[5] 被它的最后一个中转点 2 修改了最短路径。

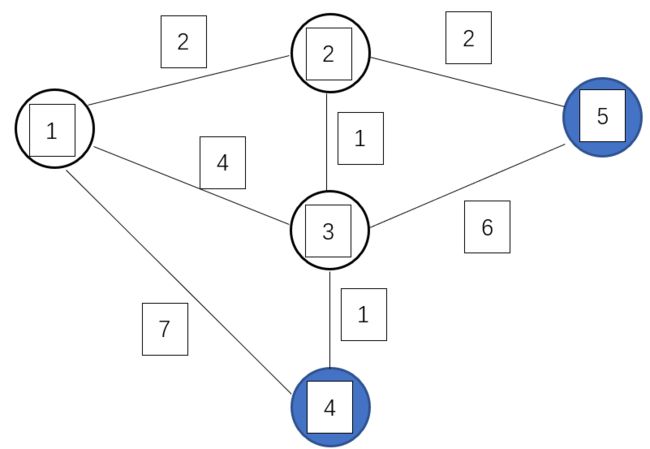
第三轮循环找到 dis[3] 最小，将 3 变成白点，对所有蓝点进行修改，使得：dis[4]=4。

此时，dis[4] 被它的最后一个中转点 3 修改了最短路径，但发现以 3 为中转不能修改 5，说明 3 不是 5 的最后一个中转点。

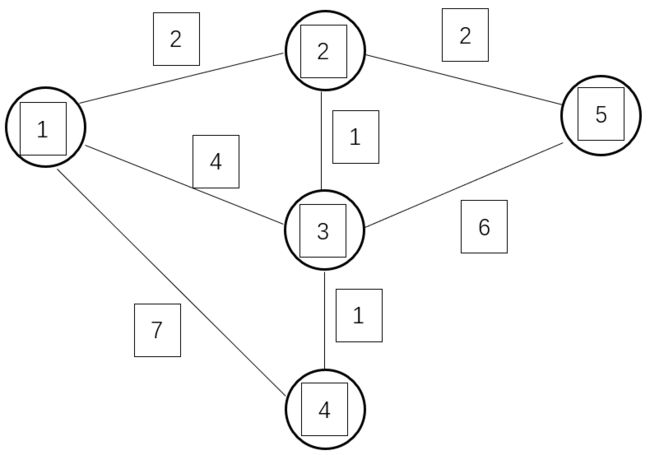
接下来两轮循环将 4、5 也变成白点。

N轮循环结束，所有点的最短路径均可求出。

【算法描述】

设起点为 s，dis[v] 表示从 s 到 v 的最短路径，pre[v] 为 v 的前驱结点，vis[v] 用于记录 v 是否被访问过。

1.初始化：

dis[v]=0x3f3f3f3f（v≠s），vis[v]=false，即：从始点到各点的值初始化为一极大值，所有点均标记为未访问

dis[s]=0，pre[s]=0，即：始点到始点的距离为 0，且其没有前驱结点

2.算法主体：

for(int i=1;i<=n;i++) {
    int min=INF;
    int u=0;
    
    for(int v=1;v<=n;v++) { //在没有被访问过的点中找一个顶点u，使得dis[u]是最小的
        if( vis[v]==false && dis[v]

3.算法结束：

dis[v] 即为 s 到 v 最短距离，pre[v] 即为 v 的前驱结点，用来输出路径。

【模版】

1.简化版

简化版不可处理重边图

int n;//图节点数目,从1到n编号
int dis[N];//单源最短距离
int G[N][N];//G[i][j]表示i到j的有向边长
bool vis[N];//表示w[i]是否已经计算完
void dijkstra(int s){
    for(int i=1;i<=n;i++){
        int x;//x标记当前最短w的点
        int min_dis=INF;//记录当前最小距离
 
        for(int y=1;y<=n;y++){
            if(!vis[y] && min_dis>=dis[y]){
                x=y;
                min_dis=dis[x];
            }
        }

        vis[x]=true;
 
        for(int y=1;y<=n;y++) 
            dis[y]=min(dis[y],dis[x]+G[x][y]);
    }
}
int main(){
    memset(dis,INF,sizeof(dis));
    memset(vis,0,sizeof(vis));

    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){
        int x,y,dis;
        scanf("%d%d%d",&x,&y,&dis);
        G[x][y] = G[y][x] = dis; //无向图添边一次,有向图添边两次
    }
    int start;
    scanf("%d",&start);
    dijkstra(start);
    for(int i=1;i<=n;i++)
        printf("%d\n",dis[i]);
    return 0;
}

2.标准版

标准版适用于稀疏图，可处理重边图

int n,m;
struct Edge{//边
    int from;//边的起点
    int to;//边的终点
    int dis;//边的长度
    Edge(int f,int t,int d){//构造函数
        from=f;
        to=t;
        dis=d;
    }
};

struct HeapNode{//Dijkstra用到的优先队列的结点
    int dis;//点到起点距离
    int u;//点的序号
    HeapNode(int a,int b){
        dis=a;
        u=b;
    }
    bool operator < (const HeapNode &rhs) const  {
        return dis > rhs.dis;
    }
};

struct Dijkstra{
    int n,m;//点数、边数
    vector edges;//边列表
    vector G[N];//每个结点出发的边的编号
    bool vis[N];//是否走过
    int dis[N];//起点s到各点的距离
    int p[N];//从起点s到i的最短路中的最后一条边的编号

    void init(int n) {//初始化
        this->n = n;
        for(int i=0;i Q;//优先队列
        Q.push(HeapNode(0,s));
        while(!Q.empty()) {
            HeapNode x=Q.top();
            Q.pop();

            int u=x.u;
            if(vis[u])//若已被访问
                continue;

            vis[u]=true;//标记为已访问
            for(int i=0;i dis[u]+e.dis) {//更新距离
                    dis[e.to] = dis[u]+e.dis;
                    p[e.to]=G[u][i];
                    Q.push(HeapNode(dis[e.to],e.to));
                }
            }
        }
        return dis[n];//返回起点s到终点n最短距离
    }
}DJ;

int main()
{
    while(scanf("%d%d",&n,&m)!=EOF&&(n+m))
    {
        DJ.init(n);//初始化
        for(int i=0;i%d: %d\n",s,++j,DJ.dis[i]);
    }
    return 0;
}