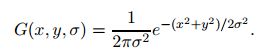对SIFT算法的理解，尤其是尺度不变性
SIFT算法四大块
1，尺度空间的建立，最难理解的部分，这一步是为了找到极值点的潜在位置
2，极值点精确定位，通过曲线拟合找到极值点的确切位置
3，分配主方向，为特征点赋予一个方向标志，固定生成描述子所用到的领域信息
4，生成描述子，用特征点周围的像素的梯度刻画这个描述子，用梯度描述是可以增强鲁棒性的
匹配的时候，同一个特征点得到的描述子相差无几，因为它们是由特征点周围相同的图像信息得到的。
SIFT invariant to scale and rotation， robustness to
1. affine(rotation scale shear) distortion
2. change in 3D viewpoint
3. addition of noise
4. change in illumination
优点：
Locality：特征点是局部的，可以对抗遮挡和背景干扰（occlusion and clutter）
Distinctiveness：单个特征可以匹配一个数据集
Quantity：小物体也能产生大量特征点
怎样做到尺度不变性
SIFT的全称是Scale-Invariant Feature Transform，这就表示尺度不变性是这个算法最精髓的地方。怎样理解尺度和尺度不变性呢？
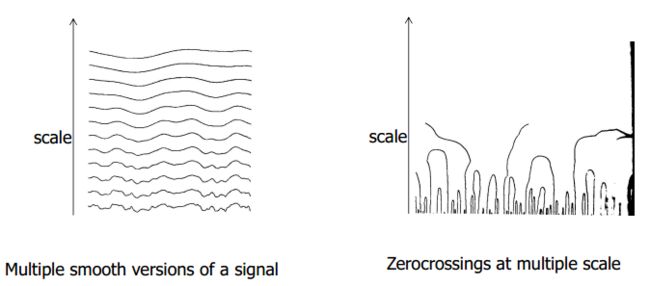
什么是尺度，很多人会从视觉的角度去理解，这是一种直观的理解方式，可以帮助我们理解，但是怎样才能做到这种视觉效应呢，上世纪八九十年代很多学者做了了不起的研究。图像的边缘点是我们感兴趣的点，边缘检测的方法有很多，当我们用Canny，LoG检测边缘点时候，sigma值代表着什么，当我们用不同的sigma得到很多边缘图像，这些边缘图像之间又有什么联系?Marr和Hildreth在1980年提出Spatial Coincidence assumption：在不同的scale下都能检测到的过零点具有物理意义。1983年，Wiktin将所有Guassian scale都作用到信号上，提出尺度空间的概念，观察过零点和尺度空间的关系，以一维信号为例：
可以看出，scale变大的时候信号越来越平滑，最后过零点消失，更进一步，过零点的轮廓在底部张开，慢慢合并并消失，呈现一个拱形。
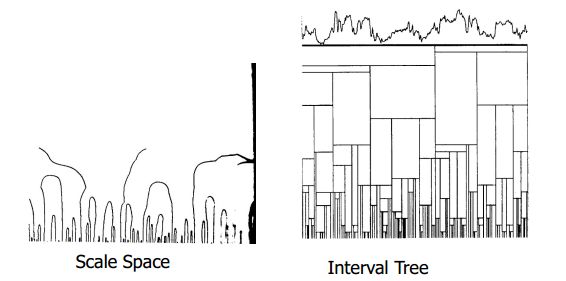
将过零点图画成Interval Tree再进一步分析（横坐标是Interval）：
Parent结点的Interval更大，off springs的Interval更小，从上往下是不断分裂的，结点存在的scale范围可以看作这个结点的稳定性，描述这个过零点的时候：如果一个结点比它的上下两个结点都不稳定，就要从Interval Tree上去掉。
下面直观的看一系列不同scale的LoG作用在图像上一个角点会出现什么情况：
随着作用的scale增大，这一点的灰度值都出现了一个峰值。这就是尺度函数的精华所在，我们称之为scale signature。虽然这两张图初始尺度不一样，但是它们都在某个scale下出现了极值。那么被不同scale 的 LoG选出来的点有什么特性呢？
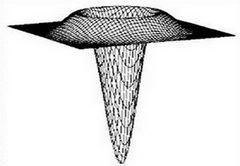
LoG长这个样子：
中间凸起的区域真是被LoG选中起作用的点，当scale变化时，被选中的范围是这么变的：
LoG实际上是检测一个块状区域，我们姑且这么描述：以一个点为半径，画一个框，这个框由小变大可以框出这点周围的图像信息，这些信息在某个大小的框下按照某个规则线性组合后可以达到最大值或最小值。这个特性应用到尺度上就是你对着同一个物体拍一张图，对于一些点，不管你图片初始尺寸是多少，我都能调整LoG的半径使这个点在作用后达到级值，在达到极值的尺度下所框出的信息量是一样的。举个例子，有一条边缘曲线，全局看过去的时候是这样的：
我们用不同的圈去框那个角点，也就是不同尺度作用在图像上，在红色框时灰度值达到最大值。现在我们将图像放大，继续用不同的圈去框那个角点：
这样在红色大框下达到最大值，最重要的一点是：这两个框框出来的图像信息其实是一样的，只是原图尺寸不一样，导致达到极值时需要的框不一样大！
比如说一张美女图片，想要框出帽子的信息，图像尺寸小时框要这么大：
图像尺寸大时，框也要相应调大：
不管原图尺度是多少，在包含了所有尺度的尺度空间下都能找到那些稳定的极值点，这样就做到了尺度不变！接下来的问题就是建立尺度空间的函数要怎么选呢？Koenderink(1984)和Lindeberg(1994)证明了在一些假设下，高斯函数是唯一可行的尺度空间核：
Lindeberg(1994)证明尺度归一化的LOG是保证尺度不变所必须的（scale-normalized Laplacian of Gaussian, σ2∇2G）。Mikolajczyk(2002)在实验对比中证实相对于Gradient，Hessian，Harris corner function，σ2∇2G得到的极值是最稳定的。因此，选用LoG构建尺度空间，但是LoG计算太复杂了。Lindeberg(1994)发现由热传导方程，将t换成sigma：
而
联立得到：
和尺度归一化的LoG只相差一个倍数k-1，这个倍数是一个常数，不影响极值点检测。
因此我们就可以用DoG近似LoG，具体做法就是将相邻两层的高斯尺度图像相减：
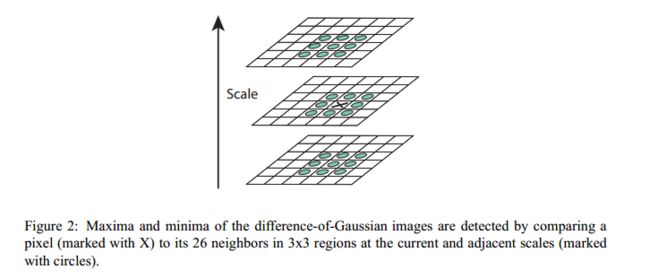
得到DoG以后每一个点都和本层及相邻两层的3*3领域26个点比较，是极值则被选中，是潜在的特征点：
理论上我们需要连续的尺度空间，但是是做不到的，scale该取哪些值，也就是初始尺度要取多少，k要取多少？在SIFT中，Lowe教授还利用了降采样来减少计算量，尺度空间形成了类似金字塔的结构，相同尺寸的图片属于一组（Octave），每一组单张图片叫做一层（Scale），并且，Lowe将原图升2插值作为第0组。整体结构变成了这样：
为了在每组中检测S个尺度的极值点，DOG金字塔每组需S+2层图像，因为DOG金字塔的每一层和其上下两层比较得到极值点，第一层和最后一层是不能检测极值点的，而DOG金字塔由高斯金字塔相邻两层相减得到，则高斯金字塔每组需S+3层图像。
首先谈谈层数的确定：
Lowe做了两组实验，将同一张图片进行不同的变换，统计不同层数下特征点被检测到的重复率，这些特征点在数据集中的匹配成功率；不同层数下检测到的特征点数量，得到：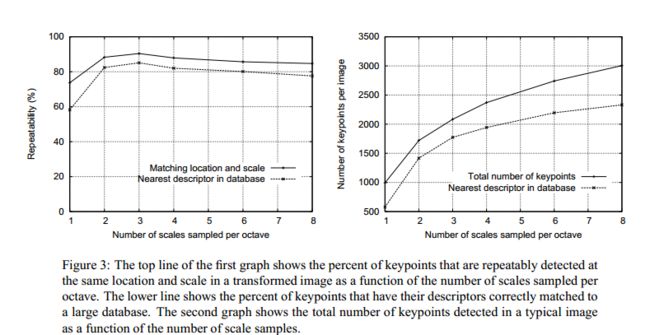
经过折中，层数（用S表示）选择3。这个层数指的是可以检测极值点的层数，并且将尺度的采样间隔设为2^(1/S)。
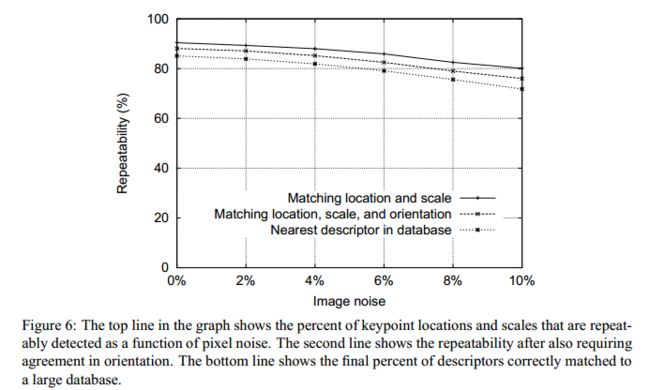
再谈谈初始尺度sigma0的设定：
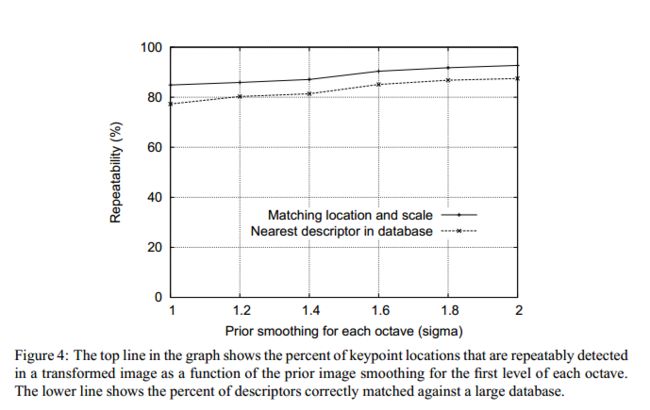
同样经过试验，统计不同初始尺度下，特征点检测重复率以及在数据集中的匹配成功率，得到：
确定sigma0=1.6.另外Lowe假设图片经过相机拍摄后具有了0.5的尺度（原文：We assume that the original image has a blur of at leastσ= 0.5(the minimum needed to prevent significant aliasing) ），经过双线性插值扩大一倍后的第0组第0层图像尺寸就为1。至于为什么要扩大图像，Lowe的解释是：The image doubling increases the number of stable keypoints by almost a factor of 4, but no significant further improvements were found with a larger expansion factor. 可以理解为在检测极值点前对原始图像高斯平滑会丢失高频信息，所以 在建立尺度空间前首先对原始图像长宽扩展一倍，以保留原始图像信息，增加特征点数量。
最后谈谈组数的确定：
M,N是原始图像的大小。这个3其实是金字塔顶层图像长、宽的最小值的对数，但由于图像尺寸太小信息就丢失严重，所以太小了也没意义，就将顶层最小尺寸定位8×8，可以调整。
最终，SIFT构建了如下的尺度空间，这里指的是高斯金字塔：
每一组，初始尺度sigma，各层尺度k倍关系
，S为检测极值点的层数。
第0组第1层的尺度设为1.6，S取3，
，高斯金字塔有S+3=6层，这样各个层尺度就都有了。高斯平滑具有一个平方特性，即进行一次
的平滑，再进行一次
的平滑，相当于进行一次
的平滑。
第0组第0层由原图插值得到，尺寸为1，第1层由第0层平滑得到，由平方关系，第一层的高斯平滑尺度应为：
。则第s层用的高斯平滑尺度应为：
。
而下一组的第1层图像是由上一组的倒数第三层降2采样得到的。到次，每一组每一层的尺度就都确定了：
。
Lowe选用的尺度空间构成如下图：
那为什么下一组的第一层图片要用上一组的倒数第三层采样呢？
上一组的初始尺度为
，上一组倒数第三层的尺度为
，也就是下一组的第一层尺度，在得到DoG后中间的层数被选出来检测极值点，上一组是
，下一组是
，而
，刚好和
连续起来，
，这样就构造了连续的尺度空间！参看上图红色的检测极值点用的尺度。
至此，尺度不变性完成，不管你原图怎么缩放，都能够找到相同的极值点。
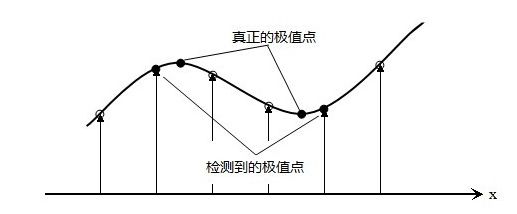
后话，由于这里的尺度离散化了，图像的灰度坐标也是离散化的，求得极值点后Lowe将DoG空间进行曲线拟合再插值找到精确的极值点位置。
怎样做到旋转不变性
由上面的分析我们得到特征点所在尺度是和原图尺寸紧密相关的，在实际应用中，我们不仅会接触到不同尺寸的图片，而且这些图片还可能经过了不同的旋转。怎样克服图片的旋转呢？就是要保证在生成描述子时要用的是同一块图像信息，4×4的框也要框出的是同一块信息！Lowe采用的方法是在生成描述子前将图片旋转到一个特定的方向上，这个方向是根据图片内容得到的，具体就是用在某个半径大小的圆内的像素的梯度信息。保证一个特征点生成描述子用的是同一块信息，就是由于生成主方向用的梯度直方图用的sigma取的是1.5*
这样就能保证坐标轴和图像的相对位置保持一致。
怎样达到一定的仿射不变性
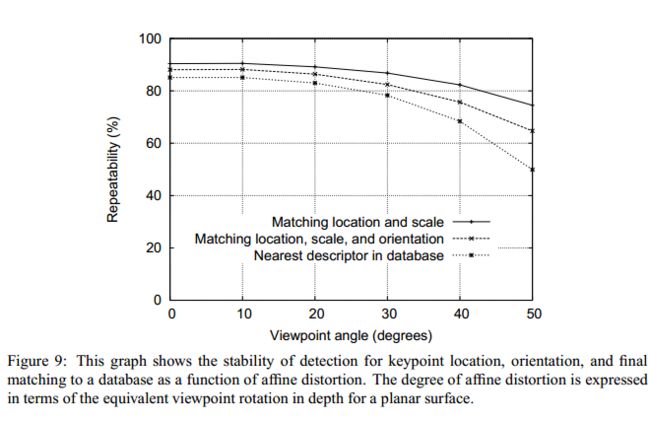
用梯度信息生成描述子，由于梯度的稳定性，这本身就具备了一定的抵抗仿射的能力。另外生成梯度直方图时都用了高斯加权，距离特征点近的梯度幅值有较大权重，弥补了没有考虑仿射不变性带来的特征点不稳定。抵抗仿射的能力如下：
怎样做到光照不变性
描述子生成采用梯度是有理论依据的（待学习），生成描述子用领域像素的梯度直方图，可以增强算法的鲁棒性，可以抵抗光照变化，仿射，3D 旋转（Edelman, Intrator, and Poggio(1997)），并且允许特征点的位置在小范围内shift。图像的梯度是相邻像素点相减得到的，可以增强灰度不变性，避免因图像整体灰度漂移造成的不稳定。
怎样抵抗噪声
在DoG得到极值点后，去除低对比度的点
的点舍弃，可以抗噪，因为这些点灰度值小，容易受到噪声的影响而变得不稳定，或者本身就是噪声。
模仿Harris角点检测，用Hessian矩阵去掉强的边缘响应点，DOG has strong response along edge，所以会检测出很多边缘点，而这些边缘点并一定都是稳定的极值点。
在确定主方向和生成描述子时都将梯度模值加进行加权，即是噪声影响了部分点，经过加权统计会抑制变化，不会对全局造成太大影响。
Lowe教授经过试验，得出抗噪性能如下：
SIFT的matlab实现可以在此下载：SIFT算法的matlab实现