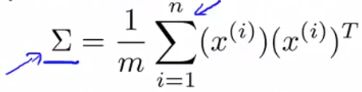吴恩达《Machine Learning》-Dimensionality Reduction降维（十四）

Data Compression数据压缩

为了让机器学习算法的运行效率更高，我们一般对于一些有特点的数据采取数据压缩。
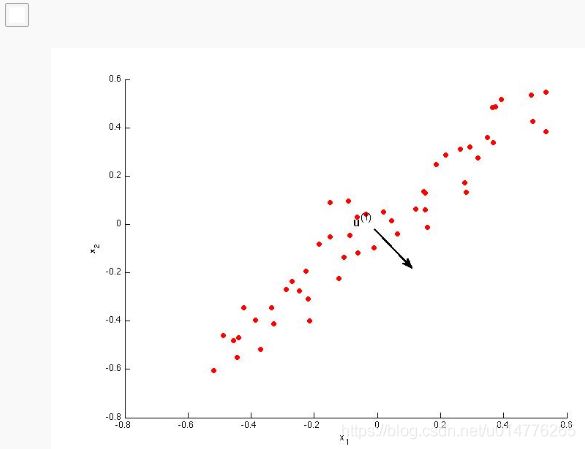
如上图，数据集大多分布在一条线上附近，这种数据我们可以采用数据压缩。其操作是将直线附近的数据投影在本直线上。相当于将一个二维数据，降维成一维数据。

同理多于三维数据，我们也可以考虑投影在二维平面。（一般三维数据分布在二维平面附近）。此时我们仅仅需要两个维度，即投影二维平面的Z1轴与Z2轴来表示数据。

练习题：

选择（C）
C.一个低维的数据集（但是数据集应该包含所有的数据，故其数量为m个），但是降低维度的特征数量应该小于或等于现有的特征数量

Visualization可视化

假如我们现在有一个50维的数据集，所以当前特征数一般为50

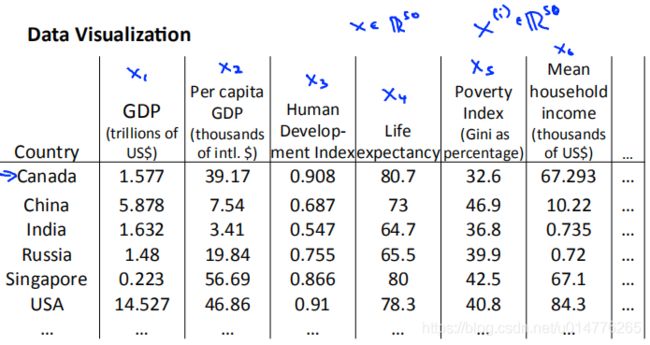
但是为了可视化数据，一般需要我们压缩数据入二维或者三维。因为人眼只能看到二维或者三维。

压缩到二维数据，然后画出图像。

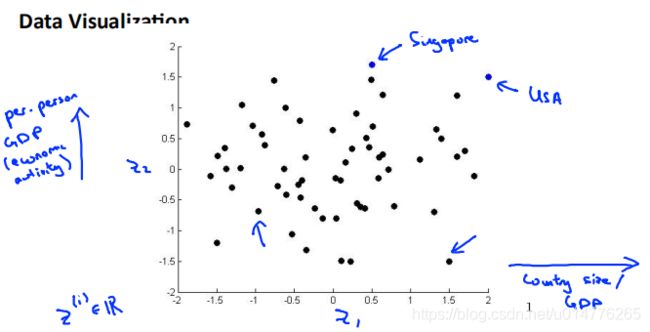
练习题：

选择（B，D）
D.我们只能画出2D或者3D图像，因为我们人无法可视化出超过三维的图像

Principal Component Analysis Problem Formulation主成分分析问题公式

使用PCA之前我们需要使用标准化（feature scaling），均值归一化（mean normalization），这样特征x1和x2的平均值应该为零。


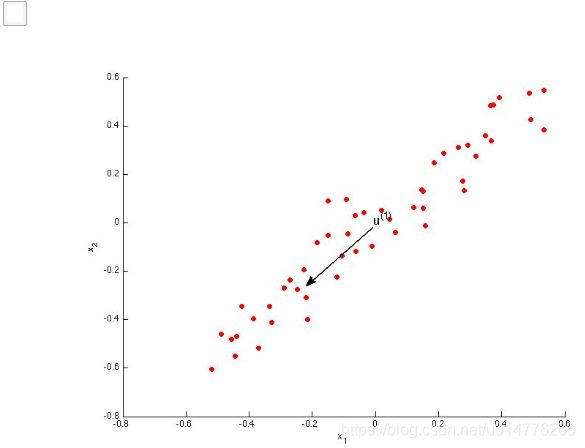
使用PCA算法将数据点投影在最近拟合的一条直线上。其中数据点与直线之间的距离，叫做投影误差（projection errors）我们需要最小化投影误差，使数据点与投影直线之间的距离达到最小。

而如果讲数据点投影到粉色线段上，其距离是很大的，故如果投影到粉色线段上其投影误差也是巨大的。这就是为什么主成分分析PCA会选择像红线这样的东西，而不是下面的粉色线。

对于减少二维到一维，我们如何找到那条投影误差最小的直线。
在这个例子中，我希望PCA能找到这个向量，我想称之为u（1），这样当我把数据投影到我定义的线上，我最终得到了很小的重建误差。
对于n维的特征，我们需要找到k维的向量，来作为我们的用来投影的东西（如，用来投影的直线，平面，等等）。其k维向量，最后投影出来的投影误差应该是最小的。

PCA与线性回归的区别

左图为线性回归，右图为PCA。
线性回归一般为y方向上的距离，PCA一般采用垂直于线段的投影距离。
另外对于数据来说，PCA没有数据的标记值。线性回归为(x1,x2,x3,y)，y为标记好的分类值。

练习题：

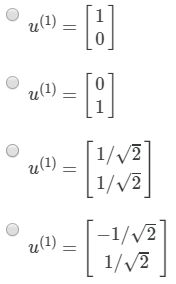
选择（D）
D.这条直线应该是2，4象限角平分线。故其向量为D，且这条向量的模为1.其平方和再开根号的值，应为1.

主成分分析算法

我们的目标是计算直线向量u⁽¹⁾和数据集点投影在直线上的z⁽ⁱ⁾

第一步是均值归一化。我们需要计算出所有特征的均值，然后令 ?? = ?? − ??。如果特

征是在不同的数量级上，我们还需要将其除以标准差 ? 2。

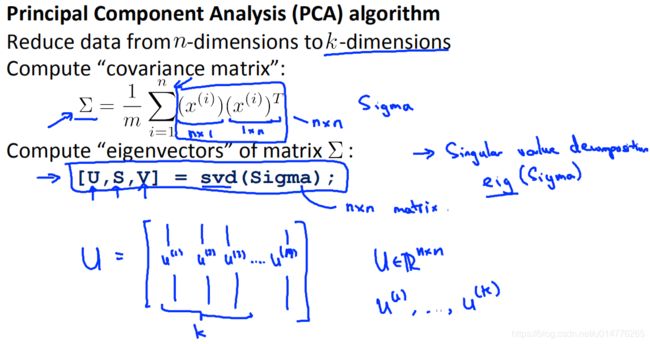
##### 第二步是计算协方差矩阵（covariance matrix）：

第三步是计算协方差矩阵?的特征向量（eigenvectors）:

在 Octave 里我们可以利用奇异值分解（singular value decomposition）来求解，[U, S,

V]= svd(sigma)。

原因：

svd函数与eig函数是两个不同的计算函数。但是在本例中，使用svd函数与eig函数计算出来的结果都是一样的。（即，这两个函数拥有相同的效用）因为，协方差矩阵（covariance matrix）总是满足一个称为对称正定（symmetric positive definite）的数学性质。所以其计算结果与计算特征向量的结果一样。而一般情况下，我们会采用eig函数，计算特征向量（eigenvectors）。

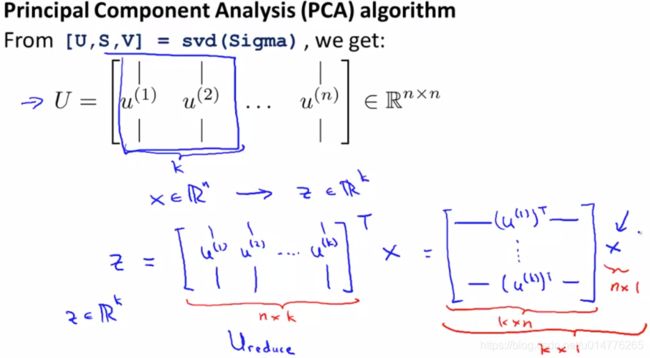
如果我们希望将数据从?维降至?维，我们只需要从?中选取前?个向量，获
得一个? × ?维度的矩阵，我们用???表示，然后通过如下计算获得要求的新特征向量? (?)
z的维度求法如下：
Ureduce为n × k的矩阵，Ureduce的转置为k × n的矩阵，x为n × 1的矩阵，所以z为k × 1的矩阵

向量表示法与数值表示法

练习题：

选择（D）
zj表示第j个z向量的值，故应采用第j个矩阵（u^(j)）^T乘上全量的数据集x

Reconstruction from Compressed Representation重建压缩

在以前的视频中，我谈论 PCA 作为压缩算法。在那里你可能需要把 1000 维的数据压缩100 维特征，或具有三维数据压缩到一二维表示。所以，如果这是一个压缩算法，应该能回到这个压缩表示，回到你原有的高维数据的一种近似。
所以，给定的?^(?)， 100 维，怎么回到你原来的表示?
^(?)，是 1000 维的数组？

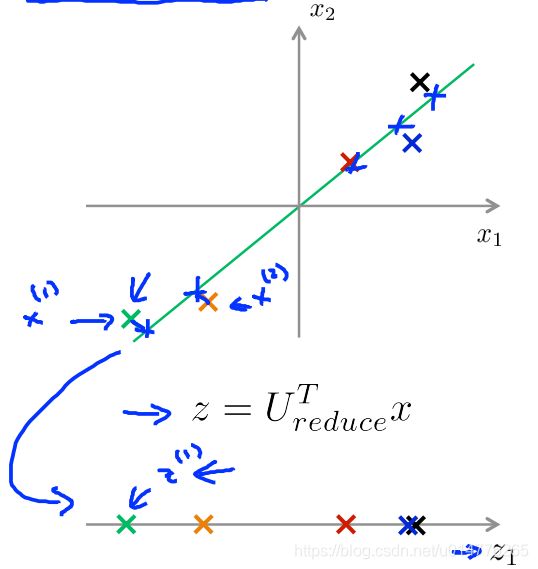
解决的问题是，如何将z转化回x。

Xapprox的维度求法如下：

Ureduce为n × k的矩阵，z⁽¹⁾为k × 1的矩阵(即直线上第一个点为z⁽¹⁾)，所以Xapprox⁽¹⁾为n × 1的矩阵


选择（A，B，C）
Ureduce为 n × n的矩阵，Ureduce的转置为 n × n的矩阵，x为n × 1的矩阵
B.Xapprox ​= 数据集中每个x。
C.k=n故其方差一样

Choosing the Number of Principal Components选择主要成分的数量

K是PCA算法中的参数。我们下面讨论如何选择PCA算法的参数，K。这个数字k也被称为主成分的数量或者我们保留的主成分的数量。

使用均方投影误差（Average squared projection error），代表数据集投影在直线上的垂直距离，除上 数据集的变化（Total variation in the data）。小于等于0.01（1%），代表保留99%的差异。

左边为传统算法，计算出k值。右边为简易算法。
左边算法，尝试k从1，2，3…，检查哪一个k符合
公式的要求。
右边算法，尝试加和对角线上元素。分子是从1到k开始加和，分母是从1到n开始加和。

简化原因：

因为这给了你s矩阵，一旦你有了s矩阵，你就可以通过增加分子中k的值来继续计算，这样你就不需要反复调用svd来测试k的不同值了。所以这个过程更有效。很好，这可以让你选择k的值，而不需要从头开始运行PCA。

将1-∑Sii/∑Sii ≤0.01 转化为 ∑Sii/∑Sii ≥0.99 更为直观。99%显示了投影之前与原数据集相似度为99%

练习题：

选择（C）
投影平方误差 (squared) projection error，公式如选项C所示。

实施PCA的建议Advice for Applying PCA

将数据集中的x提取出来，形成x⁽¹⁾，x⁽²⁾，…，x^(m)。然后使用PCA算法，将x降维，形成z，即z⁽¹⁾，z⁽²⁾，…，z^(m)。这样就形成了新的训练集（z⁽¹⁾，y⁽¹⁾），（z⁽²⁾，y⁽²⁾）…
使用PCA算法训练出的结果为Ureduce。不同的训练集训练出不同的结果，其Ureduce也不同。

PCA的应用

（1）数据压缩

用途：

减少存储空间
加速机器学习算法运行

核心思想：

其主要是选择合适的k，来让k保留更多的细节

（2）可视化

核心思想：

k=2或k=3，来得到二维或三维数据图像

错误使用PCA的案例：

使用PCA来避免过拟合是错误的。因为PCA中仅仅使用到了x数值，对于数据值的标记值y没有使用。也就是说，使用PCA将会丢掉一部分信息，即数据会产生损失。但是采用正则化来解决过拟合问题更合适，因为其公式了加入了标记值y，不会丢掉信息。

建议先使用原数据集运行PCA，如果原数据集上运行算法其运行速度慢且占用大量磁盘空间。后再考虑使用PCA算法。

练习题：

选择（A，B，D）
A.PCA能够压缩存储空间
B.PCA能够减少输入的训练数据，来加速机器学习算法运行
D.PCA能够将高维数据可视化

测试题：

选择（A，B）

选择（B）
B.选择最小值的k，其至少保留99%的方差的

选择（B）
B.小于等于0.05即拥有95%的variance was retained

选择（B，C）
B.使用PCA之前实行标准化
C.给定一个输入矩阵x，PCA算法能压缩其进入一个低维的z矩阵

选择（B，D）
B.PCA能够减少输入数据集的维度
D.PCA能够减少磁盘存储空间