《算法基础》——3.8 循环链表

本节书摘来自华章计算机《算法基础》一书中的第3章，第3.8节，作者：（美）罗德·斯蒂芬斯（Rod Stephens）著，更多章节内容可以访问云栖社区“华章计算机”公众号查看

3.8　循环链表

循环链表指一个最后的链接指回链表中第一个项的环形链表。图3-9显示了一个循环链表：
当需要链表的项按照顺序无限循环时，循环链表是有用的。例如，操作系统可能会通过反复地循环一个进程链表，给每个进程执行的机会。如果一个新的进程启动时，它可以在任何地方添加到进程链表中，可能就在当前进程后，这样它就可以马上获得一个被执行的机会。
再举一个例子，一个让某链表无限循环的游戏，允许每个项移动至屏幕上。因此，新的对象，可以随时随地被添加到链表中。
图3-10显示了一个包含循环的链表，但循环不包括链表中的所有单元格：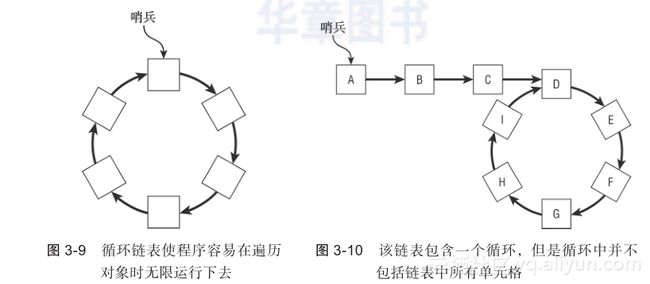

在图3-10所示的这种链表中有趣之处在于它提出了两个有意思的问题。首先，怎么能发现一个链表是否包含这样一个循环？其次，如果链表中包含这样一个循环，怎么找到这循环的开始，并破坏它来进入循环链表？这和问链表的底部单元格在哪儿是大致相同的问题。在图3-10中，可以定义链表的底部单元格为I，因为它是开始重复遍历链表前的最后一个单元格。以下各节描述了一些很有趣的算法，来回答这些问题。
3.8.1　标记单元格
也许判断一个链表有一个循环的最简单方法是，访问每个单元格的同时做一个标记。如果来到一个已经被标记的单元格，就知道链表有一个循环，并且循环从这一单元格上开始。下面的伪代码显示了这个算法：

该Has_loopMarking示例程序演示了这一个算法，友情提示：它可以从这本书的网站上下载。
该算法需要遍历链表两次，一次将单元格的访问标记设置为true，第二次将它们重新设置为false。因此，如果该链表包含N个单元格，该算法需要2×N个步骤，运行时间为O(N)。该算法还要求每个单元格有一个额外的访问字段，所以它需要O(N)的空间。这个链表已经占据了O(N)的空间来容纳单元格和它们之间的链接，所以这不应该是一个问题，但不得不承认，该算法具有一定的内存需求。
注　标记单元格是一种简单的技巧，对于其他的数据结构，尤其是网络都适用。在第13章和14章中我们将提到一些使用了标记技巧的算法。
在某些问题中常常有这么一个额外的要求：不能更改单元格类型的定义。在这种情况下，这意味着不能添加一个访问字段。下节介绍的算法则满足了这一种额外的限制。
3.8.2　使用散列表
散列表在第8章中将会详细的描述。现在，只需要知道一个散列表能快速地存储一个项、检索项并且分辨某一项在散列表中是否存在。
该算法沿着链表移动，将每个单元格存放进散列表中。当访问一个单元格，它会检查散列表，看是否该单元格已在表中。如果发现一个单元格已经在散列表中，这证明该链表包含一个循环并且从该单元格开始。
下面的伪代码展示了这一算法：

该HasLoopHashTable示例程序演示了这一算法，友情提示：它可以从这本书的网站上下载。
该算法遍历链表中的单元格一次，因此，如果该链表包含N个单元格，该算法需要O(N)的时间来运行。
该算法还需要一个散列表。为了获得最佳性能，散列表的空间必须比它将存放的值所占空间更大。所以对于这个算法，散列表必须有足够的空间存放比N多的项。一个拥有1.5×N个项的散列表将提供良好的性能，并仍然使用O(N)的空间。
该算法遵循不允许修改单元格类型的限制，但使用额外的存储空间。以下各节描述了一些算法来检测环路，而无需使用额外的存储空间。
3.8.3　链表回溯
链表回溯算法使一个对象遍历链表。对于每个已经访问过的单元格，该算法使第二个对象遍历链表，直到它找到第一个对象。如果两个对象之前的单元格是不同的，则该链表中包含了循环。
这种描述似乎有点混乱，但看完下面的伪代码后，算法应该能够理解：

该HasLoopRetracing示例程序演示了这一算法，友情提示：它可以从这本书的网站上下载。
假定该链表包含N个单元格。当算法的cell对象在检查链表中的第K个单元格时，tracer对象必须遍历该链表到这一单元格，因此它必须执行K步。这意味着该算法的总运行时间为1＋2＋3＋…＋N＝N×(N＋1)÷2＝O(N2)。这是比以前的算法慢，但是，和之前的算法不同，它不需要额外的空间。
下一个算法不仅仅不需要额外的空间，而且它仅需要运行O(N)的时间。
3.8.4　反转链表
反转链表算法遍历链表，扭转每个单元格的链接，使其指向该单元格之前的单元格而不是它之后的单元格。如果算法到达链表中的哨兵单元格，则链表中包含一个循环。如果该算法到达一个空链接而没有到达哨兵单元格，则链表中不包含循环。
当然，将链接扭转会弄乱链表。如果要恢复链表，算法则要再一次从链表后面往前面遍历，再次扭转链接，使它们指向的地方回复到最初的状况。
要了解其工作原理，请看如图3-11所示的链表：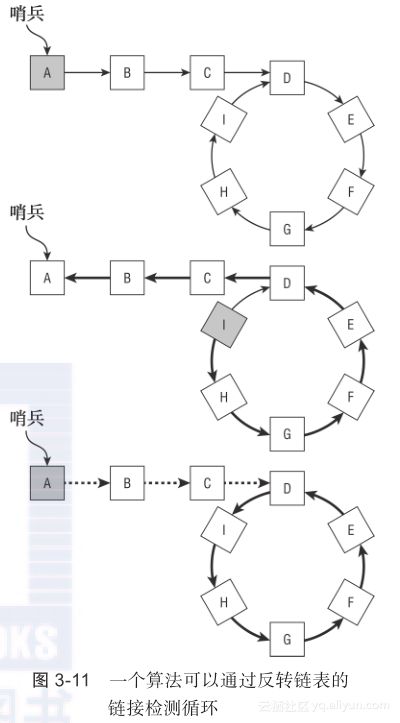

在图3-11的顶端的子图显示出了原始链表，并以阴影来表示算法中的哨兵点，即在该算法中被访问过的第一个单元格。该算法通过链表移动，扭转了链接。
在图3-11的中间的子图显示，它已经达到了单元格I。接下来，算法顺着单元格I逆转到单元格D。然后它遵循从单元格D到单元格C，B和A的反向链路遍历。由于它遵循这些关系，算法再次反转它们，得到的链表如图3-11底部子图所示。这里已两度逆转的链接，用虚线箭头表示。
在此时，该算法返回到链表中的第一个单元格，所以它知道该链表包含一个循环。请注意，新的链表和原来那个基本相同，不同的是新的链表中在循环中的链接是颠倒的。
因为该算法必须扭转链表两次，它以下列方法开始扭转链表：

此伪代码通过链表移动，扭转链接，并返回最后一个被访问的结点，也是在翻转后的链表中的第一个结点。
下面的算法利用之前的伪代码来确定链表中是否包含一个循环：

该算法调用ReverseList方法来扭转链表，并得到了逆转后链表的第一个单元格。然后，它再次调用ReverseList重新扭转链表，恢复到其原始的链接。
如果sentinel和翻转后的链表的第一个单元格是一样的，该算法返回true。如果sentinel和逆转后的链表中的第一个单元格不同，该算法返回false。
该算法遍历链表两次，一次反向链接，而一次进行恢复，所以它执行2×N＝O(N)个步骤。该算法运行花费O(N)的时间，而不需要额外的空间。不幸的是，它只能检测回路；它不提供一个方法来打破它们。接下来的算法解决了这个问题，尽管它可能是这里描述的算法中最令人困惑的。
3.8.5　乌龟和兔子
这个算法被称为龟兔赛跑算法或者是弗洛伊德循环查找算法，弗洛伊德在19世纪60年代发明了这一种算法。这一种算法本身并不复杂，但是它的解释实在让人很困惑，所以如果不想看到复杂的数学论证，可以跳过接下来的伪代码。
这个算法一开始设定两个对象“乌龟”和“兔子”，它们从链表的开始以不同的速度沿着链表遍历。乌龟每一步移动一个单元格，兔子每一步移动两个单元格。
如果兔子走到一个空的链接上，意味着这个链表有一个终点，也就是说没有循环。
如果这个链表包含一个循环，兔子最终一定会进入这个循环，并且开始沿着循环不停的绕圈。
与此同时，乌龟缓慢的沿着链表爬行，最终它也会进入这个循环。此时，兔子和乌龟都处于这个循环之中。
令T表示乌龟在进入循环之前经过的步数，令H为T步后兔子在循环中的位置距离循环开始点的距离，正如图3-12中显示。令L表示循环中的单元格的数目。

在图3-12中，T＝4，H＝4，且L＝5。
因为兔子行走的速度是乌龟的两倍，它在行走T步之前就到达了循环。它之后又经过了循环里的T个单元格到达了如图3-12中的位置，这可以总结为下面的重要事实#1。
重要事实#1：
如果在循环里的移动穿过T个单元格，则会在距离进入循环的位置H个单元格的地方停下。

注意，如果L远远小于T，兔子可能已经奔波循环好几圈。举例来说，如果T是102并且L为5，乌龟在102步之后到达循环。兔子在51步后到达循环，度过接下来的50步（100格）要经过环路20圈，然后在循环中多移动了一个步骤（两个单元格）。在这种情况下，H＝2。
接下来的问题是，“什么时候兔子赶上乌龟？”当乌龟进入循环中，兔子是在H单元格上，如图3-12所示。因为乌龟和兔子都在一个循环中，所以也可以认为兔子在乌龟L-H个单元格之后。因为兔子移动两格，而乌龟只移动一格，每次移动它和乌龟之间的距离都会接近一格。这意味着兔子将在L-H次移动后追上乌龟。
在图3-12中，H＝4，L＝5，所以当它们相遇在单元格E时，兔子将只走了5－4＝1步。
这意味着，乌龟只在循环之中走了一步就相遇了。当两只动物相遇，他们在循环中走的路程之差为L－（L－H）＝H。这是重要的事实#2。
重要事实#2：
当兔子抓到乌龟的时候，这两只动物除了循环的开始之外经过了L－H个单元格。

现在，如果从相会点让乌龟移动H个单元格，乌龟将会停在循环开始的位置，这样可以找到这个循环的起始点。不幸的是，因为不知道H值，所以不能简单地将乌龟移动那么远。
不过，从重要事实#1可以知道，如果乌龟绕着圈移动T个单元格，它最终将停在距离开始的位置H个单元格处。在这种情况下，乌龟最终将在循环的开始处停下！
不幸的是，同样不知道T的值，所以不能简单地把乌龟移动那么远。但是，如果让兔子从链表的开头重新开始，并让它的步速为每一步一个单元格，而不是两步（这可能是在循环了这么久之后它累了），它也将在穿过T个单元格后到达循环的开始处。这意味着两个动物将在穿越T个单元格后，在循环开始点再次相遇。
下面的伪代码在一个较高的层面上描述了这个算法：
1）让乌龟在链表中每一步一格地移动。让兔子在链表中每一步两格地移动。
2）如果兔子找到一个空链接，则链表中没有回路，所以停止。
3）否则，当兔子赶上乌龟时，让兔子从链表的开始重新跑，每一步移动一个单元格，然后继续移动乌龟，每步一格。
4）当乌龟和兔子再次见面时，它们是在循环的开始处。让兔子在循环的起点进行休息，而乌龟大约需要多循环一个圈。当乌龟的Next指针为那个兔子所在的单元格时，乌龟是在循环的末尾。
5）要打破回路，将乌龟所在的单元格的Next指针设为null。
注　笔者从来没有见过真正需要使用龟兔赛跑算法的程序。如果足够细心，没有理由让一个链表被偶然的环路破坏掉。然而，检测环路似乎是一种流行的面试问题和谜题，所以了解一下这类问题的解决方案也是极有帮助的。
3.8.6　双向链表中的循环问题
在一个双向链表中检测环路很容易。如果有一个环路，某处的Next指针跳回链表中前面的部分。而这个Next指针所指单元格的Prev指针却指向一个更早的单元格，而不是当前的这个单元格。
因此，检测循环时只需要遍历一遍链表，对于每个单元格，检验cell.Next.Prev==cell。
假设这些单元格构成了一个普通的双向链表并且如果存在循环的话，其必然是普通循环。如果Next和Prev完全不同步，这个做法只能添乱，而不能帮忙解决问题。相比带循环的双向链表，不如说这是检测通过同一个单元格两个线程的示例。