(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting
计划完成深度学习入门的126篇论文第十篇,多伦多大学的Geoffrey Hinton·和Alex Krizhevsky使用一种新的regularization方法Dropout。
ABSTRACT&INTRODUCTION
摘要
具有大量参数的深度神经网络是非常强大的机器学习系统。然而,在这样的网络中,过拟合是一个严重的问题。大型网络的使用也很缓慢,通过在测试时结合许多不同的大型神经网络的预测,很难处理过拟合问题。Dropout是解决这个问题的一种技术。其关键思想是在训练过程中随机地从神经网络中删除单元(以及它们的连接)。这就避免了单位之间的过度协作。在训练过程中,从指数数量的不同的\变薄“网络”中退出样本。在测试时,只需使用一个权重较小的未稀释网络,就可以很容易地近似所有这些稀释网络的预测平均值的效果。这大大减少了过拟合,与其他正则化方法相比有了很大的改进。我们发现dropout改善了神经网络在视觉、语音识别、文档分类和计算生物学等监督学习任务中的性能,在许多基准数据集上都取得了最先进的结果。
Keywords: neural networks, regularization, model combination, deep learning
介绍
深度神经网络包含多个非线性隐含层,这使得它们成为非常具有表现力的模型,能够学习输入和输出之间非常复杂的关系。然而,在训练数据有限的情况下,这些复杂的关系中有很多都是采样噪声的结果,即使是在训练集中,即使是来自相同的分布,它们也会存在于训练集中,而不是真实的测试数据中。这导致了过拟合和许多方法已开发减少它。其中包括一旦验证集的性能开始变差就停止训练,引入各种各样的体重惩罚,如L1和L2正规化和soft weight sharing(Nowlan和Hinton, 1992)。
在无限计算的情况下,调整“固定大小模型”的最佳方法是对参数的所有可能设置进行平均预测,并对每个设置进行加权给定训练数据后验概率。对于简单或小型模型,这有时可以很好地近似(Xiong 2011;Salakhutdinov, 2008),但是我们希望使用更少的计算来接近贝叶斯黄金标准的性能。我们建议通过近似一个平均加权的几何平均值来实现这一点,该平均值是对共享参数的指数型学习模型的预测。
模型组合几乎总能提高机器学习方法的性能。然而,对于大型神经网络,对许多单独训练的网络的输出进行平均的想法显然是非常昂贵的。当单个模型彼此不同时,组合多个模型是最有帮助的,为了使神经网络模型不同,它们要么具有不同的架构,要么对不同的数据进行训练。训练许多不同的架构是困难的,因为为每个架构找到最优的超参数是一项艰巨的任务,并且训练每个大型网络需要大量的计算。此外,大型网络通常需要大量的训练数据,而且可能没有足够的数据在不同的数据子集上训练不同的网络。即使一个人能够训练许多不同的大型网络,在测试时使用它们是不可行的,因为在应用程序中快速响应非常重要。
Dropout是一种解决这两个问题的技术。它防止了过拟合,并提供了一种近似地将多种不同的神经网络结构以指数形式有效结合的方法。“drop - out”是指在神经网络中删除(隐藏的和可见的)单元。通过删除一个单元,我们的意思是从网络中临时删除它,以及它所有的传入和传出连接,如图1所示。要删除哪些单元的选择是随机的。在最简单的情况下,每个单元以固定的概率p被保留,独立于其他单元,其中p可以使用验证集选择,也可以简单地设置为0.5,这对于广泛的网络和任务来说似乎接近最优。然而,对于输入单元,保留的最佳概率通常更接近于1而不是0.5。
将dropout应用到神经网络中相当于从神经网络中抽取一个变细的“网络”。稀疏网络由所有drop存活的单元组成(图1b)。一个有n个单元的神经网络,可以看作是2^n个可能的神经网络的集合。这些网络共享权重,因此参数的总数仍然是O(n^2)或更少。对于每个训练用例的每个表示,将对一个新的瘦网络进行采样和训练。因此,训练一个drop神经网络可以看作是训练一个2^n个具有广泛权重共享的瘦网络集合,每个瘦的网络很少接受训练,如果有的话。
在测试时,显式地对许多瘦模型的预测进行平均是不可行的。然而,一个非常简单的近似平均法在实践中效果很好。该方法的思想是在测试时使用单一的神经网络而不丢失。该网络的权值是训练权值的缩小版。如果一个单元在训练过程中以概率p保留,则该单元输出的权值在测试时乘以p,如图2所示。这可以确保对于任何隐藏单元,预期输出(在训练时用于删除单元的分布下)与测试时的实际输出相同。通过这样的扩展,2^n个共享权值的网络可以组合成一个单独的神经网络,在测试时使用。我们发现,与其他正则化方法相比,在测试时使用这种近似平均方法训练一个有dropout的网络,可以显著降低在各种分类问题上的泛化误差。
dropout的概念并不局限于前馈神经网络。它可以更广泛地应用于图形模型,例如Boltzmann机器。本文引入了误差限制的玻尔兹曼机模型,并与标准限制的玻尔兹曼机模型进行了比较。实验表明,drop - dropout RBMs在某些方面优于标准RBMs。
本文的结构如下。第2节描述了这个想法的动机。第3节描述了以前的相关工作。第4节正式描述了drop模型。第五部分给出了一种训练丢包网络的算法。在第6节中,我们展示了我们的实验结果,我们将dropout应用于不同领域的问题,并将其与其他形式的正则化和模型组合进行比较。第7节分析了drop对神经网络不同性质的影响,描述了dropout如何与网络超参数相互作用。第8节描述了drop - RBM模型。在第9节中,我们探讨了dropout边缘化的概念。在附录A中,我们提供了一个实用指南用于训练dropout nets。这包括在训练dropout net时选择超参数的实际考虑的详细分析。
Motivation
dropout的动机来自于性别在进化中的作用理论(Livnat et al., 2010)。
有性生殖包括取父母一方一半的基因和另一方一半的基因,加入少量随机突变,然后将它们结合起来产生后代。无性繁殖的另一种选择是用父母基因的一个稍微变异的副本创造一个后代。无性繁殖应该是一种优化个体适应性的更好方法,这似乎是合理的,因为一组良好的基因在一起工作得很好,可以直接传递给后代。另一方面,有性生殖可能会破坏这些共同适应的基因集,特别是如果这些基因集很大,而且直觉上,这会降低已经进化出复杂共同适应的生物体的适应性。然而,有性生殖是最先进的生物进化的方式。
有性生殖优越性的一种可能解释是,从长期来看,自然选择的标准可能不是个体的适应性,而是基因的混合能力。一组基因能够很好地与另一组随机基因一起工作的能力使它们更健壮。由于一个基因不能依赖于一大群伴侣每时每刻都在场,它必须学会自己做一些有用的事情,或者与少量其他基因合作。根据这一理论,有性生殖的作用不仅是让有用的新基因在人群中传播,而且通过减少复杂的共适应来促进这一过程,这种共适应会减少新基因改善个体适应性的机会。同样,在dropout训练的神经网络中,每一个隐藏的单元都必须学会使用随机选择的其他单元样本。这将使每个隐藏单元更加健壮,并推动它自己创建有用的特性,而不需要依赖其他隐藏单元来纠正错误。然而,隐藏在一个层中的单位仍然会学会彼此做不同的事情。有人可能会认为,通过对每个隐藏单元进行多次复制,网络将变得健壮,从而防止dropout,但这是一个糟糕的解决方案,其原因与复制代码是处理噪声信道的糟糕方法完全相同。
dropout的一个密切相关但略有不同的动机来自于对成功阴谋的思考。10个阴谋,每个阴谋涉及5个人,可能比一个大阴谋,需要50个人都正确发挥自己的作用,更好的方式来制造浩劫。如果条件不变,有足够的排练时间,大阴谋可以顺利进行,但在非平稳条件下,阴谋越小,继续运作的机会越大。复杂的共适应可以在训练集上训练得很好,但是在新的测试数据上,它们比实现相同目的的多个简单的共适应更容易失败。
Related Work
dropout可以解释为一种通过在神经网络的隐藏单元中加入噪声使其正则化的方法。Vincent et al.(2008, 2010)曾在去噪自动编码器(DAEs)的环境中使用过在单位状态中添加噪声的概念将其加入到自动编码器的输入单元中,训练网络重构无噪声输入。我们的工作扩展了这一思想,表明dropout也可以有效地应用于隐藏层,并且可以解释为模型平均的一种形式。我们还证明了添加噪声不仅对无监督特征学习有用,而且可以推广到有监督学习问题。事实上,我们的方法可以应用于其他基于神经的架构,例如Boltzmann机器。虽然5%的噪声通常最适合DAEs,但我们发现在测试时应用的权重调整程序使我们能够使用更高的噪声级别。去掉20%的输入单元和50%的隐藏单元通常是最优的。
由于dropout可以看作是一种随机正则化技术stochastic regularization,因此很自然地考虑它的确定性对应物,这种对应物是通过将噪声边缘化而得到的。在本文中,我们证明,在简单的情况下,drop可以被解析边缘化,从而得到确定性正则化方法。最近,van der Maaten等人(2013)也研究了不同指数族噪声分布对应的确定性正则化器,包括dropout(drop - out noise)(他们称之为\blankout noise)。但是,它们对输入应用噪声,并且只探索没有隐藏层的模型。Wang和Manning(2013)提出了一种通过消除Dropout噪声来加速Dropout的方法。Chen等(2012)在去噪自编码器的背景下探讨了边缘化问题。
在dropout中,我们在噪声分布下随机地最小化损失函数。这可以看作是最小化预期损失函数。Globerson和Roweis先前的工作(2006);Dekel等人(2010)研究了另一种情况,即当对手选择放弃哪些单位时,损失最小。在这里,不是一个噪声分布,最大单位数可以下降是固定的。然而,这项工作也没有探索隐藏单元的模型。
Model Description
本节描述drop神经网络模型。考虑一个神经网络L隐藏层。设![]() 索引网络的隐藏层。设z(l)为层l的输入向量,y(l)为层l 的输出向量(y(0) = x为输入向量)。W (l)和b(l)为层l的权值和偏差,标准神经网络的前馈操作(图3a)可描述为(对于
索引网络的隐藏层。设z(l)为层l的输入向量,y(l)为层l 的输出向量(y(0) = x为输入向量)。W (l)和b(l)为层l的权值和偏差,标准神经网络的前馈操作(图3a)可描述为(对于![]() 和任何隐藏的单元i)
和任何隐藏的单元i)
f是任何激活函数,例如,f (x) = 1 = (1 + exp (−x))。
dropout后,前馈操作变为(图3b)
这里 * 表示元element-wise的乘积。对于任意层l, r(l)是一个独立伯努利随机变量的向量每个随机变量的概率都是p = 1。这个向量被采样,并与该层的输出y(l)相乘,从而得到更细的输出ye(l)。然后将稀释后的输出用作下一层的输入。这个过程应用于每一层。这相当于从一个更大的网络中抽取一个子网络。对于学习,损失函数的导数通过子网络反向传播。在测试时,将权重按比例缩放为![]() ,如图2所示。所得到的神经网络使用dropout。
,如图2所示。所得到的神经网络使用dropout。
Learning Dropout Nets
1. Backpropagation
dropout神经网络可以采用类似于标准神经网络的随机梯度下降法进行训练。唯一的区别是,对于小批量的每个训练案例,我们通过去掉单元来对一个变薄的网络进行取样。训练用例的前向和后向传播只在这个稀疏的网络上进行。每个参数的梯度在每个小批中的训练用例上平均。任何不使用参数的训练情况都会使该参数的梯度为零。随机梯度下降的改进方法有动量法、退火学习速率法和L2权值衰减法。这些被发现对dropout神经网络也是有用的。
发现了一个特殊形式的正规化为Dropout,特别有用的规范约束的权向量在每个隐藏单元由一个固定的常数c的上界。换句话说,如果w代表权重的向量事件在任何隐藏的单元,约束条件下的神经网络优化![]() 。这期间施加约束优化的w情绪投射到一个球的表面半径c,每当w出去。这也被称为最大范数正则化,因为它意味着任何权值的范数可以取的最大值是c,常数c是一个可调的超参数,它是由一个验证集确定的。Max-norm正则化以前被用于协同过滤(Srebro and Shraibman, 2005)。即使在不使用dropout的情况下,它也能显著提高深度神经网络的随机梯度下降训练的性能。
。这期间施加约束优化的w情绪投射到一个球的表面半径c,每当w出去。这也被称为最大范数正则化,因为它意味着任何权值的范数可以取的最大值是c,常数c是一个可调的超参数,它是由一个验证集确定的。Max-norm正则化以前被用于协同过滤(Srebro and Shraibman, 2005)。即使在不使用dropout的情况下,它也能显著提高深度神经网络的随机梯度下降训练的性能。
虽然dropout本身有显著的改善,但是随着maxnorm的正则化,使用dropout,大的衰减学习率和高动量比仅仅使用dropout有显著的提高。一种可能的解释是,将权向量限制在一个半径固定的球内,使之有可能使用一个巨大的学习率,而不存在权值爆炸的可能性。drop提供的噪声允许优化过程探索权重空间的不同区域,否则很难达到这些区域。随着学习率的降低,优化的步骤会缩短,从而减少探索,最终达到最小值。
2. Unsupervised Pretraining
神经网络可以使用RBMs (Hinton and Salakhutdinov, 2006)、autoencoders (Vincent et al., 2010)或Deep Boltzmann Machines (Salakhutdinov and Hinton, 2009)进行预训练。预处理是利用未标记数据的一种有效方法。在某些情况下,由反向传播的finetuning进行的预先训练比随机初始化finetuning带来的性能显著提高。
dropout可以应用于使用这些技术预先培训的finetune网络。训练前的程序保持不变。训练前获得的权重应该按比例增加1=p。这保证了每个单元在随机丢包情况下的期望输出与训练前的输出相同。我们最初担心drop的随机性可能会抹去预训练权值中的信息。当fine tuning过程中使用的学习率与随机初始化网络的最佳学习率相当时,就会发生这种情况。然而,当学习率被选择为较小时,我们似乎保留了预先训练的权值中的信息,相对于finetuning时不使用dropout,我们能够在最终泛化误差方面得到改善。
Experimental Results
针对不同领域数据集的分类问题,我们训练了drop - neural network。我们发现,与不使用dropout的神经网络相比,dropout提高了所有数据集的泛化性能。表1简要描述了数据集。数据集是::
我们选择了一组不同的数据集来证明dropout是一种改进神经网络的通用技术,并不特定于任何特定的应用领域。在这一部分,我们给出了一些关键的结果,表明dropout有效性。附录B提供了所有实验和数据集的更详细描述。
1. Results on Image Data Sets
我们使用5个图像数据集来评估MNIST, SVHN, CIFAR-10, CIFAR-100, ImageNet。这些数据集包括不同的图像类型和训练集大小。在所有这些数据集上实现最先进结果的模型都使用dropout。
1.1 MNIST
MNIST数据集包含28个×28像素手写数字图像。任务是将图像分类为10位类。表2对比了dropout与其他技术的性能。置换不变量的最佳神经网络未使用dropout或无监督预训练的设置误差约为1.60% (Simard et al., 2003)。通过误差降至1,35%。将物流单元替换为修正的线性单元(ReLUs) (Jarrett et al., 2009)进一步将误差降低到1,25%。再加上最大范数正则化,将其降至1,06%。增加网络的规模会带来更好的结果。一个2层8192个单元的神经网络误差为0.95%。请注意,这个网络有6 500多万个参数,正在对6万个大小的数据集进行训练。使用标准正则化方法和提前停止训练这种规模的网络以获得良好的泛化误差是非常困难的。另一方面,Dropout,防止过拟合,即使在这种情况下。它甚至不需要提前停止。Goodfellow等(2013)通过将ReLU单元替换为maxout单元,结果可以进一步提高到0.94%。所有的dropout使用p = 0.5为隐藏单位和p = 0.8为输入单位。更多实验细节见附录B.1。使用RBMs和Deep Boltzmann机器预先训练的drop - nets也进行了改进,如表2所示。DBM|预训练dropout - net的测试误差为0.79%,是置换不变集的最佳性能。我们注意到,利用二维空间信息,利用标准训练集图像的畸变版本对训练集进行扩充,可以获得更好的结果。我们在更有趣的数据集上展示了dropout在该设置下的有效性。
为了测试dropout的鲁棒性,我们对不同结构的网络进行了分类实验,所有的超参数(包括p)都保持不变。图4显示了随着培训的进行,这些不同体系结构的测试错误率。同样的结构训练与没有dropout有显著不同的测试误差,正如看到的两个单独的集群的轨迹。dropout在所有体系结构中都有巨大的改进,而不需要使用针对每个体系结构进行特定调优的超参数。
1.2 Street View House Numbers
Street View House Numbers (SVHN)数据集(Netzer et al., 2011)由谷歌Street View采集的房屋编号彩色图像组成。图5a展示了这个数据集中的一些图像示例。我们在实验中使用的数据集部分由32 - 32张颜色图像组成,这些图像大致以房屋号码中的一个数字为中心。任务是识别那个数字。对于该数据集,我们将dropout应用于卷积神经网络(LeCun et al., 1989)。我们发现最好的架构有三个卷积层,然后是两个完全连接的隐藏层。所有隐藏的单位都是ReLUs。每个卷积层都是max-pooling层。附录B.2更详细地描述了体系结构。将drop应用于网络的所有层,保留隐藏单元的概率为p = (0:9;0:75;0:75;0:5;0:5;0:5)对于网络的不同层(从输入层到卷积层再到全连通层)。卷积层和全连通层的权值均采用极大范数正则化。表3比较了不同方法的结果。我们发现卷积网络优于其他方法。最好的卷积网络不使用dropout,其错误率为3.95%。仅将drop添加到完全连接的层中可以将错误降低到3.02%。在卷积层中加入dropout,进一步将误差降低到2.55%。
使用maxout单元可以获得更多的增益。通过在卷积层中添加dropout(3.02%到2.55%)获得的额外性能收益值得注意。有人可能会认为,由于卷积层没有很多参数,过拟合不是问题,因此dropout不会有太大影响。然而,较低层的dropout仍然有帮助,因为它为较高的完全连接层提供了噪声输入,从而防止它们过拟合。
1.3 CIFAR-10 and CIFAR-100
CIFAR-10和CIFAR-100数据集分别由10个类别和100个类别的32x32幅彩色图像组成。图5b显示了该数据集的一些图像示例,附录B.3给出了数据集、输入预处理、网络架构等实验细节的详细描述。表4显示了不同方法在这些数据集上得到的错误率。Snoek等(2012)在不增加任何数据的情况下,利用贝叶斯超参数优化算法在CIFAR-10上获得了14.98%的错误率。在全连通层中使用dropout将误差降低到14.32%,在每一层中添加dropout将误差进一步降低到12.61%。Goodfellow等(2013)通过将ReLU单元替换为maxout单元,误差进一步降低到11.68%。在CIFAR-100上,dropout将误差从43.48%降低到了37.20%,这是一个巨大的改进。两个数据集都没有使用数据扩充(除了dropout)。
1.4 ImageNet
ImageNet是一个包含超过1500万张高分辨率图像的数据集,属于大约2.2万个类别。从2010年开始,作为Pascal视觉对象挑战赛的一部分,一年一度的ImageNet大规模视觉识别挑战赛(ILSVRC)已经举行。在这个挑战中使用了ImageNet的一个子集,在1000个类别中每个类别中大约有1000个图像。由于类别的数量相当大,通常报告两个错误率:top-1和top-5,其中top-5错误率是测试图像中正确标签不在模型认为最可能出现的5个标签中的比例。图6显示了我们的模型对一些测试图像所做的预测。
ILSVRC-2010是唯一一个有测试集标签的ILSVRC版本,所以我们的大部分实验都是在这个数据集上进行的。表5比较了不同方法的性能。dropout在很大程度上优于其他方法。架构和实现细节详见Krizhevsky等人(2012)。
我们基于卷积网络和dropout的模型赢得了ILSVRC-2012比赛。由于测试集的标签不可用,我们将在最终提交的测试集上报告我们的结果,并包含模型不同变体的验证集结果。表6显示了比赛结果。基于标准视觉特征的最佳方法的错误率在前5名中约为26%,而drop的卷积网络的测试错误率约为16%,这是一个惊人的差异。图6显示了我们的模型所做预测的一些示例。我们可以看到,该模型做出了非常合理的预测,即使它的最佳猜测是不正确的。
2. Results on TIMIT
接下来,我们将dropout应用到语音识别任务中。我们使用TIMIT数据集,该数据集由680位发言者的录音组成,涵盖了美国英语的8种主要方言,在一个可控的无噪音环境中阅读10个语音丰富的句子。在21个log-filter bank帧的窗口上训练dropout- neural network来预测中心帧的label。没有执行与speaker相关的操作。附录B.4描述了数据预处理和培训细节。表7 drop - neural比较网络与其他模型。6层网络的电话错误率为23:4%。dropout进一步提高到21.8%。我们还从预先训练的重量开始训练退网。一个4层网络预训练与一堆rbm得到一个电话错误率22.7%。dropout下降到19.7%。类似地,对于8层网络,错误从20.5%减少到19.7%。
3. Results on a Text Data Set
为了验证dropout在文本域中的有效性,我们使用dropout网络训练了一个文档分类器。我们使用了路透社rcv1数据集的一个子集,该数据集收集了80多万篇来自路透社的新闻专线文章。这些文章涉及各种主题。任务是将一袋文档的单词表示形式划分为50个互不相关的主题。附录B.5更详细地描述了设置。我们最好的神经网络没有使用dropout得到的错误率为31.05%。dropout低到29.62%。我们发现,与视觉和语音数据集相比,这种改进要小得多。
4. Comparison with Bayesian Neural Networks
dropout可以被看作是一种对多个共享权值的指数模型进行等权平均的方法。另一方面,Bayesian神经网络(Neal, 1996)是对神经网络结构和参数空间进行模型平均的合适方法。在dropout中,每个模型的权重是相等的,而在Bayesian神经网络中,每个模型的权重是考虑先验和模型与数据的拟合程度,这是更正确的方法。贝叶斯神经网络在解决医学诊断、遗传学、药物发现和其他计算生物学应用等数据稀缺领域的问题时非常有用。然而,贝叶斯神经网络训练缓慢,很难扩展到非常大的网络规模。此外,在测试时从许多大型网络获得预测是很昂贵的。另一方面,dropout神经网络在测试时的训练和使用要快得多。在本节中,我们报告了在一个已知贝叶斯神经网络性能良好并获得最新结果的小数据集上,将贝叶斯神经网络与drop - neural network进行比较的实验。目的是分析dropout与Bayesian神经网络相比损失多少。我们使用的数据集(Xiong et al., 2011)来自遗传学领域。其任务是基于RNA特征预测选择性剪接的发生。选择性剪接是哺乳动物组织细胞多样性的重要原因。预测不同条件下某些组织中交替剪接的发生对于理解许多人类疾病是重要的。鉴于RNA的特性,这项任务是预测生物学家关心的三种相关剪接事件的概率。评价指标是代码质量,它衡量的是目标和预测概率分布(越高越好)之间负的KL发散。附录B.6包括数据集和此性能指标的详细描述。
表8总结了不同模型在该数据集上的性能。Xiong等(2011)使用贝叶斯神经网络来完成这项任务。正如预期的那样,我们发现贝叶斯神经网络比dropout表现得更好。然而,我们发现dropout比标准神经网络的性能有显著提高,并且优于其他所有方法。这个数据集的挑战是防止过拟合,因为训练集的大小很小。防止过拟合的一种方法是使用主成分分析降低输入维度。然后,可以使用标准技术,如支持向量机或逻辑回归。然而,通过drop,我们可以避免过拟合而不需要降维。与贝叶斯网络中的几十个单元相比,dropout网络非常大(隐藏单元有1000个)。由此可见,dropout具有较强的正则化效应。
5. Comparison with Standard Regularizers
为防止神经网络过拟合,提出了几种正则化方法。这些包括L2的重量衰减(更普遍的是Tikhonov正则化(Tikhonov, 1943)), lasso (Tibshirani, 1996), kl稀疏性和max-norm正则化。drop可以看作是神经网络正则化的另一种方法。在本节中,我们使用MNIST数据集将drop与这些正则化方法中的一些方法进行了比较。
我们使用不同正则化的随机梯度下降方法对相同的网络架构(784-1024-1024-2048-10)和ReLUs进行了训练。表9显示了结果。利用验证集得到了与每种正则化相关的不同超参数的值(衰减常数、目标稀疏性、dropout、max-norm上界)。我们发现dropout结合max-norm正则化得到的泛化误差最小。
Salient Features
上一节描述的实验提供了强有力的证据,证明dropout是一种改进神经网络的有效技术。在本节中,我们将仔细研究dropout如何影响神经网络。我们分析了dropout对特征产生的质量的影响。我们看到dropdropout影响隐藏单元激活的稀疏性。我们还可以看到dropout的优势是如何随着保留单元的概率、网络的大小和训练集的大小而变化的。
1. Effect on Features
在一个标准的神经网络中,每个参数接收到的导数告诉它应该如何变化,从而减少最终的损失函数,给定所有其他单位在做什么。因此,单位可能会在某种程度上改变,以弥补其他单位的错误。这可能导致复杂的协同适应。这反过来又会导致过拟合,因为这些共适应不会推广到看不见的数据。我们假设对于每一个隐藏单元,drop通过使其他隐藏单元的存在不可靠来阻止共适应。因此,一个隐藏的单位不能依赖其他特定的单位来纠正它的错误。它必须在其他隐藏单元提供的各种不同上下文中表现良好。为了直接观察这种效果,我们观察了通过训练视觉任务的神经网络学习的第一级特征。
图7a显示的是MNIST上的一个自动编码器学习到的特征,它有一个256个线性整流单元的隐藏层,没有丢失。图7b显示了一个相同的autoencoder所学习的特性,该autoencoder在隐藏层使用drop, p = 0.5。两种自动编码器的测试重构误差相似。然而,图7a所示的特征显然是相互适应的,以便产生良好的重建。每个隐藏的单元本身似乎并没有检测到有意义的特性。另一方面,在图7b中,隐藏的单元似乎可以检测图像不同部分的边缘、笔画和斑点。这表明dropout确实会破坏共适应,这可能是它导致较低泛化错误的主要原因。
2. Effect on Sparsity
我们发现,作为dropout的副作用,即使没有稀疏诱导正则化的存在,隐藏单元的激活也变得稀疏。因此,dropout会自动导致稀疏表示。为了观察这种效果,我们使用上一节中训练的自动编码器,并从测试集中随机抽取一个小批数据,查看隐藏单元激活的稀疏性。图8a和图8b比较了这两个模型的稀疏性。在一个好的稀疏模型中,对于任何数据情况,应该只有少数几个高度激活的单元。此外,跨数据用例的任何单元的平均激活应该很低。为了评估这两个特性,我们为每个模型绘制两个直方图。对于每个模型,左边的直方图显示了隐藏单元的平均激活度在整个小批处理中的分布。右边的直方图显示了隐藏单元的激活分布。
通过对激活直方图的比较,我们可以看到,与图8a相比,图8b中激活程度较高的隐藏单元较少,从图8b中的显著质量可以看出对于不使用dropout的网为零。对于dropout网络,平均激活度也较小。对于无dropout的自动编码器,其隐藏单元的整体平均激活度接近2.0,而使用drop时则下降到0.7左右。
3. Effect of Dropout Rate
dropout具有可调的超参数p(网络中保留一个单元的概率)。在本节中,我们将探讨改变这个超参数的效果。比较是在两种情况下进行的。
1. 隐藏单元的数量保持不变。
2. 改变隐藏单元的数量,使dropout后保留的隐藏单元的期望数量保持不变。
在第一种情况下,我们训练相同的网络架构,不同的dropout。我们使用784-2048-2048-2048-10架构。没有输入丢失被使用。图9a显示了作为p的函数得到的测试误差。如果架构保持不变,p越小意味着在训练过程中打开的单元越少。由此可见,由于训练误差也比较大,导致了拟合不足。我们看到随着p的增加,误差减小。变得平坦当![]() 然后增加随着p变得接近于1。
然后增加随着p变得接近于1。
另一个有趣的设置是第二种情况,在这种情况下,数量pn保持不变,其中n是任何特定层中隐藏的单元数。这意味着p小的网络会有大量的隐藏单元。因此,在应用dropout之后,在不同的体系结构中出现的单元的期望数量将是相同的。然而,测试网络的大小是不同的。在我们的实验中,我们为前两个隐藏层设置pn = 256,为最后一个隐藏层设置pn = 512。图9b显示了作为p的函数得到的测试误差。我们注意到,与图9a相比,p的小值的误差幅度减小了很多(当p = 0.1时,误差从2.7%下降到1.7%)。接近0.6的p值对于pn的选择似乎是最好的,但是我们通常的默认值0.5接近于最优值。
4. Effect of Data Set Size
对一个好的正则化器的一个测试是,它应该使在小数据集上训练大量参数的模型能够得到良好的泛化误差。本节探讨前馈网络使用dropout时改变数据集大小的影响。以标准方式训练的巨大神经网络在小数据集上过度适用。为了看看dropout是否有帮助,我们在MNIST上进行分类实验,改变给网络的数据量。
这些实验的结果如图10所示。随机从MNIST训练集中选取大小为100、500、1K、5K、10K、50K的数据集,对所有数据集使用相同的网络架构(784-1024-1024-2048-10)。p = 0.5的dropout在所有隐藏层执行,p = 0.8的dropout在输入层执行。可以观察到,对于非常小的数据集(100,500),dropout没有任何改进。该模型具有足够的参数,即使所有的噪声都是由dropout产生的,它也能对训练数据进行过拟合。的大小
5. Monte-Carlo Model Averaging vs. Weight Scaling
我们提出的有效的测试时间程序是通过缩小训练神经网络的权值来做一个近似的模型组合。对模型进行平均的一种昂贵但更正确的方法是对每个测试用例使用dropout对k个神经网络进行采样,并对它们的预测进行平均。![]() 、蒙特卡罗模型平均值接近真实模型平均值。从经验上看,需要多少个样本k才能满足近似平均法的性能是很有趣的。通过计算不同k值的误差,我们可以看到有限样本均值的错误率接近真实模型均值的错误率有多快。
、蒙特卡罗模型平均值接近真实模型平均值。从经验上看,需要多少个样本k才能满足近似平均法的性能是很有趣的。通过计算不同k值的误差,我们可以看到有限样本均值的错误率接近真实模型均值的错误率有多快。
我们再次使用MNIST数据集,通过平均k个随机采样神经网络的预测来进行分类。图11为不同k值下得到的测试错误率,与权重比例法得到的错误率进行对比(如图水平线所示)。可以看出,在k = 50左右,蒙特卡罗方法变得和近似方法一样好。此后,蒙特卡罗方法略优于近似方法,但在一个标准差内。这表明权重比例法是一个相当好的方法。
Conclusion
Dropout是一种通过减少过拟合来改进神经网络的技术。标准的反向传播学习构建了脆弱的共适应,这些共适应适用于训练数据,但不能推广到不可见的数据。随机Dropout打破了这些共同适应使任何特定隐藏单元的存在不可靠。该技术可以提高神经网络在对象分类、数字识别、语音识别、文档分类和计算生物学数据分析等广泛应用领域的性能。这表明drop是一种通用的技术,并不特定于任何领域。使用dropout的方法在SVHN、ImageNet、CIFAR-100和MNIST上实现了最先进的结果。同时,Dropout也大大提高了标准神经网络在其他数据集上的性能。
这个概念可以扩展到受限的玻尔兹曼机器和其他图形模型。dropout的核心思想是取一个容易过度拟合且重复采样的大模型,并从中训练较小的子模型。RBMs很容易适应这个框架。我们开发了Dropout RBMs,并通过实验证明它们具有某些理想的性质。
Dropout的缺点之一是增加了训练时间。Dropout网络的训练时间通常是相同结构的标准神经网络的2-3倍。这种增长的一个主要原因是参数更新非常嘈杂。每个训练案例都有效地尝试训练不同的随机体系结构。因此,正在计算的梯度不是将在测试时使用的最终架构的梯度。因此,培训需要很长时间也就不足为奇了。然而,这种随机性可能防止过拟合。这就造成了过度适应和训练时间之间的平衡。训练时间越长,Dropout越高,过拟合越少。然而,在不受随机性影响的情况下,获得drop的一些好处的一种方法是将噪声边缘化,从而期望得到一个与drop过程相同的正则化器。我们证明了对于线性回归,这个正则化器是L2正则化的修正形式。对于更复杂的模型,如何得到等效的正则化器并不明显。加速Dropout是今后工作的一个有趣方向。
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第1张图片](http://img.e-com-net.com/image/info8/6d0e880225a046a39c800a0707ac4442.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第2张图片](http://img.e-com-net.com/image/info8/f6a32ab3b5f347e79e8be29987c405b7.jpg)
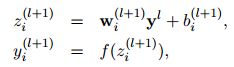
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第3张图片](http://img.e-com-net.com/image/info8/7de497c6e8814e189309b73e4159f004.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第4张图片](http://img.e-com-net.com/image/info8/a8b1f63e98eb40448772531b1e2cde90.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第5张图片](http://img.e-com-net.com/image/info8/ca9883ada6984a2c8bfb28c6749037bf.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第6张图片](http://img.e-com-net.com/image/info8/1f769f8ff1a44bc8b87fceacdd4fea6b.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第7张图片](http://img.e-com-net.com/image/info8/4dee07604c5641a0828ba1a9d8b17c7e.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第8张图片](http://img.e-com-net.com/image/info8/72f999eb7d1e48eda3268124bfc734a5.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第9张图片](http://img.e-com-net.com/image/info8/cf5003e3ec414d48a216ab8bca5e6138.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第10张图片](http://img.e-com-net.com/image/info8/30f85e53a2424de98e53745eb582c5d5.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第11张图片](http://img.e-com-net.com/image/info8/b21628bf0338406b8bcefbe231406185.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第12张图片](http://img.e-com-net.com/image/info8/1e5a54338c934b22aebcf1878399fe3d.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第13张图片](http://img.e-com-net.com/image/info8/26baec976c5c47ffbb9488d651c8fec3.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第14张图片](http://img.e-com-net.com/image/info8/5ffdf0f147c849efbe2322a6a8c2d7d1.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第15张图片](http://img.e-com-net.com/image/info8/8e0bb9f3a9b24791b010d73e4ac4e206.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第16张图片](http://img.e-com-net.com/image/info8/b76e57a690b44f25a3c3f35a9dd07696.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第17张图片](http://img.e-com-net.com/image/info8/cbaf650470ac4d958496687ffab7cce3.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第18张图片](http://img.e-com-net.com/image/info8/8b4931fff8cb4261b0b62aea29b3646d.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第19张图片](http://img.e-com-net.com/image/info8/b6f07a16285845d8800c02ed25938831.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第20张图片](http://img.e-com-net.com/image/info8/a4cf8ef434154a22a4bf3e2f2f8ef264.jpg)
![(10) [JMLR14] Dropout: A Simple Way to Prevent Neural Networks from Overfitting_第21张图片](http://img.e-com-net.com/image/info8/df2d72e2490740359baf892d732ac769.jpg)