吴恩达机器学习课后习题ex8 异常检测(python实现)
异常检测
- 二维数据
- 高维数据
在本练习中,您将实现异常检测算法来检测服务器计算机中的异常行为。这些特性测量每台服务器的吞吐量(mb/s)和响应延迟(ms)。当您的服务器正在运行时,您收集了m=307个它们的行为示例,因此有一个未标记的数据集。您怀疑这些示例中的绝大多数是服务器正常运行的“正常”(非异常)示例,但也可能有一些服务器在此数据集中异常运行的示例。您将使用高斯模型来检测数据集中的异常示例。您将首先从二维数据集开始,该数据集将允许您可视化算法正在执行的操作。在该数据集上,您将拟合高斯分布,然后找到概率非常低的值,因此可以认为是异常值。之后,将异常检测算法应用于具有多个维度的较大数据集。
二维数据
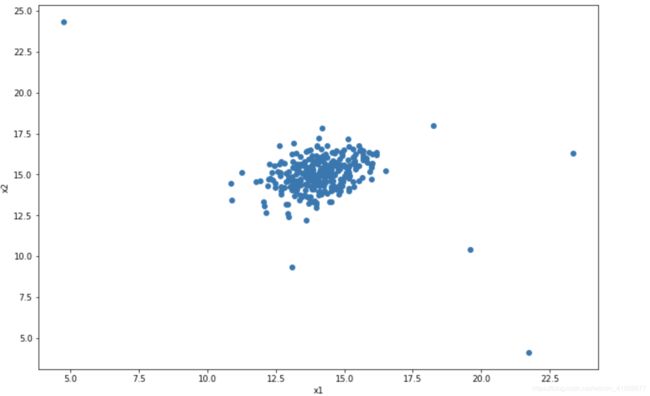
首先导入数据集,并可视化观察
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat
mat1=loadmat('data/ex8data1.mat')
X=mat1['X']
Xval=mat1['Xval']
yval=mat1['yval']
fig,ax=plt.subplots(figsize=(12,8))
ax.scatter(X[:,0],X[:,1],)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
plt.show()
def gussian(x,mu,sigma):
p=(1/np.sqrt(2*np.pi*sigma))*np.exp(-(x-mu)**2/2*sigma)
return np.prod(p,axis=1)
#也可以使用多元高斯分布模型计算概率
def multi_gussian(x,mu,sigma):
p=np.zeros((len(x),1))
n=len(mu)
if np.ndim(sigma)==1:
sigma=np.diag(sigma)
for i in range(len(x)):
p[i]=(2*np.pi)**(-n/2)*np.linalg.det(sigma)**(-1/2)*np.exp(-0.5*(x[i,:]-mu).T@np.linalg.inv(sigma)@(x[i,:]-mu))
return p
估计参数mu和sigma
def estimate_param(x):
mu=x.mean(axis=0)
sigma=x.mean(axis=0)
return mu,sigma
mu,sigma=estimate_par(X)
mu,sigma
(array([14.11222578, 14.99771051]), array([1.83263141, 1.70974533]))
mu.shape,sigma.shape
((2,), (2,))
可视化,显示拟合高斯分布的轮廓。从图中可以看出,大多数例子都在概率最高的区域,而异常例子则在概率较低的区域。
def plot(x,mu,sigma):
x=np.linspace(5,25,100)
xx,yy=np.meshgrid(x,x) #(100,100)
z=np.c_[xx.flatten(),yy.flatten()] #(10000,2)
zz=multi_gussian(z,mu,sigma)
zz=z.reshape(xx.shape)
levels=[10**h for h in range(-20,0,3)]
plt.contour(xx,yy,zz,levels)
plt.scatter(X[:,0],X[:,1])
plt.show()
#计算F1
def computeF1(yval,pval):
#yval 真实值 pval 预测值
tp,fp,fn,tn=0,0,0,0
for i in range(len(yval)):
if yval[i]==pval[i]:
if pval[i]==1:
tp+=1
else:
tn+=1
else:
if pval[i]==1:
fp+=1
else:
fn+=1
precision=tp/(tp+fp) if (tp+fp) else 0
recall=tp/(tp+fn) if (tp+fn) else 0
f1=2*precision*recall/(precision+recall) if (precision+recall) else 0
return f1
#寻找合适的阈值
def select_threshold(yval,pval):
rang=np.linspace(min(pval),max(pval),1000)
bestf1=0
bestthr=0
for i in rang:
ypre=(pval<i).astype(float)
f1=computeF1(yval,ypre)
if f1>bestf1:
bestf1=f1
bestthr=i
return bestf1,bestthr
计算pval,这里需要注意:使用的是训练集的平均值和方差!,而不是交叉验证集的!!!
pval=gussian(Xval,mu,sigma)
bestf1,bestthr=select_threshold(yval,pval)
bestthr,bestf1
在交叉验证集上求出阈值
(0.00015745207777512692, 0.8750000000000001)
可视化,用阈值和概率值进行比较,圈出训练集上的异常点
p=gussian(X,mu,sigma)
anomaly_dot=np.where(p<bestthr)
anomaly_dot
(array([300, 301, 303, 304, 305, 306]),)
plot(X,mu,sigma)
plt.scatter(X[anomaly_dot,0],X[anomaly_dot,1],s=80,facecolors='none', edgecolors='r')
高维数据
mat2 = loadmat( 'data/ex8data2.mat' )
X2 = mat2['X']
Xval2, yval2 = mat2['Xval'], mat2['yval']
X2.shape,Xval2.shape
(1000, 11) (100,11)
mu2,sigma2=estimate_par(X2)
p=gaussian_distribution(X2,mu2,sigma2)
pval=gaussian_distribution(Xval2,mu2,sigma2)
bestthr2,bestf1_2=select_threshold(yval2,pval)
bestthr2,bestf1_2
(1.3786074982000235e-18, 0.6153846153846154)
anomaly_dot2=np.where(p<bestthr2)
len(anomaly_dot2[0])
117
所以训练集上总共有117个异常点。