机器学习01线性回归模型

机器学习01-线性回归模型

1、线性回归

参考周志华老师的《机器学习》中对线性回归的定义:
给定数据集$D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m))\}$，其中$x_i=x_{i1};x_{i2};,...;x_{id},y_i\in R.$ “线性回归”(linear regression)试图学得一个线性模型以尽可能准确地预测实值输出标记.

下面通过一个散点图和其拟合的线性模型来对线性回归进行分析.

在上图中, 我们通过观察$x$轴和$y$轴的散点具有一定的线性关系, 而”线性回归“的目的就是找出一条用来描述$x$轴和$y$轴关系的线. 对于一元回归来说, 学习的是一条直线, 对于多元线性回归来说就是学习一个面或超平面.

2、线性回归模型

在理解线性回归概念的基础上，我们需要从数学的角度来建立线性回归模型。
在自变量$x_i$和因变量$y_i$具有一定线性关系的数据中，线性回归模型试图学得：
$$h(x_i)=w^T{x}_i+b\text{，使得}h(x_i)\approx y_i$$
其中$w=(w_1;w_2;\dots ;w_d).w\text{和}b学的之后,模型也就确定了.$

通过观察学习的线性模型和散点图，我们可以发现直线并没有完全拟合数据，而是存在一定的误差。该假设即为线性模型函数，其中含有两个参数 $w$与$b$ 。
通常，在线性回归模型中，我们会添加偏置项$x_0=1$，令$w_0\ast x_1=b$从而使得模型函数为：
$$h(x_i)=w^T{x}_i,\text{此时}w=(w_1;w_2;\dots ;w_d)$$

3、损失函数

回归任务中最常用的性能度量就是均方误差(Mean Squared Error):
$$E(h;D)=\frac{1}{m}\sum _{i=1}^m(f(x_i)-y_i{)}^2.$$
在这里，出于运算的角度，我们采用如下函数作为损失函数:
$$J(w)=\frac{1}{2m}\sum _{i=1}^m(h(x_i)-y_i{)}^2,i=1,2,\dots ,m$$
目标函数$J(w)$描述了所有训练样本实际值与预测值之间的均方误差，而我们的目的就是求解能够使得该误差$J(w)$值最小的参数$w=(w_1;w_2;\dots ;w_d).$

4、优化算法之梯度下降法

通过观察损失函数：
$$J(w)=\frac{1}{2m}\sum _{i=1}^m(h(x_i)-y_i{)}^2=\frac{1}{2m}\sum _{i=1}^m(w^T{x}_i-y_i{)}^2$$
可以看成$J(w)$是关于$w$的二次函数参考图形如下：

可看出$J(w)$对每个w存在最小点，即$\frac{\Delta J(w)}{\Delta w}=0.$
在求解使得误差$J(w)$值最小的参数$w=(w_1;w_2;\dots ;w_d)$中，我们采用梯度下降法，即每次向误差变小的方向走一步，直到误差收敛。其基本思想如下：
  （1）从某个$w$开始一般设置为0;
  （2）不断修改$w$ ,以使得 $J(w)$ 越来越小，直到最低点。
  其算法过程为：
   repeat {
   $w:=w-\alpha \frac{\Delta J(w)}{\Delta w}$
   }
其中 α 为学习率（learning rate），也就是每一次的“步长”； $\frac{\Delta J(w)}{\Delta w}$是方向，也可以看做是二次函数上每一点的切线斜率，可以使得整体上是朝着最小值点的方向进行。参见下图进行理解：

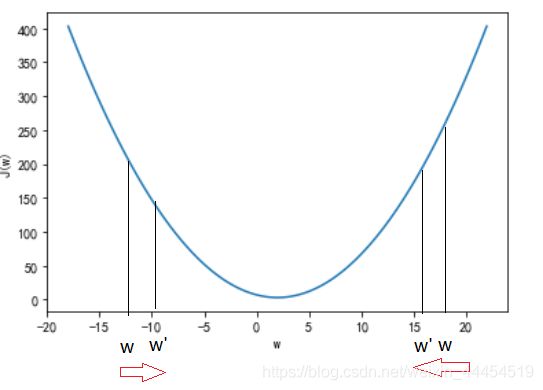
由上述公式可以看出, 当算法达到迭代次数或者损失函数达到收敛便可停止. 其中步长$\alpha$由人为指定, 迭代次数也可以人为指定, 损失函数达到收敛可以通过损失函数最后一个和倒数第二个数的差值小于某个数来求解，即$cost(-1)-cost(-2)<ϵ$, 其中$\epsilon可以自己指定.

5、自编代码

5.1 数据
本次数据采用自变量为房子面积和居式、因变量为价格的回归模型，其中数据为.txt文本类型, 采用三列，分别表示房子面积、几居式和价钱。其数据读取如下：

# 1、加载数据
def loadDataSet(filename):
    X = [] # 用来保存特征
    Y = [] # 保存因变量
    with open(filename, 'rb') as f:
        for idx, line in enumerate(f):
            line = line.decode('utf-8').strip()# 对读到的每一行进行两端去空格
            if not line: # 判断是否读完数据
                continue
            eles = line.split() # 将每一行数据拆分成特征和因变量
            if idx == 0:
                numFea = len(eles)
            eles = list(map(float, eles))
                
            X.append(eles[:-1]) # 将每一行中的特征添加进X列表中
            Y.append([eles[-1]])# 将每一行中的自变量添加进Y列表中
    return np.array(X), np.array(Y)

originX, Y = loadDataSet("./data/houses.txt") # 导入房价相关数据
print(originX.shape, Y.shape) # 输出样本数和特征数

5.2 数据标准化
主要针对参差不齐的X数据进行标准化，采用正规化方法，基于原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。其公式如下:
$$x_i^{\prime }=\frac{(x_i-mean(x))}{std(x)}$$
数据标准化参考代码如下:

# 2、标准化数据
def standarize(X):
    m, n = X.shape
    values = {} # 保存每一列的mean和std，便于对预测数据进行标准化
    for j in range(n):
        features = X[:, j]
        meanVal = features.mean(axis=0) # 对每一个特征求平均值
        stdVal = features.std(axis=0)   # 对每一个特征求方差
        values[j] = [meanVal, stdVal]   # 将每一个特征的平均值和方差放入values列表中
        if stdVal != 0:
            X[:, j] = (features - meanVal) / stdVal # 对数据进行标准化
        else:
            X[:, j] = 0
    return X, values

m,n = originX.shape
X, values = standarize(originX.copy())
X = np.concatenate((np.ones((m,1)), X), axis=1) # 对X特征值添加偏置项x0=1
print(X.shape, Y.shape) # 打印样本数和特征数
print(X[:3], values) # 打印特征值、特征平均值和方差

5.3 定义假设函数
假设函数就是我们假设w已知，通过w和x值来求解预测y值，其代码如下:

# 3、定义假设函数
def h(theta, X):
    return np.dot(X, theta) # 通过矩阵点积，对每个样本的所有特征与w进行相乘

5.4 定义损失函数
假设函数就是我们假设w已知，通过w和x值来求解预测y值，其代码如下:

# 4、定义损失函数
def J(theta, X, Y):
    m = len(X)
    # 通过矩阵点积实现所有样本"均方误差"
    return np.sum(np.dot((h(theta, X) - Y).T, (h(theta, X) - Y))/(2 * m))

5.5 定义梯度函数并对数据进行学习

# 5、定义梯度函数
def bgd(alpha, X, Y, maxloop, epsilon):
    m, n = X.shape
    theta = np.zeros((n, 1)) # 初始化所有w为0
    count = 0 # 初始化迭代次数
    converged = False # 判断是否收敛
    cost = np.inf # 损失初始化为无穷大
    costs = [J(theta, X, Y),] # 将每次迭代的损失添加进costs数列，便于后面对比
    thetas = {}
    for i in range(n):
        thetas[i] = [theta[i, 0],] # 用来保存每次迭代的w值,其中字典键代表第几个特征
    while count <= maxloop:# 判断迭代次数
        if converged: # 判断是否收敛
            break
        count += 1

        # n个参数同时计算更新值
        theta = theta - alpha *1.0/m *np.dot(X.T, (h(theta, X) - Y))
        for j in range(n):
            thetas[j].append(theta[j, 0])

        cost = J(theta, X, Y)
        costs.append(cost)
        if abs(costs[-1] - costs[-2]) < epsilon: # 判断收敛
            converged = True
    return theta, thetas, costs
# 模型学习
alpha = 1 # 学习率
maxloop = 10000 # 最大迭代次数
epsilon = 0.000001 # 前后两次cost花费相差值收敛标志
resault = bgd(alpha, X, Y, maxloop, epsilon)
theta, thetas, costs = resault
print(theta, thetas, costs)

5.6 进行预测测试

# 4、预测
normalizedSize = (70 - values[0][0])/values[0][1]
normalizedBr = (2 - values[1][0])/values[1][1]
predicateX = np.matrix([[1, normalizedSize, normalizedBr]])
price = h(theta, predicateX)
price

5.7 绘制拟合平面

# 绘制拟合平面
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
import matplotlib.ticker as mtick

fittingFig = plt.figure(figsize=(16, 12)) # 设置画布大小
title = 'bgd: rate=%.3f, maxloop=%d, epsilon=%.3f \n'%(alpha,maxloop,epsilon)
ax=fittingFig.gca(projection='3d')

xx = np.linspace(0,200,25)
yy = np.linspace(0,5,25)
zz = np.zeros((25,25))
for i in range(25):
    for j in range(25):
        normalizedSize = (xx[i]-values[0][0])/values[0][1] # 对x进行标准化
        normalizedBr = (yy[j]-values[1][0])/values[1][1] # 对y进行标准化
        x = np.matrix([[1,normalizedSize, normalizedBr]])
        zz[i,j] = h(theta, x)
xx, yy = np.meshgrid(xx,yy)
ax.zaxis.set_major_formatter(mtick.FormatStrFormatter('%.2e'))
# 画拟合平面
ax.plot_surface(xx, yy, zz, rstride=1, cstride=1, cmap=cm.rainbow, alpha=0.1, antialiased=True)
xs = originX[:, 0].flatten()
ys = originX[:, 1].flatten()
zs = Y[:, 0].flatten()
ax.scatter(xs, ys, zs, c='b', marker='o')# 在三维空间中画散点图
ax.set_xlabel(u'面积')
ax.set_ylabel(u'卧室数')
ax.set_zlabel(u'估价')
# plt.show()

5.8 绘制代价函数随迭代次数图

# 8、绘制代价函数
%matplotlib inline
errorsFig = plt.figure()
ax = errorsFig.add_subplot(111)
ax.yaxis.set_major_formatter(mtick.FormatStrFormatter('%.2e'))
ax.plot(range(len(costs)), costs)
ax.set_xlabel(u'迭代次数')
ax.set_ylabel(u'代价函数')

6、调用sklearn库进行线性模型回归

# 1、读取数据
import pandas as pd
salary_data = pd.read_csv("./data/Salary_Data.csv") # 读取薪水数据
print(salary_data.head(5))

# 2、通过sklearn回归模型对工作年限和薪水之间的关系进行拟合
from sklearn.linear_model import LinearRegression
LR = LinearRegression().fit(a.iloc[:, 0:1],a.iloc[:, 1:])# 进行模型训练
print(LR.coef_)# 回归系数（斜率）
print(LR.intercept_) # 截距项

# 3 输出线性回归模型的评价系数R^2,
R2 = LR.score(salary_data.iloc[:, 0:1],salary_data.iloc[:, 1:])

# 4 画出实际数据散点图和拟合直线
from matplotlib import pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置中文显示
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['axes.unicode_minus'] = False # 设置负号正确显示
plt.xlabel("工作年限") # 输出x轴标签
plt.ylabel("薪资") # 输出y轴标签
plt.scatter(a.iloc[:, 0:1],a.iloc[:, 1:]) # 画实际值的散点图

X = np.linspace(0, 12, 20) # 画拟合直线需要的X值
Y = X * LR.coef_[0][0] + LR.intercept_[0] # 训练的模型直线Y值
plt.plot(X, Y) # 画拟合直线

附数据：
链接：https://pan.baidu.com/s/1dX6UOrfBUvCCDwNTQI8WBg
提取码：ei0b
本博文供交流学习所用，参考了大量别人的博文和书本.

参考

[1] https://www.cnblogs.com/lliuye/p/9120839.html
[2]《机器学习》 周志华著
[3] https://www.cnblogs.com/eric666666/p/11312048.html
[4] https://baijiahao.baidu.com/s?id=1643175053031902456&wfr=spider&for=pc
[5] Cmd Markdown 公式指导手册
[6] 三种常用数据标准化方法. https://blog.csdn.net/bbbeoy/article/details/70185798