机器学习02决策树模型
1、什么是决策树
参考李航老师的《统计学习方法》中对决策树的定义:
分类决策树模型是一种描述对实例进行分类的属性结构。决策树有结点(node)和有向边(direceted edge)组成。结点有两种类型:内部结点(internal node)和叶结点(leaf node)。内部结点表示一个特征或属性,叶结点表示一个类。
下面参考周志华老师的《机器学习》中以二分类任务为例子来解释决策树模型的决策过程:
决策树是基于树结构来进行决策的,假如我们要对“是否好瓜”进行判断时,会经过一系列的判断来做决策。我们先看它的颜色,如果是青绿色;我们再看它的根蒂是什么形状,如果是蜷缩;我们再判断它敲起来是什么声音,最后得出最后决策,这是个”好瓜“。例子中树结构模型如下图:
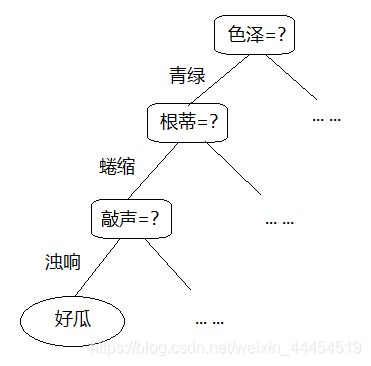
一颗决策树包含一个根结点、若干个内部结点和若干个叶结点;决策树学习的目的是为了产生一颗泛化能力强,即处理未见示例能力强的决策树,其处理流程遵循“分而治之”策略。其伪代码如下:
输入:训练集 D = {(x1,y1),(x2,y2),...,(xm,ym)}
属性集 A = {a1,a2,...,ad}
过程:函数TreeGenerate(D, A)
生成结点node
if D中结点全属于同一类别C:
将node标记为C类叶结点
return
elif A = 空集 or D中样本在A上取值相同:
将node标记为叶结点,其类别标记为D中样本数最多的类
return
else:
从A中选择最优划分属性a*
for a* in A: # 每次从A中取一个属性
为node生成一个分支,令Dv表示D中在a*上取值为a*=v的样本子集;
if Dv为空:
将分支结点标记为叶结点,其类别标记为D中样本最多的类
return
else:
以TreeGenerate(Dv, A\{a*})为分支结点
输出:以node为根结点的一棵决策树
决策树的生成是一个递归过程,上述算法中有三种情形会导致递归返回:(1)当前结点包含的样本全属于同一类别;(2)当前属性集为空,或是所有样本在所有属性上的取值相同;(3)当前结点包含的样本集合为空,不能划分。
2、如何选择最优划分属性
2.1 信息增益(ID3)
“信息熵”是度量样本集合纯度最常用的一种指标。一般来说,信息熵的值越小,样本的纯度越高。假定当前样本集合D中第 k k k类样本所占的比例为 p k ( k = 1 , 2 , . . . , ∣ γ ∣ ) p_k(k=1,2,...,|\gamma|) pk(k=1,2,...,∣γ∣),则D的信息熵定义为:
E n t ( D ) = − ∑ k = 1 ∣ γ ∣ p k l o g 2 p k Ent(D)=-\sum_{k=1}^{|\gamma|}p_klog_2p_k Ent(D)=−k=1∑∣γ∣pklog2pk
假定离散属性 a = { a 1 , a 2 , . . . , a V } a=\{a_1,a_2,...,a_V\} a={a1,a2,...,aV},其中 a a a属性第 v v v个取值为 a v a^v av的所有样本,记为 D v D^v Dv。我们通过对每个属性的取值增加概率权重 ∣ D v ∣ ∣ D ∣ \frac{|D^v|}{|D|} ∣D∣∣Dv∣,从而计算 D v D^v Dv的信息熵,同时可以计算出用属性 a a a对样本集D进行划分获得的“信息增益(information gain)”
G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ E n t ( D v ) Gain(D,a)=Ent(D)-\sum_{v=1}^V\frac{|D^v|}{|D|}Ent(D^v) Gain(D,a)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)
一般来说,信息增益越大,意味着使用属性 a a a来进行划分所获得的“纯度提升”越大。所以在属性划分上每次选择属性 a ∗ = a r g m a x G a i n ( D , a ) a^*=arg\ maxGain(D,a) a∗=arg maxGain(D,a)作为划分属性,这就是著名的ID3决策时学习算法用的属性划分准则。
2.2 增益率(C4.5)
实际中,信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响, C 4.5 C4.5 C4.5决策树算法使用“增益率(gain ratio)”来选择最优划分属性。其中增益率定义为:
G a i n r a t i o ( D , a ) = G a i n ( D , a ) I V ( a ) , Gain_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}, Gainratio(D,a)=IV(a)Gain(D,a),
其中,
I V ( a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ l o g 2 ∣ D v ∣ ∣ D ∣ IV(a)=-\sum_{v=1}^V\frac{|D^v|}{|D|}log_2\frac{|D^v|}{|D|} IV(a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣
成为属性 a a a的“固有值”(intrinsic value),属性 a a a的可能取值数目越多,则V越大,所以增益率准则对可取值数目较少的属性有所偏好。因此, C 4.5 C4.5 C4.5算法并没有直接选用增益率最大的候选划分属性,而是使用了一个启发式:先从候选属性中赵卒后信息增益高于平均水平的属性,再从中选择增益率最高的。
2.3 基尼指数(CART)
CART决策树使用“基尼指数”(Gini index)来选择划分属性,数据集D的纯度可用基尼值来度量:
G i n i ( D ) = ∑ k = 1 ∣ γ ∣ ∑ k ′ ≠ k p k p k ′ = 1 − ∑ k = 1 ∣ γ ∣ p k 2 Gini(D)=\sum_{k=1}^{|\gamma|}\sum_{k'\neq k}p_k p_{k'}=1-\sum_{k=1}^{|\gamma|}p_{k^2} Gini(D)=k=1∑∣γ∣k′=k∑pkpk′=1−k=1∑∣γ∣pk2
G i n i ( D , a ) Gini(D,a) Gini(D,a)反应了从数据集中随机取两个样本,类别标记不一致的概率。因此,Gini(D)越小,数据集D的纯度越高。
属性 a a a的基尼指数定义为:
G i n i i n d e x ( D , a ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ G i n i ( D v ) Gini_index(D,a)=\sum_{v=1}^{V}\frac{|D^v|}{|D|}Gini(D^v) Giniindex(D,a)=v=1∑V∣D∣∣Dv∣Gini(Dv)
在使用基尼指数准则作为最佳属性划分,通常选用基尼指数最小的属性作为最优划分属性,即 a ∗ = a r g m i n G i n i _ i n d e x ( D , a ) a^*=arg\ min\ Gini\_index(D,a) a∗=arg min Gini_index(D,a)
3、剪枝处理
剪枝是决策树学习算法对付“过拟合”的主要手段,在决策树学习过程当中,结点划分不断重复有时会导致分支过多,决策树学习的太好了,以致于把训练集自身的一些特点当作所有数据都具有的一般性质而导致过拟合。因此,可主动去掉一部分分支来降低过拟合的风险。
一个学习后的模型通常会用测试集来预测模型的正确率,从而反映模型的优劣。下图是一个学习完全的决策树,其中,这个模型也有一个测试集的正确率用来反映这个模型的优劣。
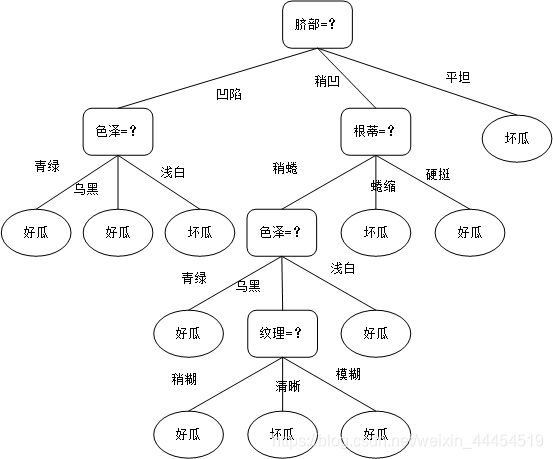
3.1 预剪枝
在上图中划分前,所有样例点都集中在根结点。
- 从根结点开始不划分,并标记为叶子结点,其类别标记为训练样例数最多的类别,然后用这个模型对测试集进行分类,如果这个模型比完全模型的正确率还要高,则不进行划分,如果没有优化,则进行下一步划分。
- 下面的每一次结点划分前,都将当下结点标记为叶子结点,其类别标记为训练例数最多的类别,然后用前后两个模型进行对比优劣,决定是否进行下一步的划分。
3.2 后剪枝
在决策树训练完全的模型上,所有样例点都已经被完全划分了。
- 从完全决策树的最底层开始往上剪枝,每次剪掉的叶子结点的父节点标记为叶节点,其类别标记为训练样例数最多的类别,然后用这个模型与完全决策树模型进行优劣对比,决定是否要进行剪枝。
- 每次从下面往上面的每个中间结点进行剪枝处理,通过对比剪枝前后两个模型的优劣来决定是否要进行剪枝操作。
4、属性连续和缺失值处理
4.1 连续属性处理
对于连续属性值,通常采用的是二分法,C4.5决策树中对连续属性值就是二分法。
在样本集D和出现了n个不同的连续值的属性 a a a,对属性 a a a进行排序,记为 { a 1 , a 2 , . . . , a n } \{a^1,a^2,...,a^n\} {a1,a2,...,an},以 a = t a=t a=t点将样本分为两类 D t − D_{t-} Dt−和 D t + D_{t+} Dt+,对含有n个不同值的连续属性 a a a,对 t t t的候选点集合为:
T a = { a i + a i + 1 2 ∣ 1 ≤ i ≤ n − 1 } T_a=\{\frac{a^i+a^{i+1}}{2}|1\leq i\leq n-1\} Ta={2ai+ai+1∣1≤i≤n−1}
这样就得到了 n − 1 n-1 n−1个t候选点,然后对每个候选点得到不同的两类 D t − D_{t-} Dt−和 D t + D_{t+} Dt+,然后通过特征选择算法对比不同 t t t分类的属性 a a a的优劣,来决定最好的 t t t值。
4.2 属性缺失值处理
对缺失值的处理,在样本足够多并且去掉缺失值不影响总体的情况下,我们一般都采用去掉含有缺失值的样本。
在现实中,简单的去掉缺失值的样本,无疑是对数据信息极大的浪费。在给定训练集 D D D和属性 a a a,我们作如下表示:
D ~ \tilde D D~:表示 D D D在属性 a a a上没有缺失值的样本子集;
D ~ v \tilde D^v D~v:表示 D ~ \tilde D D~中属性 a a a取值为 a v a^v av的样本子集;
D ~ k \tilde D^k D~k:表示 D ~ \tilde D D~中属于第 k k k类的样本子集。
我们为每个样本赋予一个权重:
ρ = ∑ x ∈ D ~ w x ∑ x ∈ D w x \rho =\frac{\sum_{x\in \tilde D}w_x}{{\sum_{x\in D}w_x}} ρ=∑x∈Dwx∑x∈D~wx
p ~ k = ∑ x ∈ D ~ k w x ∑ x ∈ D ~ w x \tilde p_k =\frac{\sum_{x\in \tilde D_k}w_x}{{\sum_{x\in \tilde D}w_x}} p~k=∑x∈D~wx∑x∈D~kwx
r ~ v = ∑ x ∈ D ~ v w x ∑ x ∈ D ~ w x \tilde r_v=\frac{\sum_{x\in \tilde D^v}w_x}{{\sum_{x\in \tilde D}w_x}} r~v=∑x∈D~wx∑x∈D~vwx
对属性 a a a,
ρ \rho ρ表示无缺失值样本所占的比例;
p ~ k \tilde p_k p~k表示无缺失值样本中第k类所占的比例;
r ~ v \tilde r_v r~v表示无缺失值样本中在属性 a a a上取值 a v a^v av的样本所占的比例;
对于含有缺失值的样本,我们将信息增益的计算式推广为:
G a i n ( D , a ) = ρ × G a i n ( D ~ , a ) = ρ × ( E n t ( D ~ ) − ∑ v = 1 V r ~ v E n t ( D v ) ) Gain(D,a)=\rho \times Gain(\tilde D,a)=\rho \times (Ent(\tilde D)-\sum_{v=1}^V\tilde r_vEnt(D^v)) Gain(D,a)=ρ×Gain(D~,a)=ρ×(Ent(D~)−v=1∑Vr~vEnt(Dv))
其中:
E n t ( D ~ ) = − ∑ k = 1 ∣ γ ∣ p ~ k l o g 2 p ~ k Ent(\tilde D)=-\sum_{k=1}^{|\gamma|}\tilde p_k log_2 \tilde p_k Ent(D~)=−k=1∑∣γ∣p~klog2p~k
5、决策树的自编代码
本文代码参考《统计学习方法》代码实现。
据第1小结中的伪代码,我们将采用递归方法实现决策树。
其基本思路如下:
- 结点设计self.root判断是否是叶子结点,如果是叶子结点,self.label标记最后的样本类别;如果是内部结点,通过使用feature标记内部结点分类的属性;self.tree字典表示子树,其中键为属性分类,值为子结点(就是一颗子树)。
- 递归出口:
1)子集全属于同一类别Ck,返回Ck类别的叶结点;
2)属性集为空,返回子集中最大的类作为该结点的类标记;
3)类别信息增益小于某个阈值epsilon,返回子集中最大的类作为该结点的类标记;
4)对属性中的每个属性分类进行递归构建结点。
代码实现:
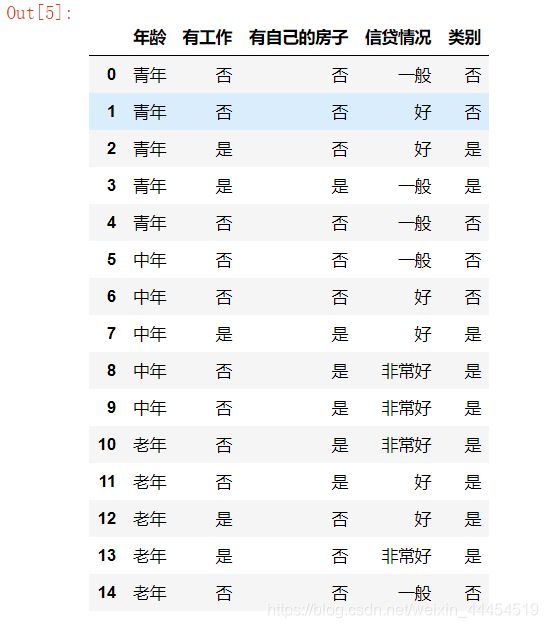
# 1、采用《统计学习方法》中决策树章节上的数据
import pandas as pd
def create_data():
datasets = [['青年', '否', '否', '一般', '否'],
['青年', '否', '否', '好', '否'],
['青年', '是', '否', '好', '是'],
['青年', '是', '是', '一般', '是'],
['青年', '否', '否', '一般', '否'],
['中年', '否', '否', '一般', '否'],
['中年', '否', '否', '好', '否'],
['中年', '是', '是', '好', '是'],
['中年', '否', '是', '非常好', '是'],
['中年', '否', '是', '非常好', '是'],
['老年', '否', '是', '非常好', '是'],
['老年', '否', '是', '好', '是'],
['老年', '是', '否', '好', '是'],
['老年', '是', '否', '非常好', '是'],
['老年', '否', '否', '一般', '否'],
]
labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别']
# 返回数据集和每个维度的名称
return datasets, labels
datasets, labels = create_data()
data_train = pd.DataFrame(datasets, columns=labels) # 将训练数据封装成pd.DataFrame类型
# 2、定义决策树结点
class Node:
def __init__(self, root=True, label=None, feature_name=None, feature=None):
self.root = root # 判断是否是叶子结点
self.label = label # 标记叶子结点类别
self.feature_name = feature_name
self.feature = feature # 标记分类结点属性类别
self.tree = {} # 子树
self.result = { # 返回每个结点信息
"label":self.label,
"feature": self.feature,
"tree": self.tree
}
def __repr__(self):
return "{}".format(self.result)
def add_node(self, val, node): # 通过属性类别为键,子树为值添加结点
self.tree[val] = node
def predict(self, features):
if self.root is True: # 判断是否是单节点树
return self.label # 返回预测值
return self.tree[features[self.feature]].predict(features) # 从根结点开始判断
# 3、定义决策树类
class DTree:
def __init__(self, epsilon=0.1):
self.epsilon = epsilon # 定义属性经验信息增益阈值
self._tree = {} # 定义一个树
# 信息熵计算
@staticmethod
def calc_ent(datasets):
data_length = len(datasets)
label_count = {}
for i in range(data_length):
label = datasets[i][-1]
if label not in label_count:
label_count[label] = 0
label_count[label] += 1
ent = -sum([(p/data_length) * log(p/data_length, 2) for p in label_count.values()])
return ent
# 经验信息熵计算
def cond_ent(self, datasets, axis=0):
data_length = len(datasets)
feature_sets = {}
for i in range(data_length):
feature = datasets[i][axis]
if feature not in feature_sets:
feature_sets[feature] = []
feature_sets[feature].append(datasets[i])
cond_ent = sum([(len(p)/data_length)* self.calc_ent(p) for p in feature_sets.values()])
return cond_ent
# 通过信息熵和经验信息熵,计算属性的信息增益
@staticmethod
def info_gain(ent, cond_ent):
return ent - cond_ent
# 计算datasets数据集中最大信息增益的属性
def info_gain_train(self, datasets):
count = len(datasets[0]) - 1
ent = self.calc_ent(datasets)
best_feature = []
for c in range(count):
c_info_gain = self.info_gain(ent, self.cond_ent(datasets, axis=c))
best_feature.append((c, c_info_gain))
best_ = max(best_feature, key=lambda x: x[-1])
return best_
def train(self, train_data):
"""
input: 数据集D(pd.DataFrame)
output:决策树T
"""
_, y_train, features = train_data.iloc[:, :-1], train_data.iloc[:, -1], train_data.columns[:-1]
# 1、若D中实例属于同一类Ck, 将类Ck作为结点的类标记,定义出口1
if len(y_train.value_counts()) == 1:
return Node(root=True, label=y_train.iloc[0])
# 2、若A为空,D中实例树最大的类Ck作为该结点的类标记,定义出口2
if len(features) == 0:
return Node(root=True, label=y_train.value_counts().sort_values(ascending=False).index[0])
# 3、计算最大信息增益Ag为信息增益最大的特征
max_feature, max_info_gain = self.info_gain_train(np.array(train_data))
max_feature_name = features[max_feature] # 最大信息增益属性名
# 4、Ag的信息增益小于阈值eta, 将D中是实例数最大的类Ck作为该结点的类表示,定义出口3
if max_info_gain < self.epsilon:
return Node(root=True, label=y_train.value_counts().sort_values(ascending=False).index[0])
# 5、对属性Ag的子结点进行构建
node_tree = Node(root=False, feature_name=max_feature_name, feature=max_feature) 构建属性Ag结点
feature_list = train_data[max_feature_name].value_counts().index # 属性Ag中所有不同的属性值
for f in feature_list:
sub_train_df = train_data.loc[train_data[max_feature_name] == f].drop([max_feature_name], axis=1) # 对属性Ag中属性值为f的属性样本,剔除属性f列,构建子集
# 6、递归生成树
sub_tree = self.train(sub_train_df) # 对属性Ag属性值为f递归构建子树
node_tree.add_node(f, sub_tree) # 将子结点加入树中
return node_tree
def fit(self, train_data): # 重写训练函数
self._tree = self.train(train_data)
return self._tree
def predict(self, X_test): # 重写预测函数
return self._tree.predict(X_test)
# 4、对数据进行训练
import pandas as pd
import numpy as np
dt = DTree()
tree = dt.fit(data_train) # 对data_train数据进行训练
print(tree)
# 5、预测, 结果如下图
dt.predict(['老年', '否', '否', '一般'])
6、调用sklearn库实现决策过程
6.1 sklearn实现决策树介绍
优点:
- 数据量需求少,可以不规范,但是不能有缺失值;
- 花费为训练数据点个数的对数;
- 白盒模型,可以看得到决策过程;
- 可用统计数据验证模型。
缺点:
- 容易过拟合;
- 不稳定,对某些类别主导地位的样本有偏见,要平衡样本的分类集合;
使用建议:
- 特征较多时,需要足够的样本来训练;
- 样本少,特征多情况下,需要对特征进行维度规约,减少一定的特征数量;
- 注意类别平衡;
- 决策树的数组使用的是numpy的float32类型,如果训练数据不是这样的格式,算法会先做copy再运行。
6.2 对泰坦尼克号生存人员特征分析
系统:windows 10
python版本:python3.8.1
编译器:jupyter notebook
# 1、数据获取
import pandas as pd
titanic = pd.read_csv('./data/titanic.csv')# 这里获取的是泰坦尼克号上生存人数与其他特征的关系
X = titanic[['pclass','age','sex']]
y = titanic['survived']
print(X.shape)
print(y.shape)
# 2、数据预处理:训练集测试集分割,标准化
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction import DictVectorizer # 特征转换器
X['age'].fillna(X['age'].mean(), inplace=True) # 用平均年龄对空值进行填充
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.25,random_state=33)# 数据划分
vec = DictVectorizer(sparse=False)# 对离散变量中的值分别编号为0/1,连续变量不变
X_train = vec.fit_transform(X_train.to_dict(orient='record'))
X_test = vec.transform(X_test.to_dict(orient='record'))
print(vec.feature_names_) # 输出特征名字
print(vec.vocabulary_) # 输出特征编码
print(X_train[:5,:]) # 输出训练集前五行
# 3、使用决策树对测试数据进行类别预测
from sklearn.tree import DecisionTreeClassifier
dtc = DecisionTreeClassifier()
dtc.fit(X_train,y_train) # 通过决策树分类器对训练集进行学习
y_predict = dtc.predict(X_test) # 用学习的
y_predict
# 4、获取结果报告
from sklearn.metrics import classification_report
print("Accracy:", dtc.score(X_test,y_test))
print(classification_report(y_predict, y_test, target_names=['died','survived']))
# 5、将生成的决策树保存,并画出来
from sklearn import tree
with open('DecisionTree.dot', 'w') as f:
f = tree.export_graphviz(dtc, out_file=f)
tree.plot_tree(dtc)
6.3 决策树图像显示
出于在jupyter notebook上使用sklearn.tree.plot_tree(dtc)函数画出来的函数出现模糊等问题,这里推荐使用graphviz软件进行决策树图形的输出,graphviz安装及基本使用参考windows下Graphviz安装及入门教程。
我们这里在6.2第5步中通过sklearn.tree.export_graphviz(dtc, out_filt=‘DecisionTree.dot’)来导出画图需要的dot文件,然后在DecisionTree.dot文件所在的文件目录下通过命令行,使用命令dot -T pdf DecisionTree.dot -o DT.pdf,生成DT.pdf文件,在pdf文件中对决策树的信息能通过缩放清晰的显示,其决策树图形如下所示:
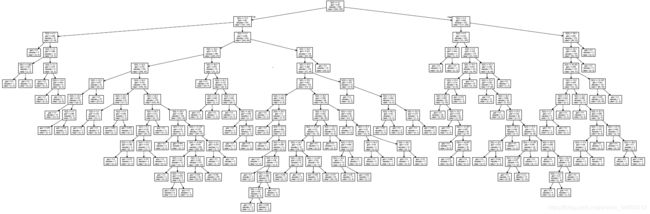
附数据和graphviz windows安装包:
链接:https://pan.baidu.com/s/1qVDiH2LfzHIMEAtvd-tgNA
提取码:li31
本博文供交流学习所用,参考了大量的博文和书本。
参考
[1] 《统计学习方法》 李航著
[2] 《机器学习》 周志华著
[3] 自编代码实现 https://github.com/fengdu78/lihang-code
[4] [python机器学习及实践(4)] Sklearn实现决策树并用Graphviz可视化决策树 https://www.cnblogs.com/youngsea/p/9330229.html
[5] sklearn实现决策树 https://blog.csdn.net/weixin_39667003/article/details/85198125
[6] windows下Graphviz安装及入门教程 https://www.cnblogs.com/onemorepoint/p/8310996.html