数据挖掘-理论与算法(公开课笔记一)
目录
- 2 Data Preprocessing 数据预处理
- 2.1.1 Data Cleaning 数据清洗
- 2.2.1 Outliers & Duplicate detection 异常值与重复检测
- 2.3.1 Type conversion & sampling 类型转换与采样
- 2.4.1 Data Description & Visualization 数据描述与可视化
- 2.5.1 Feature Selection 特征选择
- 2.6.1 Feature Extraction 特征提取
- 2.7.1 Linear Discriminant Analysis 线性判别分析
- 2.7.2 LDA Example 线性判别分析例子
- 3 Bayes & Decision Tree Classifiers 贝叶斯和决策树
- 3.1.1 Bayes、Decision Tree 贝叶斯、决策树(概率基础)
- 3.2.1 Naive Bayes Classifier 朴素贝叶斯公式
- 3.3.1 Decision Tree 决策树
- 3.4.1 Decision Tree Framework 决策树的建立策略
- 4 Neural Networks 神经网络
- 4.1.1 Perceptrons 感知机
- 4.2.1 感知机的应用
- 4.3.1 Multilayer Perception 多层感知机神经网络
- 4.4.1 分类器学习算法
- 4.5.1 Beyond BP Networks 其他的神经网络算法
- 5 Support Vector Machines 支持向量机
- 5.1.1 Support Vector Machine(SVM) 支持向量机
- 5.2.1 Linear SVM 线性SVM
- 5.3.1 Non-linear SVM 非线性SVM
2 Data Preprocessing 数据预处理
2.1.1 Data Cleaning 数据清洗
获取的数据可能不可用,存在缺数据、数据错误、噪音等问题,这些都会导致程序无法运行。因此在处理之前要进行清洗等操作。
对于缺失少量的数据,可以进行适当的推测,或者规则界定,或者直接填均值,这个处理方法主要依经验判断。 More art than science.
离群点和异常点是有区别的,要谨慎的区分两者。(如姚明身高可以称为离群点,但不是异常点)
2.2.1 Outliers & Duplicate detection 异常值与重复检测
异常是相对的,在计算异常值时要考虑相对性,可以尝试与近邻值相比较。
相同的信息可以用不同的形式来表示,而计算机可能无法识别这些重复。
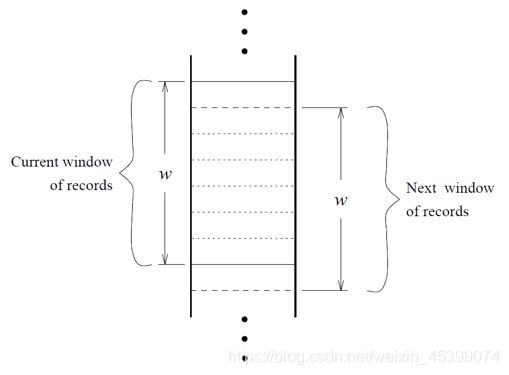
我们可以尝试使用滑动窗口,将某数据与部分之前的数据进行比(前提是相似的数据是紧邻的)
2.3.1 Type conversion & sampling 类型转换与采样
数据有很多形式,在编码时需要选择合适的方式进行处理,才能进行数据挖掘。在编码时,编码不同方式对问题结构和挖掘结果都会产生影响。
采样:数据并不是都需要的,而且IO操作对数据库并不友好,我们可以根据需要可以进行适当的采样,能有效的降低数据量,加快处理速度。
不平衡的数据集对挖掘结果也会有影响,在采样时也需要谨慎选择(可以尝试“复制”一些较少点加入数据集)。在做分类的情况下,当数据过多时,也可以尝试识别出边缘点并进行加入数实验据集,可以有效地降低实验时的数据量;当某一类别的数据过少,可以多采集一点,或生成一些邻近的点。如:

2.4.1 Data Description & Visualization 数据描述与可视化
数据标准化
2.5.1 Feature Selection 特征选择
在做数据挖掘的时候,要在多个属性中进行挑选,否则会影响算法的效率与资源的消耗,所以属性需要分好坏。
熵-(Entropy):在数据挖掘中,代表变量/系统的不确定性。

此处b一般取2,但也可以为其他值,取2时单位为比特;b取e时,单位为纳特。
信息增益-(information gain):在数据挖掘中代表属性的价值。
ΔH(x)=H(x1)−H(x2)ΔH(x) ,即增加属性前后熵的差值。
属性组的优劣并不是单纯的单个属性好坏的叠加,因为属性间可能有影响或者关联。
搜索最优属性-(Subset Seach):为了在众多属性中挑选最优的属性组,会有众多的排列组合,所以需要通过适当的算法。
Branch and Bound:寻找最优的属性组。建立属性树,如有单调的情况,可以通过剪枝方法加速。启发式、模拟退火等算法同样适用。
2.6.1 Feature Extraction 特征提取
引例:照片把三维信息压缩(投影)为二维,信息损失很多,人们通过照片的特征,依旧可以识别照片中的物体。
不同的属性有不同的区分度,越重要的属性越能区分物体,更少产生重复。所以属性有好坏。
主成分分析技术-PCA(principle components analysis):把空间中的点投影到空间中的一根线上(相当于n维降到1维),相当于降维,投影方向(相当于属性)有好坏。最优情况为最大特征向量。另外,投影后实际上相当于丢失了一部分信息。
2.7.1 Linear Discriminant Analysis 线性判别分析
PCA是一种无监督学习,虽然可以进行降维,但是在分类时,PCA可能无法进行合理的投影方向选择,导致无法进行分类。
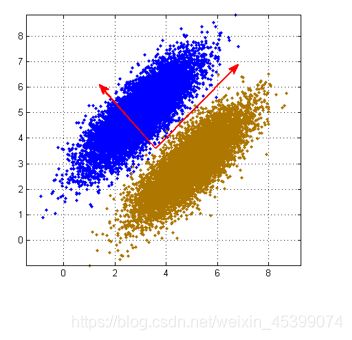
举例:如果向1轴投影,可以明显区分两个数据集,但是PCA会向2轴投影,导致两个数据在低维混合,看不出分类。
线性判别分析-LDA(Liner Discriminant Analysis):相对PCA,LDA在投影的同时保留类的区分信息(指相同组中数据尽可能近,不同组中数据尽可能远)
费舍尔准则-(Fisher Criterion):用于评估投影效果好坏(整体上J越大越好)
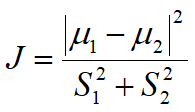
其中μ为组中心点位置(越远越好),S为各组离散程度(越小越好)。
调整投影方向,J值变化。

2.7.2 LDA Example 线性判别分析例子
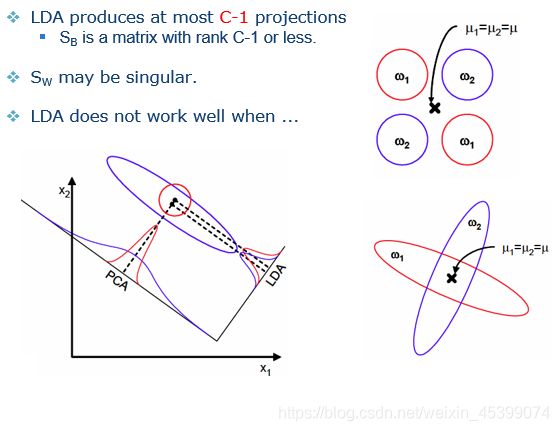
PCA与LDA的结果不一定相同。

LDA不局限于二分类,可以容易的拓展到n类的情况,此时J的分子为各个组中心点离所有点中心点的距离。此时n分类最高可以投影到n−1维上。如下,是三类问题投影到两个轴上(这两个轴不一定正交)。
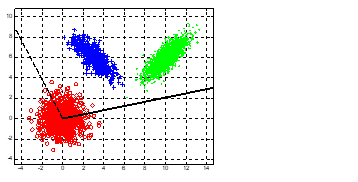
往两个轴投影如下:
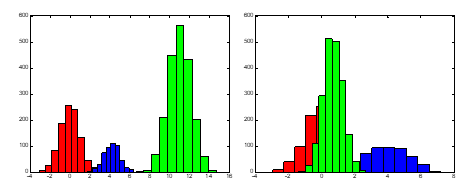
在一些特殊情况下(两类比较近μ1=μ2或者两个分类维互相垂直),LDA的分类可能不如PCA,在使用时要谨慎分析。
3 Bayes & Decision Tree Classifiers 贝叶斯和决策树
3.1.1 Bayes、Decision Tree 贝叶斯、决策树(概率基础)
分类是一种有监督学习,会有标签,这也是分类与聚类的差别。
3.2.1 Naive Bayes Classifier 朴素贝叶斯公式
注意区分:先验后验、相关独立。
拉普拉斯平滑-(Laplace Smoothing):如果出现数据库中从未存储的特殊点,一项为0会导致整个概率公式值为0。
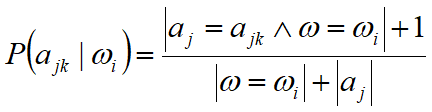
(加1使得结果不会为0)
贝叶斯公式的实际应用:
我们可以提取文章中的部分单词,根据出现与否计算文章分类概率,但是这种情况会导致计算量非常大。进一步改进,词袋模型-(Word Bag),不考虑单词出现的位置,根据单词在文章中出现的频率来计算文章分类概率。
3.3.1 Decision Tree 决策树
将不同因素设定规则,分层计算,形成决策树。决策树是可解释的(if…then…),是决策树的一大优势。
根据判断顺序不同,一个数据集可以建立很多树。运用奥卡姆剃刀,我们可以选择同样分类效率下,尽量简单的决策树。
3.4.1 Decision Tree Framework 决策树的建立策略
把分类能力强的节点放在靠近根节点的情况可以大大缩小树的规模,于是决策树的建立与属性判断有关。
熵-(Entropy):在变量选择中,代表属性的不确定性。最大值为1,此时最不确定。最小值为0,此时最确定。
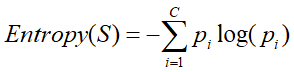
此处b一般取2,但也可以为其他值,取2时单位为比特。
过学习-(Overfitting):在训练集中a比b效果好,但在测试集中b比a好,此时就发生了过学习(通用概念)
决策树并不是越大越好,也存在过学习(overfitting)的情况。为避免过学习,提高泛化能力,有两种剪枝策略:
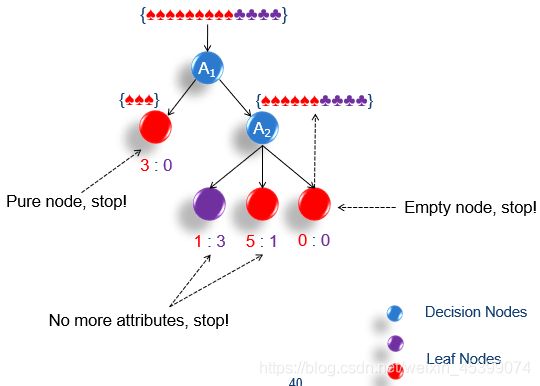
简单的决策树 ID3 建立过程:
- 寻找能把数据集分的最开的属性,进行分割
- 如果子集纯,那么停止分割,如果不纯,继续从1分割(如果没有属性,停止分割,标签少数服从多数)
4 Neural Networks 神经网络
4.1.1 Perceptrons 感知机
神经网络是计算机程序对大脑中神经元的简化抽象模拟。
单个神经元开关速度(0,1互换)相对计算机比较慢,但人脑是多个神经元联合分布式处理的,处理速度很快。
感知机-(Perceptrons):单个的神经元,n个输入,n+1个权重(w0,避免所有点都过原点),输出0或1。
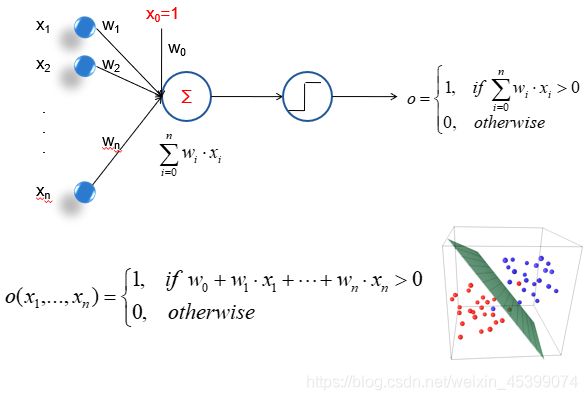
4.2.1 感知机的应用
感知机可以理解为一个线性分类器,对于线性不可分等问题无能为力。
梯度下降法-(Gradient Descent):取权重时不同权重对结果影响不同,所以让误差不断梯度下降。
批处理学习-(Batch Learning):计算一批数据,将更改值保存在Δw中,计算完后统一修改w。
随机学习-(Stochastic Learning):一旦出现误差,就修改w。
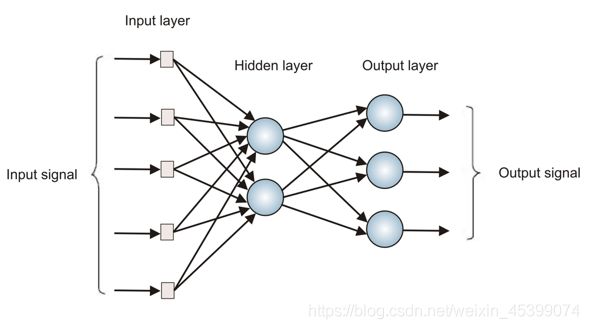
4.3.1 Multilayer Perception 多层感知机神经网络
多层感知机通过在输入和输出间添加隐含层来解决线性不可分的问题,提升效率。
多次感知机解决线性不可分问题:将输入的线性不可分问题转化为线性可分问题,输出到隐层,由隐含层解决并输出。
4.4.1 分类器学习算法
误差反向传播算法-BP(Backpropagation Rule):思想类似于感知机,用误差对某个权重的输入求偏导。但在多层感知机网络中,由于隐含层的期望值并不知道,所以没法得知隐含层的误差,因此输出后根据结果加权反向反馈,修改参数。
在求导时,很容易使参数掉进局部最优点,导致误差不在下降,而神经网络恰恰有很多局部最优点。为了解决这个问题,
- 我们可以尝试多次从不同点、不同方向出发,寻找最优参数。
- 也可以增加“冲量”,相当于“惯性”,让参数点冲过一些比较小的局部最优点。
- 也可以尝试改变学习率,较大的学习率可以直接大踏步跳过一些比较小的局部点,
- 而特殊的学习率会在一些特殊情况产生震荡,左右横跳导致无法收敛,多次学习也是解决办法。
↑↑↑可以结合小球滚斜坡、走路上下坡理解局部最优点↑↑↑
同样,神经网络也有过学习问题。所以我们既要设置训练误差-(Training Error)—–随时间逐步降低,又要设置校验误差-(Validation Error)—–随时加先降后升。在校验误差拐点停止训练即可。
4.5.1 Beyond BP Networks 其他的神经网络算法
Elman Network:此算法有一定的记忆性,通过之前的输入推出答案,输出不仅仅取决于当前的输入,还取决于之前的输入。
Hopfield Network:是一个全连接神经网络。类似于人大脑的记忆功能,利用收敛到局部最小值,实现联想记忆。
同样,不存在万能的神经网络,每个网络算法都有自己的适应性,而且神经网络的训练时间很长,但训练完成后反应很快。
神经网络的可解释性很差(只有权重)。
5 Support Vector Machines 支持向量机
5.1.1 Support Vector Machine(SVM) 支持向量机
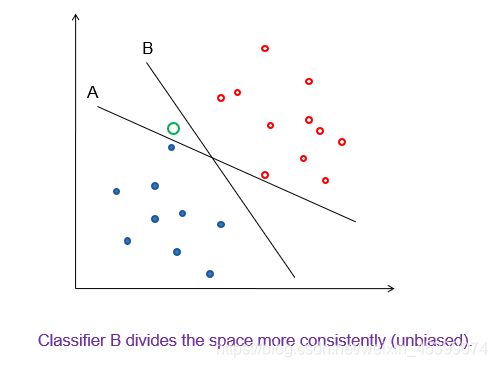
原理:输入维度向高维映射并进行分类(升维),仍然是线性分类器的一种,真正有效的点只有support vector,最大化margin。

B和A相比,把点分得更均匀,无偏。
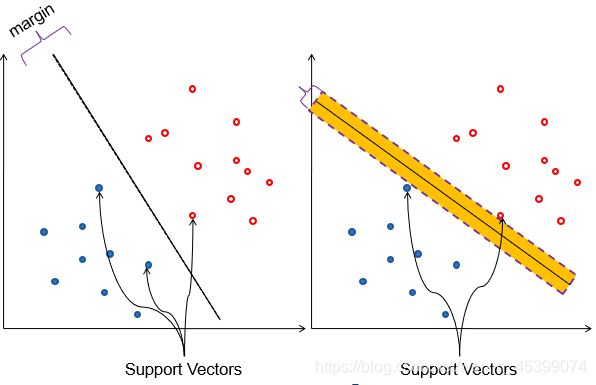
边缘-(margin):训练集中分界面可以上下平移的区域,margin越大,错误越不会影响结果,参数越好。
支持点-(Support Vectors):导致平移边界的点,决定了分界面能移动的范围。其他的点对分界没有影响,可忽略。
5.2.1 Linear SVM 线性SVM
目标:先分样本(必须分对所有的点),再求最优值
数学工具:拉格朗日乘数法
但事实上很难完美的分对所有点,所以放宽条件(soft margin),允许少数点可以不满足约束条件。
本质上还是一个线性分类器,仍然无法解决线性不可分问题。(soft margin只能解决数据有噪点的情况)
5.3.1 Non-linear SVM 非线性SVM
目的:弥补线性SVM不能解决线性不可分问题的缺陷。
原理:输入坐标点向新坐标空间映射并进行分类,可以是升维,也可以是同维度转化。如下图,第一个线性可分,但第二个线性不可分,则将第二个映射到新的空间。

映射的结果并不唯一,如下图。


映射方法一般是固定的,m维一般升到 m2/2 维进行分类。
通过引入核函数(Kernel Function) 进行等价变换,让高维空间的计算等价于低维空间的运算,有效降低运算量。
在处理文本数据时,可以使用字符串核函数,处理字符串的子串,得到相应的式子进行分类。
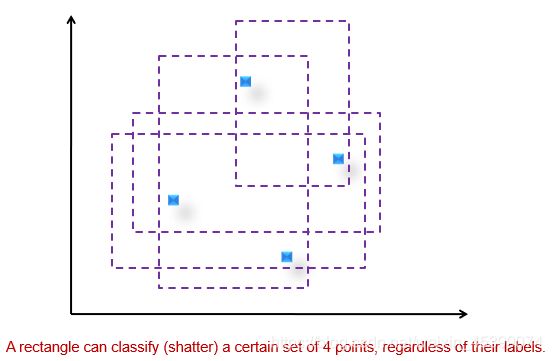
模型能力指数(model capacity):若h个点无论怎么打标签,模型都能区分(shatter),那么该模型能力指数就是h。