机器学习之房价预测
本文所述内容,参考了机器学习实战:基于
Scikit-Learn和TensorFlow一书。
修正了书籍中的代码错误,文章中代码从上到下,组成一个完整的可运行的项目。
框架问题
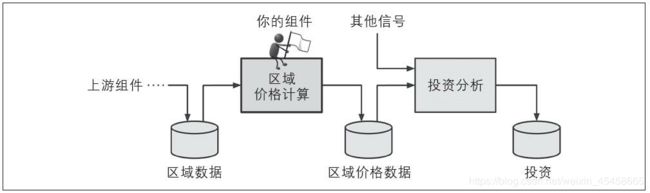
数据流水线:一个序列数据处理组件称为一个数据流水线,组件通常是异步运行,组件和组件之间的连接只有数据仓库。
-
选择性能指标
在回归问题中,经常使用均方根误差(RMSE)来衡量,它是预测错误的标准差,公式如下:
R M S E ( X , h ) = 1 m ∑ i = 1 m ( h ( x ( i ) − y ( i ) ) 2 {\rm{RMSE}}(X,h) = \sqrt {{1 \over m}\sum\limits_{i = 1}^m {(h({x^{(i)}}} - {y^{(i)}}{)^2}} RMSE(X,h)=m1i=1∑m(h(x(i)−y(i))2当有很多离群区域时,可以使用平均绝对误差。公式如下:
M A E ( X , h ) = 1 m ∑ i = 1 m ∣ ( h ( x ( i ) − y ( i ) ) ∣ {\rm{MAE}}(X,h) = {1 \over m}\sum\limits_{i = 1}^m {|(h({x^{(i)}}} - {y^{(i)}})| MAE(X,h)=m1i=1∑m∣(h(x(i)−y(i))∣
方根误差和平均误差都是测量两个向量的距离:预测向量和目标值向量。距离或者范数的测度:- 计算平方根的和(RMSE)对应欧几里得范数:l2范数。
- 计算绝对值的总和(MAE)对应l1范数。
包含n个元素Vk的范数可以定义为:
∣ ∣ V k ∣ ∣ = ( ∣ v 0 ∣ k + ∣ v 1 ∣ k + . . . + ∣ v n ∣ k ) 1 k . l 0 ||{V_k}|| = {(|{v_0}{|^k} + |{v_1}{|^k} + ... + |{v_n}{|^k})^{{1 \over k}}}.{l_0} ∣∣Vk∣∣=(∣v0∣k+∣v1∣k+...+∣vn∣k)k1.l0
l0给出了向量基数,loo给出了向量中的最大绝对值。范数指数越高,越关注大的价值,RMSE比MAE对异常值更敏感。
提供给机器 学习系统的信息称为信号,需要提高信噪比。
对于正态分布:大约68%的值落在1σ内,95%落
在2σ内,99.7%落在3σ内。
获取数据
使用pip安装以下库:Jupyter、Pandas、NumPy、 Matplotlib以及Scikit-Learn。
下载数据集:
import os
import tarfile
from six.moves import urllib
download_root = "https://raw.githubusercontent.com/ageron/handson-ml/master/"
housing_path = "dataset/housing"
housing_url = download_root + housing_path + "/housing.tgz"
def fetch_housing_data(housing_url=housing_url, housing_path=housing_path):
if not os.path.isdir(housing_path):
os.makedirs(housing_path)
tgz_path = os.path.join(housing_path, "housing.tgz")
# 需要魔法才能访问,可以先下载
if not os.path.exists(tgz_path):
urllib.request.urlretrieve(housing_url, tgz_path)
housing_tgz = tarfile.open(tgz_path)
housing_tgz.extractall(path=housing_path)
housing_tgz.close()
解压后的数据文件是CSV文件格式,可以使用pandas加载数据:
import pandas as pd
def load_housing_data(housing_path=housing_path):
csv_path = os.path.join(housing_path, "housing.csv")
return pd.read_csv(csv_path)
housing = load_housing_data(housing_path)
housing.head()
housing.info() # 快速获取数据集的简单描述
###
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 10 columns):
longitude 20640 non-null float64
latitude 20640 non-null float64
housing_median_age 20640 non-null float64
total_rooms 20640 non-null float64
total_bedrooms 20433 non-null float64
population 20640 non-null float64
households 20640 non-null float64
median_income 20640 non-null float64
median_house_value 20640 non-null float64
ocean_proximity 20640 non-null object
dtypes: float64(9), object(1)
memory usage: 1.6+ MB
None
注意到total_bed这个属性只有20433,这意味着有207个区域缺失这个特征。
housing['ocean_proximity'].value_counts() # 查看分类
###
<1H OCEAN 9136
INLAND 6551
NEAR OCEAN 2658
NEAR BAY 2290
ISLAND 5
Name: ocean_proximity, dtype: int64
housing.describe(); # 查看数值属性
###
longitude latitude ... median_income median_house_value
count 20640.000000 20640.000000 ... 20640.000000 20640.000000
mean -119.569704 35.631861 ... 3.870671 206855.816909
std 2.003532 2.135952 ... 1.899822 115395.615874
min -124.350000 32.540000 ... 0.499900 14999.000000
25% -121.800000 33.930000 ... 2.563400 119600.000000
50% -118.490000 34.260000 ... 3.534800 179700.000000
75% -118.010000 37.710000 ... 4.743250 264725.000000
max -114.310000 41.950000 ... 15.000100 500001.000000
[8 rows x 9 columns]
25%、50%和75%行显示相应的百分位数:百分位数表示一组观测值中给定百分比的观测值都低于该值。
绘制数值属性直方图:
import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(20, 15))
plt.show()
创建测试集
创建测试集最简单的方法
import numpy as np
def split_train_test(data, test_ratio):
shuffled_indices = np.random.permutation(len(data))
test_set_size = int(len(data) * test_ratio)
test_indices = shuffled_indices[:test_set_size]
train_indices = shuffled_indices[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]
train_set, test_set = split_train_test(housing, 0.2)
print(len(train_set), "train +", len(test_set), "test")
###
16512 train + 4128 test
但是上述代码在多次运行时会返回不同的结果,为了保持一致,可以在第一次运行后保存测试集或者使用相同的随机种子生成相同的索引。常用的方法时为每个实例创建唯一的标识符,如使用行索引:
def test_set_check(identifier, test_radio, hash):
return hash(np.int64(identifier)).digest()[-1] < 256 * test_radio # 取最后一个字节判断
def split_train_test_by_id(data, test_ratio, id_column, hash=hashlib.md5):
ids = data[id_column]
in_test_set = ids.apply(lambda id_: test_set_check(id_, test_ratio, hash))
return data.loc[~in_test_set], data.loc[in_test_set]
housing_with_id = housing.reset_index() # index
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "index")
print(len(train_set), "train +", len(test_set), "test")
也可以使用稳定的特征来创建标识符:
housing_with_id["id"]=housing["longitude"]*1000+housing["latitude"]
train_set, test_set = split_train_test_by_id(housing_with_id,0.2,"id")
使用scikit-learn内置函数来实现分割子集:
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
在数据集足够大的情况下,可以使用纯随机抽样的方法,否则应考虑分层抽样。如将收入的中位数除以1.5(限制收入类别数量),然后使用ceil进行取整,最后将所有大于5的类别合并为5:
import numpy as np
housing["income_cat"] = np.ceil(housing["median_income"] / 1.5)
housing["income_cat"].where(housing["income_cat"] < 5, 5.0, inplace=True) # 小于号
进行分层抽样:
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(housing, housing["income_cat"]):
strat_train_set = housing.loc[train_index]
strat_test_set = housing.loc[test_index]
housing["income_cat"].value_counts()/len(housing)
###
3.0 0.350581
2.0 0.318847
4.0 0.176308
5.0 0.114438
1.0 0.039826
Name: income_cat, dtype: float64
删除income_cat属性,使数据恢复原样:
for set1 in (strat_test_set, strat_train_set):
set1.drop(["income_cat"], axis=1, inplace=True)
数据可视化
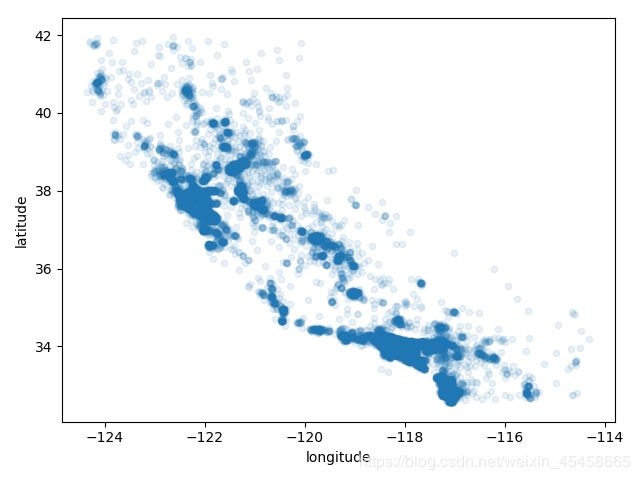
housing = strat_train_set.copy()
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1) # 颜色浅表示密度小
plt.show()
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
s=housing["population"] / 100, label="population",
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True)
plt.legend()
- 寻找相关性
皮尔逊相关系数(标准相关系数):相关系数的范围从-1变化到1。越接近1,表示有越强的正相关,当系数接近
于-1,则表示有强烈的负相关,系数靠近0则说明二者之间没有线性相关性。
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)
###
median_house_value 1.000000
median_income 0.687160
total_rooms 0.135097
housing_median_age 0.114110
households 0.064506
total_bedrooms 0.047689
population -0.026920
longitude -0.047432
latitude -0.142724
Name: median_house_value, dtype: float64
使用Pandas的scatter_matrix检测属性相关性:
from pandas.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms",
"housing_median_age"]
scatter_matrix(housing[attributes], figsize=(12, 8))
plt.show()
 可以看到收入中位数和房价中位数相关数很强。但其中有一些支线,这些地区需要删除。
可以看到收入中位数和房价中位数相关数很强。但其中有一些支线,这些地区需要删除。
- 试验不同属性组合
housing["rooms_per_household"] = housing["total_rooms"] / housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"] / housing["total_rooms"]
housing["population_per_household"] = housing["population"] / housing["households"]
# 查看关联矩阵
corr_matrix = housing.corr()
print(corr_matrix["median_house_value"].sort_values(ascending=False))
###
16362 train + 4278 test
median_house_value 1.000000
median_income 0.688075
rooms_per_household 0.151948
total_rooms 0.134153
housing_median_age 0.105623
households 0.065843
total_bedrooms 0.049686
population_per_household -0.023737
population -0.024650
longitude -0.045967
latitude -0.144160
bedrooms_per_room -0.255880
Name: median_house_value, dtype: float64
数据准备
将预测器和标签分开:
housing=strat_train_set.drop("median_house_value",axis=1) # 创建新的副本
housing_labels=strat_train_set["median_house_value"]
- 数据清理
注意到total_bedrooms属性有部分值缺失:放弃这些相应地区,放弃这个属性或将缺失值设置为某个值(0,平均数,或中位数)。
housing.dropna(subset=["total_bedrooms"]) # 1
housing.drop("total_bedrooms",axis=1) #2
median=housing["total_bedrooms"].median()
housing["total_bedrooms"].fillna(median) #3
使用scikit-learn来处理:
from sklearn.impute import SimpleImputer
imputer=SimpleImputer(strategy="median") # 中位数
housing_num=housing.drop("ocean_proximity",axis=1) # 数据副本,剔除文本属性
imputer.fit(housing_num)
print(imputer.statistics_)
print(housing_num.median().values)
X=imputer.transform(housing_num) # 替换缺失值
housing_tr=pd.DataFrame(X,columns=housing_num.columns) # 放回
- 处理文本属性和分类属性
将文本标签转换为数字:
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
housing_cat = housing["ocean_proximity"]
housing_cat_encoded = encoder.fit_transform(housing_cat)
print(housing_cat_encoded) # [0 0 4 ... 1 0 3]
print(encoder.classes_) # ['<1H OCEAN' 'INLAND' 'ISLAND' 'NEAR BAY' 'NEAR OCEAN']依次对应0,1,......
由于机器学习算法会以为两个相近放入数字比离得远的数字会更相近一些,上述算法会带来问题。最好使用独热编码。
from sklearn.preprocessing import OneHotEncoder
encoder=OneHotEncoder()
housing_cat_1hot=encoder.fit_transform(housing_cat_encoded.reshape(-1,1))
print(housing_cat_1hot.toarray())
###
[[1. 0. 0. 0. 0.]
[1. 0. 0. 0. 0.]
[0. 0. 0. 0. 1.]
...
[0. 1. 0. 0. 0.]
[1. 0. 0. 0. 0.]
[0. 0. 0. 1. 0.]]
使用LabelBinarizer一次性完成两个转换:
from sklearn.preprocessing import LabelBinarizer
encoder=LabelBinarizer() # sparse_output=True 输出为稀疏矩阵
housing_cat_1hot=encoder.fit_transform(housing_cat)
print(housing_cat_1hot)
- 自定义转换器
要与Scikit-Learn自身功能相连接,只需要实现fit()(返回自身)、transform()、fit_transform()三个方法即可,添加TransformerMixin作为基类,就可以直接得到最后一个方
法。如果添加BaseEstimator作为基类(并在构造函数中避免*args和**kargs),还能额外获得两个非常有用的自动调整超参数的方法(get_params()和set_params())。
from sklearn.base import BaseEstimator, TransformerMixin
room_ix, bedrooms_ix, population_ix, household_ix = 3, 4, 5, 6
class CombinedAttributesAdder(BaseEstimator, TransformerMixin):
def __init__(self, add_bedrooms_per_room=True):
self.add_bedroom_per_room = add_bedrooms_per_room
def fit(self, x, y=None):
return self
def transform(self, x, y=None):
rooms_per_household = x[:, room_ix] / x[:, household_ix]
population_per_household = x[:, population_ix] / x[:, household_ix]
if self.add_bedroom_per_room:
bedrooms_per_room = x[:, bedrooms_ix] / x[:, household_ix]
return np.c_[x, rooms_per_household, population_per_household, bedrooms_per_room]
else:
return np.c_[x, rooms_per_household, population_per_household]
attr_adder = CombinedAttributesAdder(add_bedrooms_per_room=False)
housing_extra_attribs = attr_adder.transform(housing.values)
- 特征缩放
同比例缩放所有属性,常用的两种方法是:最小-最大缩放和标准化。
最小-最大缩放(又叫作归一化):将值重新缩放使其最终范围归于0到1之间。实现方法是将值减去最小值并除以最大值和最小值的差。
标准化:首先减去平均值(所以标准化值的均值总是零),然后除以方差,从而使得结果的分布具备单位方差。
一个完整的处理数值和分类属性的流水线:
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.pipeline import FeatureUnion, Pipeline
class DataFrameSelector(BaseEstimator, TransformerMixin): # 属性选择
def __init__(self, attribute_names):
self.attribute_names = attribute_names
def fit(self, x, y=None):
return self
def transform(self, x, y=None):
return x[self.attribute_names].values
class MyLabelBinarizer(TransformerMixin): # 自定义文本转换
def __init__(self, *args, **kwargs):
self.encoder = LabelBinarizer(*args, **kwargs)
def fit(self, x, y=None):
self.encoder.fit(x)
return self
def transform(self, x, y=None):
return self.encoder.transform(x)
num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]
num_pipeline = Pipeline([
('selector', DataFrameSelector(num_attribs)),
('imputer', SimpleImputer(strategy="median")),
("attribs_adder", CombinedAttributesAdder()),
('std_scaler', StandardScaler()),
])
cat_pipeline = Pipeline([
('selector', DataFrameSelector(cat_attribs)),
('label_binarizer', MyLabelBinarizer()),
])
full_pipeline = FeatureUnion(transformer_list=[
('num_pipeline', num_pipeline),
('cat_pipeline', cat_pipeline),
])
housing = strat_train_set.copy()
housing_prepared = full_pipeline.fit_transform(housing)
print(housing_prepared)
###
[[-1.15604281 0.77194962 0.74333089 ... 0. 0.
0. ]
[-1.17602483 0.6596948 -1.1653172 ... 0. 0.
0. ]
[ 1.18684903 -1.34218285 0.18664186 ... 0. 0.
1. ]
...
[ 1.58648943 -0.72478134 -1.56295222 ... 0. 0.
0. ]
[ 0.78221312 -0.85106801 0.18664186 ... 0. 0.
0. ]
[-1.43579109 0.99645926 1.85670895 ... 0. 1.
0. ]]
选择和训练模型
- 选择线性模型
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lin_reg=LinearRegression()
lin_reg.fit(housing_prepared,housing_labels)
housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels, housing_predictions)
lin_rmse = np.sqrt(lin_mse)
print(lin_rmse) #68911.49637588045
some_data=housing.iloc[:5]
some_labels=housing_labels.iloc[:5]
some_data_prepared=full_pipeline.transform(some_data)
print("Predictions:\t", lin_reg.predict(some_data_prepared))
#Predictions: [211881.21811279 321219.24211009 210877.63065012 62198.25451316 194847.8414579 ]
print("Labels:\t\t", list(some_labels))
#Labels: [286600.0, 340600.0, 196900.0, 46300.0, 254500.0]
很显然是由于拟合不足,使用DecisionTreeRegressor来试试:
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor()
tree_reg.fit(housing_prepared, housing_labels)
housing_predictions = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_predictions)
print(np.sqrt(tree_mse)) #0.0
损失为0可能是过拟合了,使用交叉验证来评估模型,下面使用K-折交叉验证: 将训练集随机分割成10个不同子集,每个子集称为一个折叠,然后对决策树进行10次训练和评估,每次使用一个折叠用于评估,其他9个用于训练。
from sklearn.model_selection import cross_val_score
score=cross_val_score(tree_reg,housing_prepared,housing_labels,scoring="neg_mean_squared_error",cv=10)
rmse_score=np.sqrt(-score)
# [71467.90559873 66303.44952599 71505.04870277 71591.20525551
# 69862.90187959 75183.61451558 73370.57154879 70353.75161801
#77883.8493838 69958.12755456] 更糟糕了!
使用RandomForestRegressor
from sklearn.ensemble import RandomForestRegressor
forest_reg=RandomForestRegressor()
forest_reg.fit(housing_prepared,housing_labels)
score=cross_val_score(forest_reg,housing_prepared,housing_labels,scoring='neg_mean_squared_error',cv=10)
forest_score=np.sqrt(-score)
###
[52235.20300676 50560.45476851 50994.46838252 54918.89963455
53060.19203137 55758.61740077 53267.63381615 51550.82465313
55777.15892869 52820.8176299 ]
保存训练过的模型:
from sklearn.externals import joblib
joblib.dump(forest_reg, "forest_reg.pkl")
forest_reg_loaded = joblib.load("forest_reg.pkl")
- 微调模型
- 网格搜索:使用
的GridSearchCV来交叉验证评估超参数的最优值。 - 随机搜索:使用
RandomizedSearchCV,在每次迭代中为超参数选择一个随机值,然后对一定数量的随机组合进行评估。 - 集成方法:将表现最优的模型组合起来。
- 网格搜索:使用
from sklearn.model_selection import GridSearchCV
param_grid=[
{'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]},
{'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]},
]
forest_reg=RandomForestRegressor()
grid_search=GridSearchCV(forest_reg,param_grid,cv=5, scoring='neg_mean_squared_error')
grid_search.fit(housing_prepared,housing_labels)
print(grid_search.best_params_) # {'max_features': 6, 'n_estimators': 30}
print(grid_search.best_estimator_)
print(grid_search.cv_results_)
- 分析最佳模型及其错误
feature_importances = grid_search.best_estimator_.feature_importances_
extra_attribs=["rooms_per_hhold","pop_per_hhold","bedrooms_per_room"]
cat_one_hot_attribs = list(encoder.classes_)
attributes = num_attribs + extra_attribs + cat_one_hot_attribs
print(sorted(zip(feature_importances, attributes), reverse=True))
###
[(0.3543354578587674, 'median_income'), (0.15977993470692203, 'INLAND'), (0.10403105662293761, 'pop_per_hhold'), (0.0.........
- 通过测试集评估系统
final_model=grid_search.best_estimator_
X_test=strat_test_set.drop("median_house_value",axis=1)
y_test=strat_test_set['median_house_value'].copy()
X_test_prepared=full_pipeline.transform(X_test)
final_predictions=final_model.predict(X_test_prepared)
final_mse=mean_squared_error(y_test,final_predictions)
final_rmse=np.sqrt(final_mse)
print(final_rmse) # 47682.10712356667
启动、监控和维护系统
在系统启动后编写监控代码,以定期检查系统的实时性能,同时在性能下降时触发警报。评估系统性能,需要对系统的预测结果进行抽样并评估,还需要评估输入系统的数据的质量。最后,使用新鲜数据定期训练你的模型。