【Python自然语言处理】中文分词技术——统计分词
中文分词方法
本文参考自书籍《Python自然语言处理实战:核心技术与算法》
用做个人的学习笔记和分享
1. 规则分词
规则分词的详细笔记
2. 统计分词
2.1 一般步骤
- 建立统计语言模型。
- 句子划分为单词,对划分结果进行概率分析,获得概率最大的分词方式。
- 常用统计学习算法:隐马尔可夫、条件随机场。
2.2 语言模型
语言模型的形式化描述:
长度为m的字符串的概率分布:
P ( w 1 , w 2 , . . . , w m ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 , w 2 ) . . . P ( w m ∣ w 1 , w 2 , . . . , w m − 1 ) (1) P(w_1,w_2,...,w_m)=P(w_1)P(w_2|w_1)P(w_3|w_1,w_2)...P(w_m|w_1,w_2,...,w_{m-1}) \tag{1} P(w1,w2,...,wm)=P(w1)P(w2∣w1)P(w3∣w1,w2)...P(wm∣w1,w2,...,wm−1)(1)
其中 w 1 w_1 w1到 w m w_m wm依次表示文本中的各个词语,采用链式法则计算概率值。
n-gram模型:文本过长,计算难度大,可忽略距离大于等于n的上文词的影响:
P ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) ≈ P ( w i ∣ w i − ( n − 1 ) , . . . , w i − 1 ) (2) P(w_i|w_1,w_2,...,w_{i-1})≈P(w_i|w_{i-(n-1)},...,w_{i-1}) \tag{2} P(wi∣w1,w2,...,wi−1)≈P(wi∣wi−(n−1),...,wi−1)(2)
一元模型:n=1,在一元语言模型中,整个句子的概率等于各个词语概率的乘积。言下之意就是各个词之间都是相互独立的,这无疑是完全损失了句中的词序信息。所以一元模型的效果并不理想:
P ( w 1 , w 2 , . . . , w m ) = P ( w 1 ) P ( w 2 ) . . . P ( w m ) (3) P(w_1,w_2,...,w_m)=P(w_1)P(w_2)...P(w_m) \tag{3} P(w1,w2,...,wm)=P(w1)P(w2)...P(wm)(3)
二元模型:n=2,式(2)变为:
P ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) ≈ P ( w i ∣ w i − 1 ) (4) P(w_i|w_1,w_2,...,w_{i-1})≈P(w_i|w_{i-1}) \tag{4} P(wi∣w1,w2,...,wi−1)≈P(wi∣wi−1)(4)
三元模型:n=3,式(2)变为:
P ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) ≈ P ( w i ∣ w i − 2 , w i − 1 ) (5) P(w_i|w_1,w_2,...,w_{i-1})≈P(w_i|w_{i-2},w_{i-1}) \tag{5} P(wi∣w1,w2,...,wi−1)≈P(wi∣wi−2,wi−1)(5)
当n≥2 时,该模型是可以保留一定的词序信息的,而且n 越大,保留的词序信息越丰富,但计算成本也呈指数级增长。
一般使用频率计数的比例来计算n 元条件概率,如式(6)所示:
P ( w i ∣ w i − ( n − 1 ) , . . . , w i − 1 ) = c o u n t ( w i − ( n − 1 ) , . . . , w i − 1 , w i ) c o u n t ( w i − ( n − 1 ) , . . . , w i − 1 ) (6) P(w_i|w_{i-(n-1)},...,w_{i-1}) = \frac{count(w_{i-(n-1),...,w_{i-1},w_i})}{count(w_{i-(n-1)},...,w_{i-1})} \tag{6} P(wi∣wi−(n−1),...,wi−1)=count(wi−(n−1),...,wi−1)count(wi−(n−1),...,wi−1,wi)(6)
当n越大时,模型包含的词序信息越丰富,同时计算量随之增大。与此同时,长度越长的文本序列出现的次数也会减少,如按照公式( 3.3 )估计n 元条件概率时,就会出现分子分母为零的情况。因此,一般在n 元模型中需要配合相应的平滑算法解决该问题,如拉普拉斯平滑算法等。
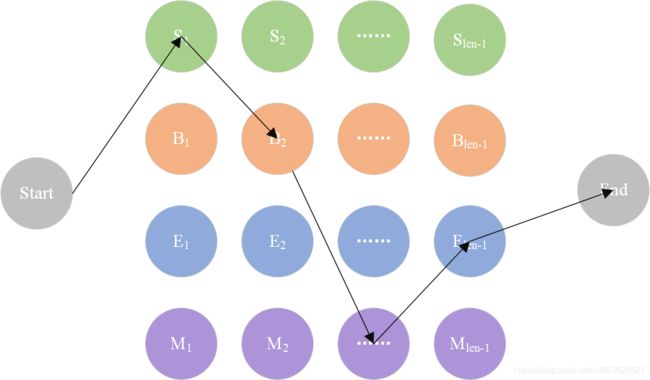
2.3 隐马尔可夫模型(HMM)
基本思路:每个字在构造一个特定的词语时都占据着一个确定的构词位置( 即词位),
现规定每个字最多只有四个构词位置:即B (词首)、M (词中)、E (词尾)和s (单独成词),那么下面句子①的分词结果就可以直接表示成如②所示的逐字标注形式:
①中文/文本处理/需要/进行/中文/分词/。
②中/B文/E文/B本/M处/M理/E需/B要/E/进/B行/E中/B文/E/分/B词/E。/S
形式化描述:
句子: λ = λ 1 λ 2 . . . λ n λ=λ_1λ_2...λ_n λ=λ1λ2...λn
标签: σ = σ 1 σ 2 . . . σ n σ=σ_1σ_2...σ_n σ=σ1σ2...σn
KaTeX parse error: \tag works only in display equations
其中 λ i λ_i λi是字,n为句长,σ∈{B,M,E,S}
P(σ|λ)是关于2n个变量的条件概率,n不固定,无法对P(σ|λ)进行精确计算,故引入观测独立性假设:每个字的输出仅与当前字有关。
P ( σ 1 σ 2 . . . σ n ∣ λ 1 λ 2 . . . λ n ) = P ( σ 1 ∣ λ 1 ) P ( σ 2 ∣ λ 2 ) . . . P ( σ n ∣ λ n ) (8) P(σ_1σ_2...σ_n|λ_1λ_2...λ_n) = P(σ_1|λ_1)P(σ_2|λ_2)...P(σ_n|λ_n) \tag{8} P(σ1σ2...σn∣λ1λ2...λn)=P(σ1∣λ1)P(σ2∣λ2)...P(σn∣λn)(8)
观察独立性假设存在的问题:完全没有考虑上下文,且会出现不合理的情况。比如按照之前设定的B 、M 、E 和S 标记,正常来说B后面只能是M或者E ,然而基于观测独立性假设,我们很可能得到诸如BBB 、BEM 等的输出,显然是不合理的。
HMM通过贝叶斯公式求解P(σ|λ)
P ( σ ∣ λ ) = P ( σ , λ ) P ( λ ) = P ( λ ∣ σ ) P ( σ ) P ( λ ) (9) P(σ|λ)=\frac{P(σ,λ)}{P(λ)}=\frac{P(λ|σ)P(σ)}{P(λ)} \tag{9} P(σ∣λ)=P(λ)P(σ,λ)=P(λ)P(λ∣σ)P(σ)(9)
λ为给定的输入,因此P(λ)计算为常数,可以忽略,因此最大化P(σ|λ)等价于最大
化P(λ|σ)P(σ)。
对P(λ|σ)P(σ)做马尔可夫假设:
P ( λ ∣ σ ) = P ( λ 1 ∣ σ 1 ) P ( λ 2 ∣ σ 2 ) . . . P ( λ n ∣ σ n ) (10) P(λ|σ)=P(λ_1|σ_1)P(λ_2|σ_2)...P(λ_n|σ_n) \tag{10} P(λ∣σ)=P(λ1∣σ1)P(λ2∣σ2)...P(λn∣σn)(10)
P ( σ ) = P ( σ 1 ) P ( σ 2 ∣ σ 1 ) P ( σ 3 ∣ σ 1 , σ 2 ) ⋅ ⋅ ⋅ P ( σ n ∣ σ 1 , σ 2 , … , σ n − 1 (11) P(σ) = P(σ_1)P(σ_2|σ_1)P(σ_3|σ_1,σ_2)···P(σ_n|σ_1,σ_2,…,σ_{n-1}\tag{11} P(σ)=P(σ1)P(σ2∣σ1)P(σ3∣σ1,σ2)⋅⋅⋅P(σn∣σ1,σ2,…,σn−1(11)
HMM做齐次马尔可夫假设:
P ( σ ) = P ( σ 1 ) P ( σ 2 ∣ σ 1 ) P ( σ 3 ∣ σ 2 ) . . . P ( σ n ∣ σ n − 1 ) (12) P(σ)=P(σ_1)P(σ_2|σ_1)P(σ_3|σ_2)...P(σ_n|σ_{n-1}) \tag{12} P(σ)=P(σ1)P(σ2∣σ1)P(σ3∣σ2)...P(σn∣σn−1)(12)
综上所述:
P ( λ ∣ σ ) P ( σ ) ~ P ( λ 1 ∣ σ 1 ) P ( σ 2 ∣ σ 1 ) P ( λ 2 ∣ σ 2 ) P ( σ 3 ∣ σ 2 ) . . . P ( σ n ∣ σ n − 1 ) P ( λ n ∣ σ n ) P(λ|σ)P(σ)~P(λ_1|σ_1)P(σ_2|σ_1)P(λ_2|σ_2)P(σ_3|σ_2)...P(σ_n|σ_{n-1})P(λ_n|σ_n) P(λ∣σ)P(σ)~P(λ1∣σ1)P(σ2∣σ1)P(λ2∣σ2)P(σ3∣σ2)...P(σn∣σn−1)P(λn∣σn)
其中 P ( λ k ∣ σ k ) P(λ_k|σ_k) P(λk∣σk)式发射概率, P ( σ k ∣ σ k − 1 ) P(σ_k|σ_{k-1}) P(σk∣σk−1)是转移概率,设置 P ( σ k ∣ σ k − 1 ) = 0 P(σ_k|σ_{k-1})=0 P(σk∣σk−1)=0可以排除BBB、EM等不合理的组合。
求解maxP(λ|σ)P(σ):常用Veterbi算法,算法效率 O ( n ∗ l 2 ) O(n*l^2) O(n∗l2),l为候选数目最多的节点 σ i σ_i σi的候选数目,与n成正比。
Veterbi算法:是一种动态规划方法,核心思想是:如果最终的最优路径经过某个 σ i σ_i σi,那么从初始节点到 σ i − 1 σ_{i-1} σi−1点的路径必然也是一个最优路径一一因为每一个节点 σ i σ_i σi只会影响前后两个 P ( σ i − 1 ∣ σ i ) P(σ_{i-1}|σ_{i}) P(σi−1∣σi)和 P ( σ i ∣ σ i + 1 ) P(σ_i|σ_{i+1}) P(σi∣σi+1)。
2.4 HMM的Python实现
- 定义HMM类,包含_init_方法、try_load_model方法、train方法
- init:初始化一些全局信息,用于初始化一些成员变量。如状态集合(标记
S 、B 、E 、M ),以及存取概率计算的中间文件。
def __init__(self):
import os
# 主要是用于存取算法中间结果,不用每次都训练模型
self.model_file = './data/hmm_model.pkl'
# 状态值集合
self.state_list = ['B', 'M', 'E', 'S']
# 参数加载,用于判断是否需要重新加载model_file
self.load_para = False
- try_load_model:接收一个参数,用于判别是否加载中间文件结果。当直接加载中间结果时,可以不通过语料库训练,直接进行分词调用。否则,该函数用于初始化初始概率、转移概率以及发射概率等。
# 用于加载已计算的中间结果,当需要重新训练时,需初始化清空结果
def try_load_model(self, trained):
if trained:
import pickle
with open(self.model_file, 'rb') as f:
self.A_dic = pickle.load(f)
self.B_dic = pickle.load(f)
self.Pi_dic = pickle.load(f)
self.load_para = True
else:
# 状态转移概率(状态->状态的条件概率)
self.A_dic = {}
# 发射概率(状态->词语的条件概率)
self.B_dic = {}
# 状态的初始概率
self.Pi_dic = {}
self.load_para = False
- train:主要用于通过给定的分词语料进行训练。语料的格式为每行一句话(这里以逗号隔开也算一句),每个词以空格分隔,这里采用了人民日报的分词语料。该函数主要通过对语料的统计, 得到HMM 所需的初始概率、转移概率以及发射概率。
# 计算转移概率、发射概率以及初始概率
def train(self, path):
# 重置几个概率矩阵
self.try_load_model(False)
# 统计状态出现次数,求p(o)
Count_dic = {}
# 初始化参数
def init_parameters():
for state in self.state_list:
self.A_dic[state] = {s: 0.0 for s in self.state_list}
self.Pi_dic[state] = 0.0
self.B_dic[state] = {}
Count_dic[state] = 0
def makeLabel(text):
out_text = []
if len(text) == 1:
out_text.append('S')
else:
out_text += ['B'] + ['M'] * (len(text) - 2) + ['E']
return out_text
init_parameters()
line_num = -1
# 观察者集合,主要是字以及标点等
words = set()
with open(path, encoding='utf8') as f:
for line in f:
line_num += 1
line = line.strip()
if not line:
continue
word_list = [i for i in line if i != ' ']
words |= set(word_list) # 更新字的集合
linelist = line.split()
line_state = []
for w in linelist:
line_state.extend(makeLabel(w))
assert len(word_list) == len(line_state)
for k, v in enumerate(line_state):
Count_dic[v] += 1
if k == 0:
self.Pi_dic[v] += 1 # 每个句子的第一个字的状态,用于计算初始状态概率
else:
self.A_dic[line_state[k - 1]][v] += 1 # 计算转移概率
self.B_dic[line_state[k]][word_list[k]] =\
self.B_dic[line_state[k]].get(word_list[k], 0) + 1.0 # 计算发射概率
self.Pi_dic = {k: v * 1.0 / line_num for k, v in self.Pi_dic.items()}
self.A_dic = {k: {k1: v1 / Count_dic[k] for k1, v1 in v.items()}
for k, v in self.A_dic.items()}
# 加1平滑
self.B_dic = {k: {k1: (v1 + 1) / Count_dic[k] for k1, v1 in v.items()}
for k, v in self.B_dic.items()}
# 序列化
import pickle
with open(self.model_file, 'wb') as f:
pickle.dump(self.A_dic, f)
pickle.dump(self.B_dic, f)
pickle.dump(self.Pi_dic, f)
return self
- veterbi方法:为Veterbi 算法的实现,是基于动态规划的一种实现,主要是求最大概率的路径。其输入参数为初始概率、转移概率以及发射概率,加上需要切分的句子。
def veterbi(self, text, states, start_p, trans_p, emit_p):
V = [{}]
path = {}
for y in states:
V[0][y] = start_p[y] * emit_p[y].get(text[0], 0)
path[y] = [y]
for t in range(1, len(text)):
V.append({})
newpath = {}
# 检验训练的发射概率矩阵中是否有该字
neverSeen = text[t] not in emit_p['S'].keys() and \
text[t] not in emit_p['M'].keys() and \
text[t] not in emit_p['E'].keys() and \
text[t] not in emit_p['B'].keys()
for y in states:
emitP = emit_p[y].get(text[t], 0) if not neverSeen else 1.0 # 设置未知字单独成词
(prob, state) = max(
[(V[t - 1][y0] * trans_p[y0].get(y, 0) *
emitP, y0)for y0 in states if V[t - 1][y0] > 0])
V[t][y] = prob
newpath[y] = path[state] + [y]
path = newpath
if emit_p['M'].get(text[-1], 0) > emit_p['S'].get(text[-1], 0):
(prob, state) = max([(V[len(text) - 1][y], y) for y in ('E', 'M')])
else:
(prob, state) = max([(V[len(text) - 1][y], y) for y in states])
return (prob, path[state])
- cut方法:用于分词,其通过加载中间文件,调用veterbi 函数来完成。
def cut(self, text):
import os
if not self.load_para:
self.try_load_model(os.path.exists(self.model_file))
prob, pos_list = self.viterbi(text, self.state_list, self.Pi_dic, self.A_dic, self.B_dic)
begin, next = 0, 0
for i, char in enumerate(text):
pos = pos_list[i]
if pos == 'B':
begin = i
elif pos == 'E':
yield text[begin: i + 1]
next = i + 1
elif pos == 'S':
yield char
next = i + 1
if next < len(text):
yield text[next:]
- 主函数
if __name__ == '__main__':
hmm = HMM()
hmm.train('./data/trainCorpus.txt_utf8')
text = '这是一个非常棒的方案!'
res = hmm.cut(text)
print(text)
print(str(list(res)))
# 分词结果:[’这是’, ’ 一个’, ’ 非常’, ’ 棒·, ’ 的’ , ’ 方案’ , ' !' l
2.5 其他统计分词算法
条件随机场CRF:基于马尔可夫思想的统计模型。在隐含马尔可夫中,有个很经典的假设,那就是每个状态只与它前面的状态有关。这样的假设显然是有偏差的,于是学者们提出了条件随机场算法,使得每个状态不止与他前面的状态有关,还与他后面的状态有关。
神经网络分词算法:深度学习方法在NLP 上的应用。通常采用CNN 、LSTM 等深度学习网络自动发现一些模式和特征,然后结合C RF , softmax 等分类算法进行分词预测。
2.6 总结
对比机械分词法,这些统计分词方法不需耗费人力维护词典,能较好地处理歧义和未登录词,是目前分词中非常主流的方法。但其分同的效果很依赖训练语料的质量,且计算量相较于机械分词要大得多。