最短路径问题uva1499详解

这题有两个要求，先是经过的边数最少，在这个前提下要求颜色序列最小。然后输入你的总结点数和总边数，输出你从起点到终点一共会经过几个结点和经过每一条边的颜色序列。首先思考经过的边数最少，这个只能从终点到起点进行bfs，如果是从起点开始扫描左边分支只有2级但是右边有5级终点在右边，这样考虑可能扫描不出来最短路径的长度，所以应该从终点开始进行bfs，然后还要求每一级别最小字典序，这就需要每一级都进行比较选出颜色序列最小，因为是颜色序列所以前面的肯定大于后面的因此只需要考虑在前一级选出最小的，而不是所有路上的颜色值相加，这样就只需要加一条判断使得入队列的都是当前最短路上同时同一级下的颜色序列最小的边连接的下一个结点进行入队列扫描即可。

程序由4个函数组成其中3个小函数1个主函数

前面的头文件主要是STL里面的一些头文件，vector是动态的数组方便存结点或者边数可以大大减少内存的浪费，queue是队列，还有cstring里面的memset函数为了初始化数组，这些后面再说，定义的maxn就是动态数组的行数，每行的空间可以自己分配，g数组里面就是存的连通的结点，与行数代表的这个结点相连接的所有结点都存在这一行里，避免了结点的遗漏，c数组里面存的是图的颜色，每一行存的代表与这一行相连接的所有边的颜色序，n输入的结点数，m要输入的边数，d用来保存每个结点到终点的最小距离，这个ans存放的就是每一级的最小颜色序列，方便最后输出。

1.下面是第一个函数用来录入的

这个函数主要是给g，c两个数组分别录入结点和颜色的，这个录入方式就是可以保证下面的循环可以使得每个结点每个颜色序都可以取到，因为是无向图所以边和相连的结点都要录入两遍，用的函数是vector的内置函数。

2.下面一个函数是用来记录最短路程的

前面说了是从后向前进行遍历找到到起点的最短路径，因此函数将参数设置为总的结点数。

要进行反向的遍历，就要保证每个结点都被遍历到，定义一个队列就可以很好的实现这个功能，先让最后一个结点进 队列。下面就要思考如何判断路到到终点的最短路径，这就需要一个d数组来存放每一级的结点到终点的最短长度，这样看起来思路就比较明确了我们只需要做到2点：一是将每一个结点都不放过全都遍历，同时尽量做到每个结点只遍历一遍。二是按级进行结点到终点长度的记录，同一级的结点到终点的长度都是一样的。

这就进入了这个反向bfs最核心的循环，循环的判断标准是队列为空，当然也可以是循环n-1次作为判断条件都一样。首先将当前队列的首元素取出来，然后根据g数组找到与这个结点相连接的所有结点都要进行下面的for循环，这个for循环主要是为了找到最短的路径长度，因此这个判断条件大体可以分为两个一个是到了起始结点就直接结点数加一而起直接退出循环，如果没到起始的结点也要将结点数加一，但是在这里要考虑一个问题，要保证一个结点只走一次，因为越早的循环走到同一结点所经过的路程越短，所以必须要有一个判断条件使得这个d数组里面放的某一结点到终点的最短距离是最早进入循环的因此在这将整个d数组初始化为-1当然这个操作要在while循环之前进行，用memset函数初始化更简单一些

通过判断下d【next】是不是-1就可以得知next结点在前面的循环中是否出现过，出现过就不进行操作，这样就保证了d里面存放的是这个结点到终点的最短距离，同时这个也可以作为进入队列的条件，使得每个结点进入一次，一次一次的循环最终一定会到d【1】这样就可以求出起点到终点的最短长度并且这个最短长度就存储在d【1】中，到这这个bfs就结束了。

3.正向的bfs进行最小颜色序列的查找

同样的取出队列的首元素然后找出与它相连接的下一级结点都是什么并且循环就不说了，说一下如何找出当前一级最小的颜色序列

这样的寻找同样要保证所有的可能性都包含在内，所以就要将同一级的所有结点进行for循环以便找出最小的颜色序列，首先必须要将不在最短路径上的结点排除，这第一个if判断就起了这个作用。在最短路径上面的想要取出来最小的颜色序列就很简单了只要一个判断就可以了。现在这个mm就存储了某一与下一级相连接的最短路径上最小的颜色序列，这还不够因为同一级的结点还有很多要将这一级所有的结点分别与下一级进行最短路径的选择。

设置这个判断就可以将每一级的结点到下一级的结点的最短距离存放下来，存在ans中，ans中的长度并不是结点到结点的颜色序列而是某一级结点到某一级结点的最小颜色序列。因为这里面存的是某一级结点到下一级结点的最小颜色序列因此下面为了保证没有多余因素的干扰我们只让通过判断的结点进入到队列中进行循环

这个vis数组的判断完全可以不加，加了判断是考虑到重边相同颜色序列并且是相同的两个点相连，为了减小进入队列的点数提高程序运行效率，加了这个判断，第二个判断和第三条件是一定要有的，因为进入队列的点一定得保证在最短路径上，同时也得保证他得和前面的结点可以连起来并保证颜色序列最小，所以同时满足这三个条件进入队列的点不但优化了运行效率还保证了可以得到总的最小的颜色序列

4.主函数就是输入边数调用函数并输出结果了

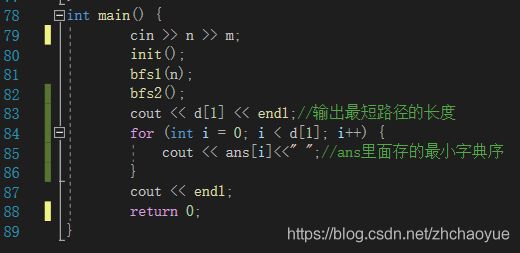
主函数就调用函数就ok了，注意输出的是每一级结点的最小字典序。

#include
#include
#include//memset函数的库
#include
#include
const int maxn = 100005;
using namespace std;
vector g[maxn];//图的连通
vector c[maxn];//图的颜色
int n, m, d[maxn],ans[maxn];//d保存距离，ans保存最小颜色
void init() {
 int x, y, temp;
 for (int i = 0; i < m; i++) {
  cin >> x >> y;
  g[x].push_back(y);//无向图将边录入，里面的每一行就是这个结点相连接的所有结点
  g[y].push_back(x);
  cin >> temp;
  c[x].push_back(temp);//将颜色录入
  c[y].push_back(temp);
 }
}
void bfs1(int n)//进行距离的遍历，完成d数组。
{
 memset(d, -1, sizeof(d));//距离数组全部设置为-1只是为了判断某个结点是不是扫描过
 queueq;//定义一个队列用来一个结点一个结点的扫描，扫一个出队列一个可以防止遗漏新的不停的从后面加进队列中
 q.push(n);//终点先进入队列
 d[n] = 0;
 while (!q.empty()) {//一个一个扫描直到队列为空为止
  int u = q.front(); q.pop();//每次都将队列最前面的一个元素赋值给u用来扫描，然后将这个元素清除
  int sz = g[u].size();//可以测出与某一结点相连接的前方的总结点数，让下面可以一个一个扫描
  for (int v = 0; v < sz; v++) {
   int next = g[u][v];//某个结点相连接的结点取出来
   if (next== 1) {//如果这个结点是初始结点的话这轮扫描就结束，路径总长度加1
    d[1] = d[u] + 1;
    return;
   }
   if (d[next] = -1) {//可能一个结点到下一个结点会有多条路径，这个就保证了只数一次
    d[next] = d[u] + 1;//下一个结点离终点的总路程就会是结点这个结点+1
    q.push(next);//将这个不是初始结点的结点进入队列以便继续向下寻找
   }
  }
 }
}
void bfs2() {//对颜色进行排序，并保存颜色
 queueq;
 q.push(1);//从前往后进行扫描，从1开始向后;
 while (!q.empty()) {//一直扫描到队列为空，终点也出队列为止
  int u = q.front(); q.pop();//取出队列中的第一个元素并且出队列
  if (d[u] ==0)return;//***
  int sz = g[u].size();//正向的和反向的一样为了将与此结点下面的结点都扫描sz的大小为与这个结点相连接的结点数
  int mm = -1;//m随便定义用来记录最小颜色的所以要小于等于0初始的时候
  for (int i = 0;i    int vv = g[u][i];//vv代表的是下一个结点
   if (d[vv] == d[u] - 1) {//到看下一条路的长度是不是到上一条路减去1，这里面d数组里面存放的就是每个位置的时候走的离终点最短的步数
    if (mm == -1)//此处初始化将最小长度下两个结点间最小的字典序记录下来
     mm = c[u][i];
    else
     mm = min(mm, c[u][i]);//最小长度有多条路径，就需要多少次比较
   }
  }
  int t = d[1] - d[u];//t代表的是到下一级的结点，ans里面存的是某一级别的结点的最小距离
  if (ans[t] == 0)ans[t] = mm;
  else
   ans[t] = min(mm, ans[t]);
  int vis[maxn];
  memset(vis,0, sizeof(vis));
  for (int v = 0; v < sz; v++)//将同时满足条件的节点加入队列，并同时进行bfs
  {
   int vv = g[u][v];//vv代表这个结点的下一个结点
   if (vis[vv] == 0 && d[vv] == d[u] - 1 && c[u][v] == mm) {//等于0为了保证同一个结点只录入一次，到下一个结点必须是最小的保证字典序可以连接起来
    q.push(vv);//将下一个结点进入循环
    vis[vv] = 1;//用来记录是否经过这个结点,保证了一个结点进入一次循环而不能重复进入
   }
  }
 }
}
int main() {
     cin >> n >> m;
  init();
  bfs1(n);
  bfs2();
  cout << d[1] << endl;//输出最短路径的长度
  for (int i = 0; i < d[1]; i++) {
   cout << ans[i]<<" ";//ans里面存的最小字典序
  }
  cout << endl;
  return 0;
}

 

上一封 下一封

« 返回再次编辑 撤回回复全部转发删除彻底删除

标记为...

移动到...