深入理解TCP拥塞控制——从BIC到CUBIC
引言
网上的各种博文一提到tcp的拥塞控制,都是清一水的慢启动,拥塞避免,快速重传,呃...虽然没什么问题,但是这都9012年了,tcp的拥塞控制算法已经演变了很多了,在linux内核2.6.8中,就默认采用BIC拥塞控制算法了,在2.6.18中,默认的拥塞控制算法采用了CUBIC,网上各种讲CUBIC的不算太多,个人觉得这篇博文讲的还不错,但该文偏向于从宏观和趋势的角度去理解CUBIC,对于某些细节就少了一些说明,而且虽然那篇博文虽说是简化了公式推导,但我感觉他把公式理解的太复杂化了,因此,才有了本文,本文的目的在于帮大家更细节化的了解BIC和CUBIC的由来及细节,同时简化大家对CUBIC的公式理解。OK,下面开始我们的正文。
BIC诞生的缘由
任何事物的产生与兴起一定有他的缘由,为什么诞生了BIC,又诞生了CUBIC?一定是tcp_reno有他不好用的地方,我们来回忆一下reno的拥塞控制流程,也就是大家熟悉的慢启动,拥塞避免,快速重传,盗用一张经典的图:
![]()
我们知道,在reno版本的拥塞控制下,进入拥塞避免状态或快速恢复状态后,每经过一个RTT才会将窗口大小加1,那么问题来了,假设我们链路状况好,但如果RTT很长的话,reno不就要很长时间才能达到最佳拥塞窗口了吗?知道了这一点,你也就知道了为什么会产生tcp_BIC,BIC(Binary Increase Congestion control) 的中文名我也不清楚该怎么叫,但我建议大家理解成二分搜索拥塞控制算法,为什么这么说呢?因为BIC的核心思想就是通过二分搜索的思想来找到当前链路最合适的拥塞窗口,下面我们来详细阐述下BIC算法的主要流程。
BIC算法流程
显然,当前链路在网络上因为排队而发生丢包时,链路的当前最佳拥塞窗口肯定是小于丢包时的拥塞窗口的,我们称丢包时的拥塞窗口大小为Wmax,同样,BIC也采用乘法减小的方式减小窗口,我们称这个因子为![]() ,同时,我们称减小后的窗口为Wmin,则有Wmin=
,同时,我们称减小后的窗口为Wmin,则有Wmin=![]() *Wmax,我们认为乘法减小后的窗口应该是小于最佳拥塞窗口的,因此,对于链路当前最佳拥塞窗口W来说,我们有Wmin<W<Wmax,reno采用加法去搜索W的方式实在是太慢了,因此BIC采用了二分搜索的方式去找到这个W,二分搜索的具体流程就不赘述了,我们来看看这么做的好处,首先我们来看下BIC的拥塞窗口图像:
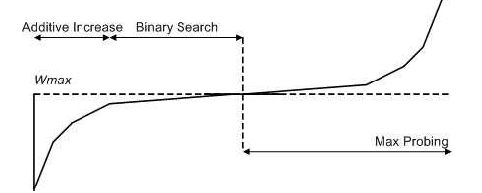
*Wmax,我们认为乘法减小后的窗口应该是小于最佳拥塞窗口的,因此,对于链路当前最佳拥塞窗口W来说,我们有Wmin<W<Wmax,reno采用加法去搜索W的方式实在是太慢了,因此BIC采用了二分搜索的方式去找到这个W,二分搜索的具体流程就不赘述了,我们来看看这么做的好处,首先我们来看下BIC的拥塞窗口图像:
我们看虚线左边的图像,也就是加法增窗(Additive Increase),二分搜索(Binary Search)的过程,整个增窗流程趋近一个凸函数的左半边,这样带来的好处是:越接近Wmax附近,窗口的增加速度越慢,这也就意味着,在一次经历了一次丢包后,窗口会更快的接近W,并在W附近停留更多的时间(对比reno的锯齿形图像可以有更明显的感觉)。当然你可能会觉得,W如果在Wmin附近呢?不是更快超过了吗?如果你产生了这样的疑问,你需要明确一个观点,对于整个网络来说,我们需要的是最终的收敛,而不是一次的收敛,网络拥塞丢包的大部分情况是,当前网络中所有的连接占满了带宽,此时有一个新链路加进来,那么新链路争抢资源过程则势必会引起丢包,合适的做法应当是,现有的各条链路让出部分资源,让新的链路可以和旧链路一样公平的拿到其应得的资源。所以,我们需要的是最终收敛,所有链路快速且公平的拿到带宽资源,因此,我们衡量一个拥塞控制算法的优劣时,会看他的收敛速度,公平性。回到刚才的问题上来,W如果在Wmin附近也并不影响,BIC会快速进入到下一次增窗过程中去,然后达到最终收敛。
再来看虚线右边的图像,这个过程被称作最大窗探测过程(Max Probing),顾名思义,这个过程就是在探测当前合适的最大窗口,为什么要设计成这样呢?BIC算法的设计者认为,当窗口Wmax超过以后,如果还未发生丢包,则说明网络变好了,或者有部分链接让出了资源,那么我们要尽可能的去抢占他,首先我们先慢慢的尝试,然后越来越快,以保证整个网络资源的利用率,因此Max Probing被设计为虚线左边的旋转对称的模样。当然,Max Probing的增窗过程真的合理吗?它确实保证了快速收敛,但对于其公平性(相对于tcp_reno,网络上会同时存在大量拥塞算法),可能要打一个问号。
关于BIC,这里再说一些细节上的东西,出于工程实现和现实应用的考虑,在窗口调整过程中设置了一个Smax及Smin的阈值,当窗口的增量大于时,增量则设为,当窗口增量为时,则将当前窗口设为Wmax,也就是说窗口已经通过二分搜索达到了最大值,可以开始Max Probing阶段了,具体原因很好理解,不赘述了。
CUBIC诞生的缘由
从感觉上来说,BIC在long fast的网络场景下表现的已经很好了,为什么又产生了CUBIC呢?首先,如果你设计了一个新东西,你肯定希望能把他应用的更广泛,那么BIC能不能用到RTT较小,丢包较高的环境中呢?我们知道tcp_reno已经广泛的应用在了网络中,同时还有HSTCP,tcp_WestWood,tcp_vegas等,一个新协议的出现不可能马上替换掉所有旧的,而根据我们前面的分析,BIC在离Wmax较远时,窗口增速很快,如果将BIC广泛应用到RTT较小,丢包较高的网络中去,BIC的增窗策略太激进了,大量的抢占了资源,公平性实在是难以保证。同时,BIC的二分搜索增窗,Max Probing的指数增窗,Smax及Smin的限定,实现相对复杂(呃...好吧,相对CUBIC确实复杂很多),同时也很难以对性能进行分析,于是,诞生了我们的CUBIC。CUBIC的名字很有意思,cubic本来就是立方的意思,而又可以理解成cu-bic,也就是cubic-BIC的样式,感觉上就有点GNU取名的味道。从名字上我们知道CUBIC是跟立方有关的,下面我们来详细介绍CUBIC的整体流程。
CUBIC算法流程
知道了BIC的存在的问题,也就知道了CUBIC的核心思想,CUBIC解决问题的思路很巧妙,既要BIC的高效,又要公平性,要实现BIC的高效只需要窗口调整过程的图像类似BIC即可,任意一个奇数阶的多项式图像均可以拟合BIC的图像,对于公平性而言,既然reno和BIC都以RTT为单位争抢资源,那么为什么不能把窗口的调整过程从以RTT为单位的思路独立出来呢?这样就可以通过调整时间的步长来维持公平性。CUBIC通过这个公式给出了解决方案:
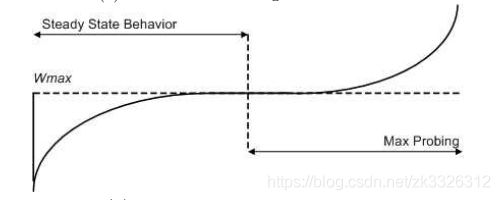
关于K的推导是一个很简单的方式,我们先来看这个函数的图像:
CUBIC和BIC是类似的,同样也是乘法减小的过程,那么也就意味着t=0时刻,窗口是我们的Wmin,也就是![]() *Wmax,把t=0,W(0)=
*Wmax,把t=0,W(0)=![]() *Wmax带入,解出来
*Wmax带入,解出来
这也就为什么我在开篇说的那篇博文中对于K的解释太繁琐了,讲到这里,其实CUBIC的核心也差不多讲完了,CUBIC将BIC的二分搜索过程和Max Probing以公式的形式独立出来,剥离了其对RTT的依赖,同时这也大量减轻了代码负担,一个公式就全部搞定了。再说一点CUBIC的细节吧,CUBIC可以通过调整C和![]() 来调整窗口调整速度,来保证公平性和性能的协调(关于C和
来调整窗口调整速度,来保证公平性和性能的协调(关于C和![]() 这一块的取值证明大家可以自己搜论文看看,不得不说很多东西有公式量化就很方便分析了)。然而在实际应用中,CUBIC发现在有些时刻还是有点抢不过reno,因此CUBIC还增加了一些细节策略,比如:在一次丢包事件后,经过t时间,如果CUBIC的增窗速度小于标准TCP,则,采用标准TCP增加的窗口大小。
这一块的取值证明大家可以自己搜论文看看,不得不说很多东西有公式量化就很方便分析了)。然而在实际应用中,CUBIC发现在有些时刻还是有点抢不过reno,因此CUBIC还增加了一些细节策略,比如:在一次丢包事件后,经过t时间,如果CUBIC的增窗速度小于标准TCP,则,采用标准TCP增加的窗口大小。
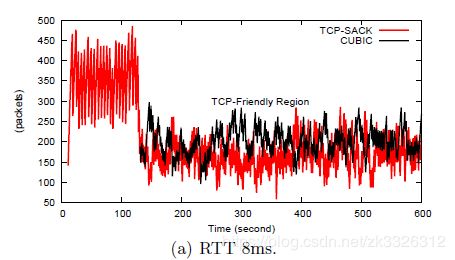
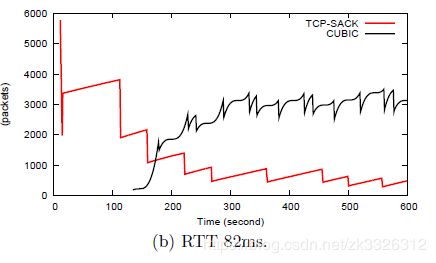
好吧,文章的最后我们来看看CUBIC的公平性以及在long fast网络中的性能优势:
本文的数据以及某些思路来源于这篇论文:CUBIC: A New TCPFriendly HighSpeed TCP Variant
有兴趣的朋友可以自行下载。