SAC（Soft Actor-Critic）

Hi，这是第三篇算法简介呀

论文链接：Soft Actor-Critic:Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor，2018，ICML

文章概述

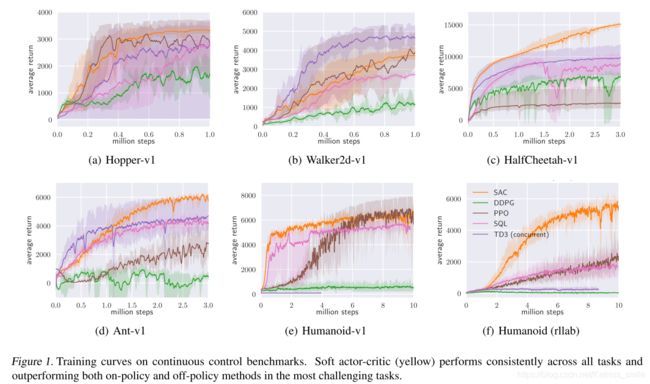
  强化学习的两个主要挑战是高样本复杂性和收敛性脆弱。在这篇文章中，提出了一个基于最大熵框架的actor-critic离线策略的深度强化学习算法SAC（Soft Actor-Critic）。在DDPG中，policy和Q-value之间相互作用，使得其不稳定，容易受超参数影响。在SQL中，将actor网络作为近似采样器，而不是actor-critic算法中真正的actor，收敛取决于采样值和真实后验值的近似程度。
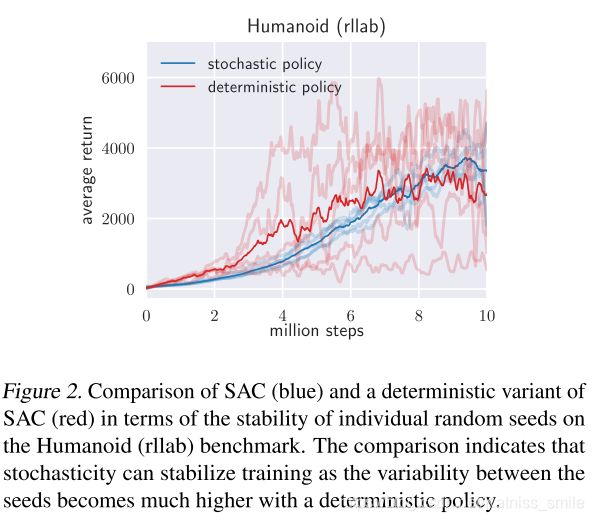
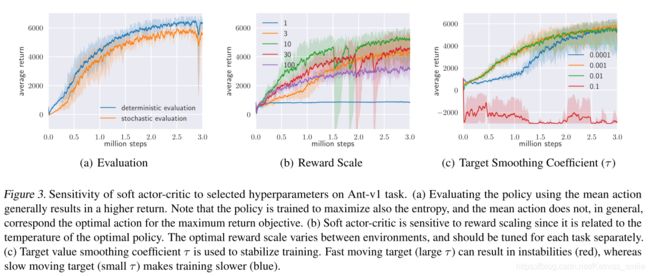
  最大熵强化学习是将最大熵项加在reward上，其目的是鼓励探索环境，希望学到的策略在优化目标的同时尽可能地随机，同时保持在各个有希望的方向上的可能性，而不是很快收敛到一个局部最优。使用温度参数$\alpha$来决定熵对reward的影响，当$\alpha$趋近于0时，则reward退化为传统强化学习reward。
  第一个在最大熵框架下，使用off-policy更新策略的算法。
  总共包含四个网络：策略网络（$\varphi$），value网络和对应的目标网络（$\psi$和$\overline{\psi }$），Q-value网络（$\theta$）。

公式理解

$$J(\pi )=\sum _{t=0}^T{\mathbb{E}}_{\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\sim {\rho }_{\pi }}\left[r\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)+\alpha \mathcal{H}\left(\pi \left(\cdot |{\mathbf{s}}_t\right)\right)\right]$$

$$\begin{array}{l}{\mathcal{T}}^{\pi }Q\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\triangleq r\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)+\gamma {\mathbb{E}}_{{\mathbf{s}}_{t+1}\sim p}\left[V\left({\mathbf{s}}_{t+1}\right)\right]\\ \text{ where }\\ V\left({\mathbf{s}}_t\right)={\mathbb{E}}_{{\mathbf{a}}_t\sim \pi }\left[Q\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)-\log \pi \left({\mathbf{a}}_t|{\mathbf{s}}_t\right)\right]\end{array}$$

$${\pi }_{\text{new }}=\arg \underset{{\pi }^{\prime }\in \Pi }{\min }{\mathrm{D}}_{\mathrm{K}\mathrm{L}}\left({\pi }^{\prime }\left(\cdot |{\mathbf{s}}_t\right)||\frac{\exp \left(Q^{{\pi }_{\text{old }}}\left({\mathbf{s}}_t,\cdot \right)\right)}{Z^{{\pi }_{\text{old }}}\left({\mathbf{s}}_t\right)}\right)$$

$$J_V(\psi )={\mathbb{E}}_{{\mathbf{s}}_t\sim \mathcal{D}}\left[\frac{1}{2}{\left(V_{\psi }\left({\mathbf{s}}_t\right)-{\mathbb{E}}_{{\mathbf{a}}_t\sim {\pi }_{\varphi }}\left[Q_{\theta }\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)-\log {\pi }_{\varphi }\left({\mathbf{a}}_t|{\mathbf{s}}_t\right)\right]\right)}^2\right]$$

$${\hat{\nabla }}_{\psi }{J}_V(\psi )={\nabla }_{\psi }{V}_{\psi }\left({\mathbf{s}}_t\right)\left(V_{\psi }\left({\mathbf{s}}_t\right)-Q_{\theta }\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)+\log {\pi }_{\varphi }\left({\mathbf{a}}_t|{\mathbf{s}}_t\right)\right)$$

$$J_Q(\theta )={\mathbb{E}}_{\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\sim \mathcal{D}}\left[\frac{1}{2}{\left(Q_{\theta }\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)-\hat{Q}\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right)}^2\right]$$  其中，$\hat{Q}\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)=r\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)+\gamma {\mathbb{E}}_{{\mathbf{s}}_{t+1}\sim p}\left[V_{\overline{\psi }}\left({\mathbf{s}}_{t+1}\right)\right]$

$$J_{\pi }(\varphi )={\mathbb{E}}_{{\mathbf{s}}_t\sim \mathcal{D}}\left[{\mathrm{D}}_{\mathrm{K}\mathrm{L}}\left({\pi }_{\varphi }\left(\cdot |{\mathbf{s}}_t\right)\Vert \frac{\exp \left(Q_{\theta }\left({\mathbf{s}}_t,\cdot \right)\right)}{Z_{\theta }\left({\mathbf{s}}_t\right)}\right)\right]$$

$$J_{\pi }(\varphi )={\mathbb{E}}_{{\mathbf{s}}_t\sim \mathcal{D},{ϵ}_t\sim \mathcal{N}}\left[\log {\pi }_{\varphi }\left(f_{\varphi }\left({ϵ}_t;{\mathbf{s}}_t\right)|{\mathbf{s}}_t\right)-Q_{\theta }\left({\mathbf{s}}_t,f_{\varphi }\left({ϵ}_t;{\mathbf{s}}_t\right)\right)\right]$$

$$\begin{array}{l}{\hat{\nabla }}_{\varphi }{J}_{\pi }(\varphi )={\nabla }_{\varphi }\log {\pi }_{\varphi }\left({\mathbf{a}}_t|{\mathbf{s}}_t\right)+\left({\nabla }_{{\mathbf{a}}_t}\log {\pi }_{\varphi }\left({\mathbf{a}}_t|{\mathbf{s}}_t\right)-{\nabla }_{{\mathbf{a}}_t}Q\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right){\nabla }_{\varphi }{f}_{\varphi }({ϵ}_t;{\mathbf{s}}_t)\end{array}$$

伪代码分析

实验结果分析

• 不同方法在不同场景下的平均reward
  
• 随机策略与确定性策略的稳定性对比
  
• 对所选超参数的敏感性