CS231n Spring 2019 Assignment 3—Generative Adversarial Networks (GANs)对抗生成网络

---

终于来到了cs231n的最后一次作业，在Generative_Adversarial_Networks_PyTorch.ipynb内完成编程练习就好了。这次的对抗生成网络(GANs)个人感觉比之前的两节有关可视化和伪图片的生成要更难一点，当然思路也是更加新颖不一样了，下面就根据教程里面大致介绍一下"干(GAN)"！

What is a GAN?

我们之前接触的神经网络模型都是输入一张图片给出分类标签的判别模型(discriminative models)，现在拓展一下，学习一下能够生成训练数据分布的图像的生成模型(generative models)，而对抗生成网络(GANs)就是包含这两方面模型的方法。

GAN是Goodfellow等人在2014年提出的一种训练生成模型的方法，在其中我们会构建两种不同的神经网络：

• 判别器(discriminator)：传统的分类网络，训练它是为了尽可能正确判别输入的图片是否来自于训练集（是就认为real，不是就认为fake）；
• 生成器(generator)：一种将随机噪声作为输入，经过神经网络的变换进而产生图像的网络，它的目标就是愚弄判别器，让它把生成器生成的图像判别为real。

下面的这张示意图可以给我们一个初始的概念：

在网上其他的地方看到一个形象的比喻，感觉写得比较好，摘抄如下：

比如，有一个业余画家总喜欢仿造著名画家的画，把仿造的画和真实的画混在一起，然后有一个专家想办法来区分那些是真迹，那些是赝品。通过不断的相互博弈，业余画家的仿造能力日益上升，与此同时，通过不断的判断结果反馈，积累了不少经验，专家的鉴别能力也在上升，进一步促使业余专家的仿造能力大幅提升，最后使得业余专家的仿造作品无限接近与真迹，使得鉴别专家无法辨别，最后判断的准确率为0.5。

用数学语言描述一下这个博弈(game-theoretic)的过程：
$$\underset{G}{\mathrm{minimize}}\underset{D}{\mathrm{maximize}}{\mathbb{E}}_{x\sim p_{\text{data}}}\left[\log D(x)\right]+{\mathbb{E}}_{z\sim p(z)}\left[\log \left(1-D(G(z))\right)\right]$$其中$z\sim p(z)$代表随机噪声样本，$x\sim p_{\text{data}}$代表的是训练数据，$G(z)$代表用生成器$G$生成的图像，$D$就代表判别器的输出，可以认为是输入图像是real的概率，那相应的$D(x)$就是把训练图像判别为real的概率，而$D(G(z))$就是把生成器生成的图像判别为real的概率。$\mathbb{E}$是期望的意思。Goodfellow et al.分析了这个博弈过程是如何与减小训练数据与生成样本分布的Jensen-Shannon divergence有关的。

为了优化这个极大极小博弈(minimax game)过程，我们需要交替(aternate)地对$G$的目标进行梯度下降，对$D$的目标进行梯度上升：

1. 更新生成器$G$去最小化判别器正确判别的概率（似乎in practice不太好用，而采用：更新生成器$G$去最大化判别器犯错误的概率），即$D(G(z))$接近１：$$\underset{G}{\mathrm{maximize}}{\mathbb{E}}_{z\sim p(z)}\left[\log D(G(z))\right]\text{\hspace{1em}(1)}$$
2. 更新判别器$D$去最大化判别器正确判别的概率，即$D(x)$接近１，$D(G(z))$接近0：$$\underset{D}{\mathrm{maximize}}{\mathbb{E}}_{x\sim p_{\text{data}}}\left[\log D(x)\right]+{\mathbb{E}}_{z\sim p(z)}\left[\log \left(1-D(G(z))\right)\right]\text{\hspace{1em}(2)}$$

当然为了更加可靠地训练GAN，有很多的方法被提出来，包括该损失函数和生成器模型的，下面的“LS-GAN”部分和“DC-GAN”部分就是，更多可以学习GANs的教程和深度学习花书中深层生成模型章节。有了上面的认知以后，下面的代码编写就会轻松明朗一些，这是教程开头给出的可能会生成的图：

下面就正式进入编程部分！

Vanilla GAN

这部分就是用上面论文说到的方法，不怎么更改，所以称为vanilla GAN。

Random Noise

第一个要编写的代码就是产生-1到1之间均匀分布的噪声，可是torch.rand返回的是[0,1)之间的均匀分布，用个小手段就行：

def sample_noise(batch_size, dim):
    """
    Generate a PyTorch Tensor of uniform random noise.

    Input:
    - batch_size: Integer giving the batch size of noise to generate.
    - dim: Integer giving the dimension of noise to generate.
    
    Output:
    - A PyTorch Tensor of shape (batch_size, dim) containing uniform
      random noise in the range (-1, 1).
    """
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    noise = 2 * torch.rand(batch_size, dim) - 1
    return noise

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

Discriminator

到这里就要来搭建一个判别器模型了，这里是都是全连接加上LeakyReLU，根据jupyter notebook中给出的架构，调用torch.nn就像搭积木一样搭建网络模型，不过要注意的一点就是针对MNIST数据集，判别器的输入shape是(batch_size,1,28,28)，这是我看train部分后分析出来的，所以要有个Flatten()操作，经过discriminator后shape变为(batch_size,1)：

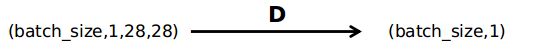
def discriminator():
    """
    Build and return a PyTorch model implementing the architecture above.
    """
    model = nn.Sequential(
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        
        Flatten(), # [batch_size, dim] # don't forget comma
        # Why use Flatten()? 
        # Because in loader_train, tensor shape is (batch_size,1,28,28) [see train part]
        # inplace为True，将会改变输入的数据 ，否则不会改变原输入，只会产生新的输出，节省显存
        # nn.LeakyReLU(alpha, inplace=True)
        # torch.nn.Linear(in_features, out_features, bias=True)
        nn.Linear(784, 256),
        nn.LeakyReLU(0.01),
        nn.Linear(256, 256),
        nn.LeakyReLU(0.01),
        nn.Linear(256, 1)

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    )
    return model

Generator

接下来就是生成器的结构编写，也是看着提示编写就行，与判别器不一样的是，生成器的输入shape是(batch_size, noise_dim)，所以就不需要Flatten()操作，反而在最后加个nn.Tanh()函数将输出限制在 [-1,1]内，经过generator后shape变为(batch_size, 784)：

def generator(noise_dim=NOISE_DIM):
    """
    Build and return a PyTorch model implementing the architecture above.
    """
    model = nn.Sequential(
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        
        # Flatten(),
        # Why here not use Flatten()? 
        # Because generator model input shape is (batch_size, noise_dim) [see train part]
        nn.Linear(noise_dim, 1024),
        nn.ReLU(),
        nn.Linear(1024, 1024),
        nn.ReLU(),
        nn.Linear(1024, 784),
        nn.Tanh()

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    )
    return model

GAN Loss

根据上面的$(1)(2)$可以得到GAN的损失，分为两部分，一部分就是generator loss：
$${\ell }_G=-{\mathbb{E}}_{z\sim p(z)}\left[\log D(G(z))\right]\text{\hspace{1em}(3)}$$另一部分是discriminator loss：$${\ell }_D=-{\mathbb{E}}_{x\sim p_{\text{data}}}\left[\log D(x)\right]-{\mathbb{E}}_{z\sim p(z)}\left[\log \left(1-D(G(z))\right)\right]\text{\hspace{1em}(4)}$$这里与$(1)(2)$相比多了个负号，主要这里定义的是损失，所以要减小loss。可以看到，针对生成器，就是要最大化判别器将之生成的图像判别为real的概率，也就是$D(G(z))$，当$D(G(z))$越大时(当然不能大过1)，则生成器损失${\ell }_G$越小。针对判别器，要最大化将训练图像判别为real的概率，也就是要增大$D(x)$；也要尽可能地最小化将生成器生成的图片判断为real的概率，也就是减小$D(G(z)$，这样判别器损失${\ell }_D$就越小。

看到这里会感觉损失函数与二分类交叉熵损失函数(binary cross entropy loss)形式比较接近，考虑可用那个损失函数，最后再加个平均操作就行。给定一个分值 $s\in \mathbb{R}$ 和真实标签 $y\in \{0,1\}$，则二分类交叉熵损失为：
$$bce(s,y)=-y\ast \log (s)-(1-y)\ast \log (1-s)\text{\hspace{1em}(5)}$$一般的分值$s$都是经过sigmoid或者softmax后的概率，经过这些压缩函数之前都是未进行归一化和e指数操作的logits，经过e指数操作后会产生数值不稳定的情况（最主要的还是怕$e^{num}$当num为一个很大的正值时会发生溢出），所以给出了数值稳定的二分类交叉熵损失函数（当然这部分教程里面已经给出，这里只是分析一下），从给出的网址可以看到推导过程：tf.nn.sigmoid_cross_entropy_with_logits从名字就可以看出来，score是由logits经过sigmoid函数而来，假设$x=logits,z=labels$，则损失为(这里$log$就是$ln$)：
$$\begin{array}{rl}bc{e}_{loss}& =z\ast -log(\sigma (x))+(1-z)\ast -log(1-\sigma (x))\\ & =z\ast -log(\frac{1}{1+e^{-x}})+(1-z)\ast -log(\frac{e^{-x}}{1+e^{-x}})\\ & =z\ast log(1+e^{-x})+(1-z)\ast (-log(e^{-x})+log(1+e^{-x}))\\ & =z\ast log(1+e^{-x})+(1-z)\ast (x+log(1+e^{-x}))\\ & =(1-z)\ast x+log(1+e^{-x})\\ & =x-x\ast z+log(1+e^{-x})\\ & =log(e^x)-x\ast z+log(1+e^{-x})\\ & =-x\ast z+log(1+e^x)\end{array}$$最后将上面红色和蓝色合并写成一个公式就是(仔细看下面的公式，当$x$为正时，就是上面的红色公式；当$x$为负时，就是上面的蓝色公式，总之就是使e的指数为负值)：
$$bc{e}_{loss}=-x\ast z+max(x,0)+log(1+e^{-abs(x)})$$所以这就有了教程里面的bce_loss()函数，对于discriminator_loss和generator_loss，只要知道logits_fake就是$D(G(z))$，logits_real就是$D(x)$就能够编出来了，这里确实需要理解一下：

def discriminator_loss(logits_real, logits_fake):
    """
    Computes the discriminator loss described above.
    
    Inputs:
    - logits_real: PyTorch Tensor of shape (N,) giving scores for the real data.
    - logits_fake: PyTorch Tensor of shape (N,) giving scores for the fake data.
    
    Returns:
    - loss: PyTorch Tensor containing (scalar) the loss for the discriminator.
    """
    loss = None
    # My code start
    real_labels = torch.ones_like(logits_real).type(dtype)
    fake_labels = 1 - real_labels
    loss_from_data = bce_loss(logits_real, real_labels)
    # this "logits_fake" is equivalent to "logits_fake" from generator_loss()
    loss_from_sample = bce_loss(logits_fake, fake_labels) 
    loss = loss_from_data + loss_from_sample
    
    # My code end
    
    return loss

def generator_loss(logits_fake):
    """
    Computes the generator loss described above.

    Inputs:
    - logits_fake: PyTorch Tensor of shape (N,) giving scores for the fake data.
    
    Returns:
    - loss: PyTorch Tensor containing the (scalar) loss for the generator.
    """
    loss = None
    # My code start
    fake_labels = torch.ones_like(logits_fake).type(dtype)
    loss = bce_loss(logits_fake, fake_labels)
    # My code end
    
    return loss

Optimizing our loss

优化部分很简单，就一句话，主要要知道PyTorch里面optim类的函数输入参数就行：

def get_optimizer(model):
    """
    Construct and return an Adam optimizer for the model with learning rate 1e-3,
    beta1=0.5, and beta2=0.999.
    
    Input:
    - model: A PyTorch model that we want to optimize.
    
    Returns:
    - An Adam optimizer for the model with the desired hyperparameters.
    """
    optimizer = None
    # My code start
    # torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)
    optimizer = optim.Adam(model.parameters(), lr = 1e-3, betas=(0.5, 0.999))
    # My code end
    return optimizer

LS-GAN

只要完成了上面的训练，下面就是改动一下损失函数就行了，LS-GAN是Least Squares GAN的简称，它就是把生成器和判别器的损失函数都改了一下，说是更加稳定，生成器损失(generator loss)：$${\ell }_G=\frac{1}{2}{\mathbb{E}}_{z\sim p(z)}\left[{\left(D(G(z))-1\right)}^2\right]$$判别器损失(discriminator loss)：$${\ell }_D=\frac{1}{2}{\mathbb{E}}_{x\sim p_{\text{data}}}\left[{\left(D(x)-1\right)}^2\right]+\frac{1}{2}{\mathbb{E}}_{z\sim p(z)}\left[{\left(D(G(z))\right)}^2\right]$$接着得知道scores_real就是之前的logits_real，也就是$D(x)$；scores_fake就是之前的logits_fake，也就是$D(G(z))$，就可以编得出来了：

def ls_discriminator_loss(scores_real, scores_fake):
    """
    Compute the Least-Squares GAN loss for the discriminator.
    
    Inputs:
    - scores_real: PyTorch Tensor of shape (N,) giving scores for the real data.
    - scores_fake: PyTorch Tensor of shape (N,) giving scores for the fake data.
    
    Outputs:
    - loss: A PyTorch Tensor containing the loss.
    """
    loss = None
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    
    loss_real = 0.5 * (scores_real - torch.ones_like(scores_real).type(dtype))**2 + 0.5 * scores_fake**2
    loss = loss_real.mean()

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    return loss

def ls_generator_loss(scores_fake):
    """
    Computes the Least-Squares GAN loss for the generator.
    
    Inputs:
    - scores_fake: PyTorch Tensor of shape (N,) giving scores for the fake data.
    
    Outputs:
    - loss: A PyTorch Tensor containing the loss.
    """
    loss = None
    # My code start
    loss = 0.5 * (scores_fake - torch.ones_like(scores_fake).type(dtype))**2
    loss = loss.mean()
    # My code end
    
    return loss

DC-GAN

DC-GAN是Deeply Convolutional GANs的简称，原初来自于Ian Goodfellow的GAN里面网络结构都是线性层，没有卷积，而我们应用DCGAN的想法，就是构造模型时使用卷积神经网络和BatchNorm操作，会使得生成的图像更逼真。

DC-Discriminator

对于判别器来说，这里没有什么问题，就是常规的卷积操作，对于一些超参数，别人也给你指定好了，如果想了解更多，可以看官网torch.nn.Conv2d的一些输入输出形状之间的关系，里面还有很多不常用的超参数，也可以参考我的代码注释：

def build_dc_classifier():
    """
    Build and return a PyTorch model for the DCGAN discriminator implementing
    the architecture above.
    """
    return nn.Sequential(
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        
        # MNIST is gray image with 28 * 28 pixels
        # nn.Conv2d(self, in_channels, out_channels, 
        # kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True))
        Unflatten(batch_size, 1, 28, 28), # actually, this layer is not necesssary
        nn.Conv2d(1, 32, kernel_size=5, stride=1), # (batch_size, 32, 24, 24)
        nn.LeakyReLU(0.01),
        nn.MaxPool2d(2, stride=2), # (batch_size, 32, 12, 12)
        nn.Conv2d(32, 64, kernel_size=5, stride=1), # (batch_size, 64, 8, 8)
        nn.LeakyReLU(0.01),
        nn.MaxPool2d(2, stride=2), # (batch_size, 64, 4, 4)
        Flatten(), # (batch_size, 64*4*4)
        nn.Linear(4*4*64, 4*4*64),
        nn.LeakyReLU(0.01),
        nn.Linear(4*4*64, 1) # (batch_size, 1)

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    )

data = next(enumerate(loader_train))[-1][0].type(dtype) # torch.Size([128, 1, 28, 28])
b = build_dc_classifier().type(dtype)
out = b(data)
print(out.size())

DC-Generator

对于生成器来说，会有一点小小的问题，一开始就是找不出来，还是一步一步把shape写出来，才发现之前的tensor是2维的，只能用torch.nn.BatchNorm1d()函数，而后来经过Unflatten()操作展开成4维以后，就可以用torch.nn.BatchNorm2d()函数，而之前没用过的转置卷积torch.nn.ConvTranspose2d()，参数指定后编写也不难，都是模块化操作，具体可见官网文档：

def build_dc_generator(noise_dim=NOISE_DIM):
    """
    Build and return a PyTorch model implementing the DCGAN generator using
    the architecture described above.
    """
    return nn.Sequential(
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        # nn.BatchNorm1/2d(num_features,eps=1e-05,momentum=0.1,affine=True,track_running_stats=True)
        # nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0,...)
        nn.Linear(noise_dim, 1024), # [batch_szie, 1024]
        nn.ReLU(),
        nn.BatchNorm1d(1024),  # Note:not BatchNorm2d # [batch_szie, 1024]
        nn.Linear(1024, 7*7*128),# [batch_szie, 7*7*128]
        nn.ReLU(),
        nn.BatchNorm1d(7*7*128), # Note:not BatchNorm2d # [batch_szie, 7*7*128]
        Unflatten(batch_size, 128, 7, 7),
        nn.ConvTranspose2d(128, 64, kernel_size=4, stride=2, padding=1),
        nn.ReLU(), # (batch_size, 64, 14, 14)
        nn.BatchNorm2d(64),  # (batch_size, 64, 14, 14)
        nn.ConvTranspose2d(64, 1, kernel_size=4, stride=2, padding=1),
        nn.Tanh(), # (batch_size, 1, 28, 28)
        Flatten(), # (batch_size, 784)
        

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    )

test_g_gan = build_dc_generator().type(dtype)
test_g_gan.apply(initialize_weights)

fake_seed = torch.randn(batch_size, NOISE_DIM).type(dtype) # torch.Size([128, 96])
fake_images = test_g_gan.forward(fake_seed)
fake_images.size()

结果

训练代码都已经给出，阅读理解完对自己整体理解会很有帮助。下面就是我三种不同方法得到的生成器生成的图：
通过Vanilla GAN得到的生成图像：
通过Least Squares GAN得到的生成图像：
通过Deeply Convolutional GAN得到的生成图像，可以看到生成质量明显好于前两种方法：
这里也放一下我最后的思考题的answer吧，我不太确定，欢迎有理解的可以下发留言交流：

$y_0$	$y_1$	$y_2$	$y_3$	$y_4$	$y_5$	$y_6$
1	2	1	-1	-2	-1	1
$x_0$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$
1	-1	-2	-1	1	2	1

链接

前面的作业博文请见：

• 上一次的博文：StyleTransfer-PyTorch风格迁移