代码复杂度问题,coverity代码静态分析工具检查
在我们平时写代码的时候总是会不经意的写出复杂度很高的代码:
下面是coverity官方的文字翻译:可以跳过阅读
Basic criteria and methodology
A Cognitive Complexity score is assessed according to three basic rules:
- Ignore structures that allow multiple statements to be readably shorthanded into one
- Increment (add one) for each break in the linear flow of the code
- Increment when flow-breaking structures are nested
Additionally, a complexity score is made up of four different types of increments:
A. Nesting - assessed for nesting control flow structures inside each other
B. Structural - assessed on control flow structures that are subject to a nesting increment, and that increase the nesting count
C. Fundamental - assessed on statements not subject to a nesting increment
D. Hybrid - assessed on control flow structures that are not subject to a nesting increment, but which do increase the nesting count
基本标准和方法
认知复杂性分数根据三个基本规则进行评估: - 忽略允许多个语句可读短手为一个的构造
- 代码线性流中每个中断的增量(添加一个)
- 嵌套分流结构时的增量
此外,复杂性分数由四种不同类型的增量组成:
A. 嵌套 - 评估彼此内部的嵌套控制流结构
B. 结构 - 对受嵌套约束的控制流结构进行评估增量,并增加嵌套计数
C. 基本 - 对不受嵌套增量约束的语句进行评估
D. 混合 - 对不受嵌套约束的控制流结构进行评估增量,但增加嵌套计数
While the type of an increment makes no difference in the math - each increment adds one to the final score - making a distinction among the categories of features being counted
makes it easier to understand where nesting increments do and do not apply.
These rules and the principles behind them are further detailed in the following sections.
虽然增量的类型在数学上没有区别 - 每个增量都会增加一个到最终的分数 - 区分被计数的功能类别便于理解嵌套增量在何处应用和不适用。
这些规则及其背后的原则将在以下各节中进一步详细介绍。
Ignore shorthand
A guiding principle in the formulation of Cognitive Complexity has been that it should incent good coding practices.
That is, it should either ignore or discount features that make code more readable.
The method structure itself is a prime example.
Breaking code into methods allows you to condense multiple statements into a single, evocatively named call, i.e. to “shorthand” it.
Thus, Cognitive Complexity does not increment for methods.
Cognitive Complexity also ignores the null-coalescing operators found in many languages,
again because they allow short-handing multiple lines of code into one. For example, both of the following code samples do the same thing:
忽略速记
认知复杂性的表述的指导原则是,它应该激励良好的编码实践。
也就是说,它应该忽略或折扣使代码更具可读性的功能。
方法结构本身就是一个典型的例子。
将代码分解为方法允许您将多个语句压缩为一个令人回味的命名调用,即"速记"它。
因此,对于方法来说,认知复杂性不会增加。
认知复杂性也忽略了在许多语言中发现的空合并运算符,
再次,因为他们允许短处理多行代码成一个。例如,以下两个代码示例执行相同的操作:
MyObj myObj = null; MyObj myObj = a?.myObj;
if (a != null) {
myObj = a.myObj;
}
The meaning of the version on the left takes a moment to process, while the version on the
right is immediately clear once you understand the null-coalescing syntax. For that reason,
Cognitive Complexity ignores null-coalescing operators.
左侧版本的含义需要片刻来处理,而版本在一旦您理解了空合并语法,right 就会立即清除。因此,认知复杂性忽略空合并运算符。
Increment for breaks in the linear flow
Another guiding principle in the formulation of Cognitive Complexity is that structures that
break code’s normal linear flow from top to bottom, left to right require maintainers to work
harder to understand that code. In acknowledgement of this extra effort, Cognitive
Complexity assesses structural increments for:
线性流中中断的增量
认知复杂性表述的另一个指导原则是,
从上到下、从左到右断开代码的正常线性流,需要维护人员工作
更难理解的代码。为了承认这种额外的努力,认知
复杂性评估以下结构增量:
● Loop structures: for, while, do while, …
● Conditionals: ternary operators, if, #if, #ifdef, …
? 循环结构:for, while, do while, …
? 条件:三元运算符,if,#if,#ifdef,…
It assesses hybrid increments for:
它评估以下的混合增量:
● else if, elif, else, …
No nesting increment is assessed for these structures because the mental cost has already
been paid when reading the if.
对于这些结构,不会评估嵌套增量,因为心理成本已经
在读取 if 时已支付。
These increment targets will seem familiar to those who are used to Cyclomatic Complexity.
In addition, Cognitive Complexity also increments for:
这些增量目标对于习惯于循环复杂性的人来说似乎很熟悉。
此外,认知复杂性还增加了:
Catches
A catch represents a kind of branch in the control flow just as much as an if. Therefore,
each catch clause results in a structural increment to Cognitive Complexity. Note that a
catch only adds one point to the Cognitive Complexity score, no matter how many
exception types are caught. try and finally blocks are ignored altogether.
捕获异常
catch 表示控制流中的一种分支,就像 if 一样。因此
每个 catch 子句都会导致结构增量到认知复杂性。请注意,
catch 只增加了一个点的认知复杂性分数,无论多少
捕获异常类型。尝试,最后块被完全忽略。
Switches
A switch and all its cases combined incurs a single structural increment.
Under Cyclomatic Complexity, a switch is treated as an analog to an if-else if chain.
That is, each case in the switch causes an increment because it causes a branch in the
mathematical model of the control flow.
But from a maintainer’s point of view, a switch - which compares a single variable to an
explicitly named set of literal values - is much easier to understand than an if-else if
chain because the latter may make any number of comparisons, using any number of
variables and values.
In short, an if-else if chain must be read carefully, while a switch can often be taken
in at a glance.
开关
交换机及其所有案例组合会产生单个结构增量。
在循环复杂性下,交换机被视为 if-else 链的模拟。
也就是说,交换机中的每个情况都会导致增量,因为它会导致控制流的数学模型。
但从维护者的角度来看,一个开关 - 将单个变量与
显式命名的文本值集 - 比 if-else(如果链,因为后者可以作出任意数量的比较,使用任意数量的变量和值。
简而言之,如果链必须仔细阅读,而开关通常可以采取一目了然。
Sequences of logical operators
For similar reasons, Cognitive Complexity does not increment for each binary logical
operator. Instead, it assesses a fundamental increment for each sequence of binary logical
operators. For instance, consider the following pairs:
逻辑运算符序列
出于类似的原因,认知复杂性不会为每个二进制逻辑增加
算子。相反,它评估二进制逻辑的每个序列的基本增量
运营商。例如,请考虑以下对:
a && b
a && b && c && d
a || b
a || b || c || d
Understanding the second line in each pair isn’t that much harder than understanding the
first. On the other hand, there is a marked difference in the effort to understand the ollowing
two lines:
理解每对中的第二行并不像理解
第一。另一方面,在理解以下内容方面存在显著差异:
两行:
a && b && c && d
a || b && c || d
Because boolean expressions become more difficult to understand with mixed operators,
Cognitive complexity increments for each new sequence of like operators. For instance:
因为布尔表达式在混合运算符中越来越难以理解,
每个类似运算符的新序列的认知复杂性递增。例如:
if (a // +1 for `if`
&& b && c // +1
|| d || e // +1
&& f) // +1
if (a // +1 for `if`
&& // +1
!(b && c)) // +1
While Cognitive Complexity offers a “discount” for like operators relative to Cyclomatic
Complexity, it does increment for all sequences of binary boolean operators such as those in
variable assignments, method invocations, and return statements.
而认知复杂性为类似运营商提供了"折扣",相对于循环
复杂性,它确实增加所有序列的二进制布尔运算符,如那些
变量赋值、方法调用和返回语句。
Recursion
Unlike Cyclomatic Complexity, Cognitive Complexity adds a fundamental increment for each
method in a recursion cycle, whether direct or indirect. There are two motivations for this
decision. First, recursion represents a kind of “meta-loop”, and Cognitive Complexity
increments for loops. Second, Cognitive Complexity is about estimating the relative difficulty
of understanding the control flow of a method, and even some seasoned programmers find
recursion difficult to understand.
递 归
与循环复杂性不同,认知复杂性为每个
递归循环中的方法,无论是直接的还是间接的。有两个动机
决定。首先,递归代表一种"元循环",认知复杂性
循环的增量。其次,认知复杂性是估计相对难度
理解一个方法的控制流,甚至一些经验丰富的程序员发现
递归难以理解。
Jumps to labels
goto, and break or continue to a label add fundamental increments to Cognitive
Complexity. But because an early return can often make code much clearer, no other
jumps or early exits cause an increment.
跳转到标签
goto,并打破或继续一个标签添加基本增量认知
复杂性。但是,因为早期返回通常可以使代码更清晰,没有其他
跳转或提前退出会导致增加。
Increment for nested flow-break structures
It seems intuitively obvious that a linear series of five if and for structures would be easier
to understand than that same five structures successively nested, regardless of the number
of execution paths through each series. Because such nesting increases the mental
demands to understand the code, Cognitive Complexity assesses a nesting increment for it.
Specifically, each time a structure that causes a structural or hybrid increment is nested
inside another such structure, a nesting increment is added for each level of nesting. For
instance, in the following example, there is no nesting increment for the method itself or for
the try because neither structure results in either a structural or a hybrid increment:
嵌套流中断结构的增量
从直觉上讲,一个线性系列五如果和为结构将更容易
理解比相同的五个结构连续嵌套,无论数字
执行路径。"因为这样的嵌套增加了精神
需要理解代码,认知复杂性评估它的嵌套增量。
具体来说,每次嵌套导致结构或混合增量的结构时
在另一个此类结构中,为每个嵌套级别添加嵌套增量。对于
实例,在下面的示例中,该方法本身或
尝试,因为两个结构都会导致结构或混合增量:
void myMethod () {
try {
if (condition1) { // +1
for (int i = 0; i < 10; i++) { // +2 (nesting=1)
while (condition2) { … } // +3 (nesting=2)
}
}
} catch (ExcepType1 | ExcepType2 e) { // +1
if (condition2) { … } // +2 (nesting=1)
}
} // Cognitive Complexity 9
However, the if, for, while, and catch structures are all subject to both structural and
nesting increments.
但是,如果、同时和捕获结构都受结构和嵌套增量。
Additionally, while top-level methods are ignored, and there is no structural increment for
lambdas, nested methods, and similar features, such methods do increment the nesting
level when nested inside other method-like structures:
此外,当忽略顶级方法时,并且没有
lambdas、嵌套方法和类似的功能,这些方法确实会增加嵌套
当嵌套在其他类似方法的结构中时,级别:
void myMethod2 () {
Runnable r = () -> { // +0 (but nesting level is now 1)
if (condition1) { … } // +2 (nesting=1)
};
} // Cognitive Complexity 2
#if DEBUG // +1 for if
void myMethod2 () { // +0 (nesting level is still 0)
Runnable r = () -> { // +0 (but nesting level is now 1)
if (condition1) { … } // +3 (nesting=2)
};
} // Cognitive Complexity 4
#endif
The implications
Cognitive Complexity was formulated with the primary goal of calculating method scores that
more accurately reflect methods’ relative understandability, and with secondary goals of
addressing modern language constructs and producing metrics that are valuable above the
method level. Demonstrably, the goal of addressing modern language constructs has been
achieved. The other two goals are examined below.
影响
认知复杂性的制定与计算方法分数的首要目标:
更准确地反映方法的相对可理解性,并具有
解决现代语言构造,并生成在
方法级别。显然,解决现代语言结构的目标一直是
实现。下文将介绍其他两个目标。
Intuitively ‘right’ complexity scores
This discussion began with a pair of methods with equal Cyclomatic Complexity but
decidedly unequal understandability. Now it is time to re-examine those methods and
calculate their Cognitive Complexity scores:
直观的"正确"复杂性分数
此讨论开始与一对方法具有相等的循环复杂性,但
绝对不平等的理解性。现在是时候重新审视这些方法了,
计算他们的认知复杂性分数:
int sumOfPrimes(int max) {
int total = 0;
OUT: for (int i = 1; i <= max; ++i) { // +1
for (int j = 2; j < i; ++j) { // +2
if (i % j == 0) { // +3
continue OUT; // +1
}
}
total += i;
}
return total;
} // Cognitive Complexity 7
String getWords(int number) {
switch (number) { // +1
case 1:
return "one";
case 2:
return "a couple";
case 3:
return “a few”;
default:
return "lots";
}
} // Cognitive Complexity 1
The Cognitive Complexity algorithm gives these two methods markedly different scores,
ones that are far more reflective of their relative understandability.
认知复杂性算法给出的两种方法得分明显不同,
那些更能反映他们的相对可理解性。
Metrics that are valuable above the method level
Further, because Cognitive Complexity does not increment for the method structure,
aggregate numbers become useful. Now you can tell the difference between a domain class - one with a large number of simple getters and setters - and one that contains a complex
control flow by simply comparing their metric values. Cognitive Complexity thus becomes a
tool for measuring the relative understandability of classes and applications.
在方法级别之上有价值的指标
此外,由于方法结构的认知复杂性不会增加,
聚合数变得有用。现在,您可以分辨域类之间的区别- 一个与大量的简单获取器和设置器 - 一个包含一个复杂的控制流,只需比较其指标值。认知复杂性因此成为
用于测量类和应用程序的相对可理解性的工具。
Conclusion
The processes of writing and maintaining code are human processes. Their outputs must
adhere to mathematical models, but they do not fit into mathematical models themselves.
This is why mathematical models are inadequate to assess the effort they require.
Cognitive Complexity breaks from the practice of using mathematical models to assess
software maintainability. It starts from the precedents set by Cyclomatic Complexity, but
uses human judgment to assess how structures should be counted, and to decide what
should be added to the model as a whole. As a result, it yields method complexity scores
which strike programmers as fairer relative assessments of understandability than have
been available with previous models. Further, because Cognitive Complexity charges no
“cost of entry” for a method, it produces those fairer relative assessments not just at the
method level, but also at the class and application levels.
结论
编写和维护代码的过程是人类的过程。他们的产出必须坚持数学模型,但它们本身并不适合数学模型。
这就是为什么数学模型不足以评估它们需要的努力。
认知复杂性打破了使用数学模型进行评估的实践软件可维护性。它从循环复杂性开创的先例开始,但使用人类判断来评估结构应该如何计数,并决定什么应作为一个整体添加到模型中。因此,它产生方法复杂性分数罢工程序员作为更公平的相对评估的理解性比有
可用于以前的型号。此外,因为认知复杂性不收费
"输入成本"的方法,它产生那些更公平的相对评估,而不仅仅是在方法级别,但也在类和应用程序级别。
下面来点实战的代码,直观感受下怎么计算复杂度,以及怎么写出优秀的代码
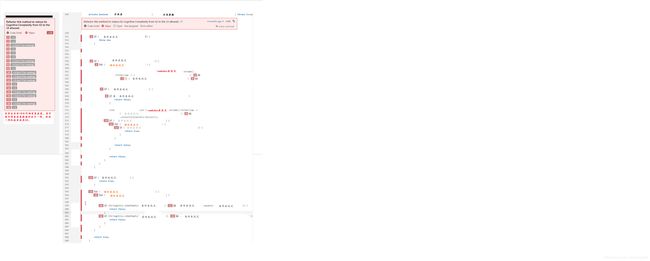
好好分析下这个图片的每一行代码,我把实际的实现删除了,剩下的代码都是存在复杂度问题,其余的行不会累加复杂度数。
这个方法总共有59行代码,其中有19行代码是由复杂度问题。
其中第12行的复杂度为6,它复杂度值最大, 它的层级是:2-3-7-10-11-12 ,嵌套了6层。
1.嵌套的代码会逐层增加复杂度数量,也就是说,在if或类for里面的代码,层级越深复杂度数会逐层递增1,这点非常重要
2.类if判断里面的逻辑表达式,也会增加1个复杂度
把握这两点你就能写出阅读性更好,复杂度更低,代码重用性更好的优秀代码。
怎么解决复杂度,提供思路:
1.一个大的方法进来拆成可复用的小方法,这点可以解决90%的问题。
2.尽量避免嵌套层级,不管是类if判断还是类for循环。