Machine Learning Course-CS 156 笔记 5

Lecture 5 : Training versus Testing

视频地址：https://www.youtube.com/watch?v=SEYAnnLazMU

---

测试与训练

用期末考试举例。
测试：

P[|Ein−Eout|>ϵ]≤2e−2ϵ2N P [ | E i n − E o u t | > ϵ ] ≤ 2 e − 2 ϵ 2 N

训练：

P[|Ein−Eout|>ϵ]≤2Me−2ϵ2N P [ | E i n − E o u t | > ϵ ] ≤ 2 M e − 2 ϵ 2 N

M M 从哪里来？
不好的事件 Bm B m 是 ’ |Ein−Eout|>ϵ | E i n − E o u t | > ϵ ‘

联合边界：

P[B1∪B2∪⋯∪BM]≤P[B1]+P[B2]+⋯+P[BM] P [ B 1 ∪ B 2 ∪ ⋯ ∪ B M ] ≤ P [ B 1 ] + P [ B 2 ] + ⋯ + P [ B M ]

可以在 M M 上进行改进吗？
不好的事件非常重叠。

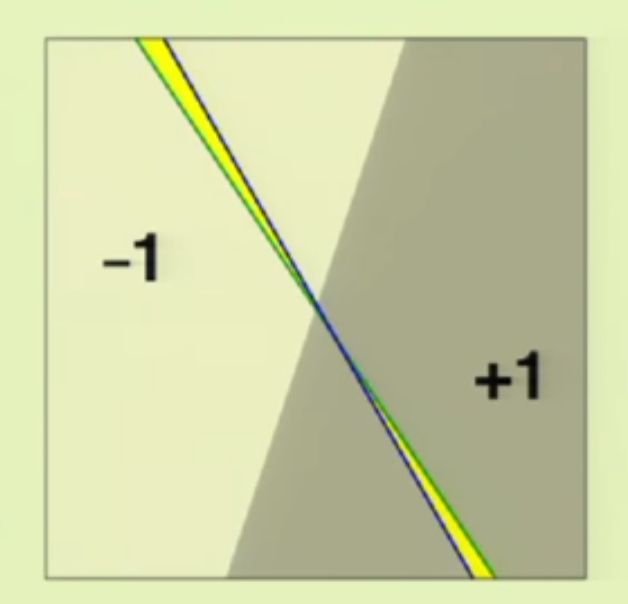
蓝线和绿线是两个分界面。

ΔEout:+1和−1区域的改变ΔEin:数据点标签的改变|Ein(h1)−Eout(h1)|≈|Ein(h2)−Eout(h2)| Δ E o u t : + 1 和 − 1 区 域 的 改 变 Δ E i n : 数 据 点 标 签 的 改 变 | E i n ( h 1 ) − E o u t ( h 1 ) | ≈ | E i n ( h 2 ) − E o u t ( h 2 ) |

替代 M M
用输入点的有限集合来替代所有的输入空间，并且计算二分法(假设)的数量

二分法：微型假设
一个假设 h:X→{−1,+1} h : X → { − 1 , + 1 }
一个二分 h:{x1,x2,⋯,xN}→{−1,+1} h : { x 1 , x 2 , ⋯ , x N } → { − 1 , + 1 }

假设集 |H| | H | 的数量无限的。
二分集合 |H(x1,x2,⋯,xN)| | H ( x 1 , x 2 , ⋯ , x N ) | 的数量最多为 2N 2 N

The growth function
计算了 N N 点上最多的二分集

mH(N)=maxx1,⋯,xN∈X|H(x1,⋯,xN)| m H ( N ) = max x 1 , ⋯ , x N ∈ X | H ( x 1 , ⋯ , x N ) |

growth function满足 : mH(N)≤2N m H ( N ) ≤ 2 N

• mH(3)=8 m H ( 3 ) = 8
• mH(4)=14 m H ( 4 ) = 14 (当+1点在对角线上时无法分割)

---

examples

1.射线

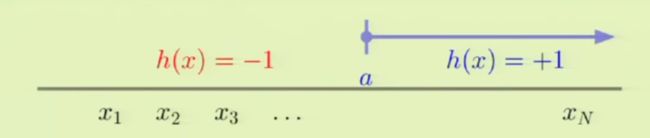
H是h:R→{−1,+1}的集合h(x)=sign(x−a)mH(N)=N+1 H 是 h : R → { − 1 , + 1 } 的 集 合 h ( x ) = s i g n ( x − a ) m H ( N ) = N + 1

2.区间

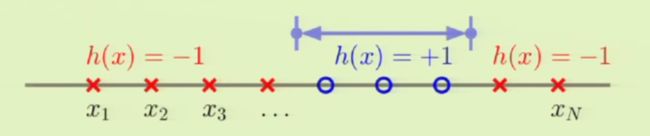
H是h:R→{−1,+1}的集合mH(N)=C2N+1+1=12N2+12N+1 H 是 h : R → { − 1 , + 1 } 的 集 合 m H ( N ) = C N + 1 2 + 1 = 1 2 N 2 + 1 2 N + 1

3.凸集

H是h:R2→{−1,+1}的集合mH(N)=2N H 是 h : R 2 → { − 1 , + 1 } 的 集 合 m H ( N ) = 2 N

根据下图理解：

N N 个点被凸集“shatter”了

当 mH(N) m H ( N ) 替代 M M 时会怎样？
只需证明 mH(N) m H ( N ) 是多项式

---

break point

定义： 如果没有大小为 k k 的数据集可以被 H H ‘shatter’,那么 k k 就是 H H 的一个break point

对于2维的感知机，break point是 k=4 k = 4

继续前面的例子：

• 对于射线 mH(N)=N+1 m H ( N ) = N + 1 , break point 是 k=2 k = 2
• 对于区间 mH(N)=12N2+12N+1 m H ( N ) = 1 2 N 2 + 1 2 N + 1 , break point 是 k=3 k = 3
• 对于凸集 mH(N)=2N m H ( N ) = 2 N , break point 是 k=∞ k = ∞

---

结论

没有break point ⟹mH(N)=2N ⟹ m H ( N ) = 2 N
有break point ⟹mH(N) ⟹ m H ( N ) 是 N N 的多项式