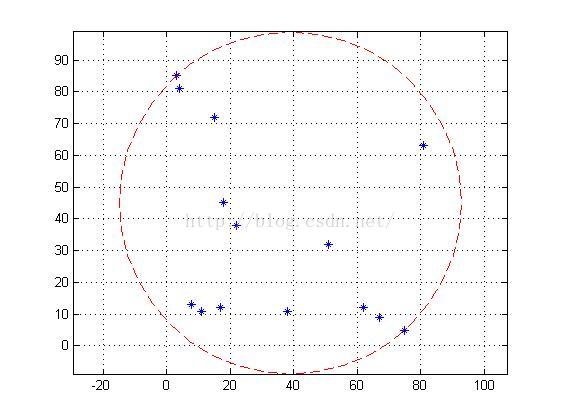
matlab 实现最小包围圆

最远点优先渐近算法：

2000年汪卫等提出一种准确且快速的点集最小包围圆算法，简记为DFAA。该算法的主要步聚是：

第一，在点集中任取3个点：A、B、C；

第二，以这3个点构造最小包围圆D；

第三，在点集P中查询距离D的圆心最远的点v；若v在D内则算法终止；否则，

第四，在｛A，B，C，v｝中选取3个点，构造包含4个点的最小包围圆D'，转第二步骤，基中选取的这3个点尽可能是边界上的点。

matlab 算法实现。代码包含两个M文件：minEncloseCircel.m 和 minCirclePoints3.m

minEncloseCircel.m:

clear all;close all;clc;

x=[22 8 4 51 38 17 81 18 62 15 11 3 75 67];
y=[38 13 81 32 11 12 63 45 12 72 11 85 5 9];
plot(x,y,'*');hold on;
grid on%
set_3P=nchoosek(1:length(x),3);
AI=set_3P(1,1);
BI=set_3P(1,2);
CI=set_3P(1,3);
A=[x(AI) y(AI)];
B=[x(BI) y(BI)];
C=[x(CI) y(CI)];
while 1
    R=minCirclePoints3(A,B,C);
    cr=[R(1),R(2)];
    r=zeros(1,length(x));
    for i=1:length(x)
       r(i)=sqrt((x(i)-cr(1))^2+(y(i)-cr(2))^2);
    end;
    maxValue=max(r);    %或者N=max(r(:))
    [mc]=find(maxValue==r);
    
    %没有点在圆外，或者最远点包含在A、B、C三点之中（精度误差导致），结束
    if maxValue <= R(3) || ~isempty( intersect(mc, [AI BI CI]) )
        alpha=0:pi/20:2*pi;%角度[0,2*pi]
        plot(cr(1)+R(3)*cos(alpha),cr(2)+R(3)*sin(alpha),'--r');%中心点在（R(1),R(2)）半径为R(3)的圆
        axis equal;
        break;%所有点都被圆覆盖       
    else
       %距离圆心最远的点在圆外       
    end;
    D=[x(mc),y(mc)];
    P=[A;B;C;D];%保存这四个点的坐标
     
    DI=mc;
    set_3P=nchoosek([AI,BI,CI,DI],3);
    rSet=[];
    for i=1:length(set_3P)
        A=[x(set_3P(i,1)) y(set_3P(i,1))];
        B=[x(set_3P(i,2)) y(set_3P(i,2))];
        C=[x(set_3P(i,3)) y(set_3P(i,3))];
        
        R=minCirclePoints3(A,B,C);
        rSet=[rSet;[R,i]];%每行：圆心坐标,半径,第几组(每组包括随机的三个点)
    end;
    rSet=sortrows(rSet,3);%按照半径排序
    
%   在四个圆中找一个最小半径圆包含这四个点
    for i=1:size(rSet,1)
        flag = 1;
        for j=1:4
          if sqrt((rSet(i,1)-(P(j,1) ))^2+ ( rSet(i,2)-(P(j,2)))^2) >rSet(i,3)%这个圆不行
            flag = 0; 
            break;
          end
        end;
        if flag == 1     %第i组三个点产生的圆可行--必然可以找到一个
            break;
        end;
    end;
    
    mc=rSet(i,4);
    AI = set_3P(mc, 1);
    BI = set_3P(mc, 2);
    CI = set_3P(mc, 3);
    A=[x(set_3P(mc,1)) y(set_3P(mc,1))];
    B=[x(set_3P(mc,2)) y(set_3P(mc,2))];
    C=[x(set_3P(mc,3)) y(set_3P(mc,3))];
end;

R  %显示结果

minCirclePoints3.m

function R=minCirclePoints3(A,B,C)
X=[A(1) B(1) C(1)];
Y=[A(2) B(2) C(2)];
%计算三边的长度AB BC CA
len=[sqrt((X(1)-X(2))^2+(Y(1)-Y(2))^2) sqrt((X(2)-X(3))^2+(Y(2)-Y(3))^2) sqrt((X(3)-X(1))^2+(Y(3)-Y(1))^2)];
%在非特殊情况下计算三角形三角的余弦值 cosA,cosB,cosC
if(sum(len>0)==3)
abc=[cosABC(len(2),len(1),len(3)) cosABC(len(3),len(1),len(2)) cosABC(len(1),len(2),len(3))];
end
%两点重合、三点重合、三点共线
if(len(1)==len(2)+len(3))
    r=len(1)/2;
    a=(X(1)+X(2))/2;
    b=(Y(1)+Y(2))/2;
    R=[a b r];
elseif(len(2)==len(1)+len(3))
    r=len(2)/2;
    a=(X(2)+X(3))/2;
    b=(Y(2)+Y(3))/2;
    R=[a b r];
elseif(len(3)==len(1)+len(2))
    r=len(3)/2;
    a=(X(1)+X(3))/2;
    b=(Y(1)+Y(3))/2;
    R=[a b r];
%--------------------------------------------------------------------------
else
    tmp=(abc<=0);
    if(tmp(1))
        r=len(2)/2;
        a=(X(2)+X(3))/2;
        b=(Y(2)+Y(3))/2;
        R=[a b r];
    elseif(tmp(2))
        r=len(3)/2;
        a=(X(1)+X(3))/2;
        b=(Y(1)+Y(3))/2;
        R=[a b r];
    elseif(tmp(3))
        r=len(1)/2;
        a=(X(1)+X(2))/2;
        b=(Y(1)+Y(2))/2;
        R=[a b r];
    elseif(sum(tmp)==0)
        a=(((X(1)^2-X(2)^2+Y(1)^2-Y(2)^2)*(Y(2)-Y(3)))-((X(2)^2-X(3)^2+Y(2)^2-Y(3)^2)*(Y(1)-Y(2))))/(2*(X(1)-X(2))*(Y(2)-Y(3))-2*(X(2)-X(3))*(Y(1)-Y(2)));
        b=(((X(1)^2-X(2)^2+Y(1)^2-Y(2)^2)*(X(2)-X(3)))-((X(2)^2-X(3)^2+Y(2)^2-Y(3)^2)*(X(1)-X(2))))/(2*(Y(1)-Y(2))*(X(2)-X(3))-2*(Y(2)-Y(3))*(X(1)-X(2)))  ;
        r=sqrt((X(1)-a)^2+(Y(1)-b)^2);
        R=[a b r];
    end
end
%d=linspace(0,2*pi,100);
%plot(a+r*sin(d),b+r*cos(d),'-',X(1),Y(1),'ro',X(2),Y(2),'bo',X(3),Y(3),'ko',a,b,'.')
%axis([0 10 0 10])
function c=cosABC(x,y,z)
c=(z^2+y^2-x^2)/(2*z*y);
end
end
 

运行结果：

R =
    39.0000   45.0000   53.8145

参考内容：

http://zhidao.baidu.com/link?url=al5bbjjKIXoEiRTqqqHMjHUIELTJEDqAG-vtgEFyKL6uD8mx9E0lYWewOY23XUB9hiRQP_41z55JEuyhS2KLda

《离散点最小包围圆算法分析与改进》--李红军