数据结构与算法－图的存储结构

图的存储结构分为邻接矩阵和邻接表两种。

邻接矩阵

1. 图的邻接矩阵

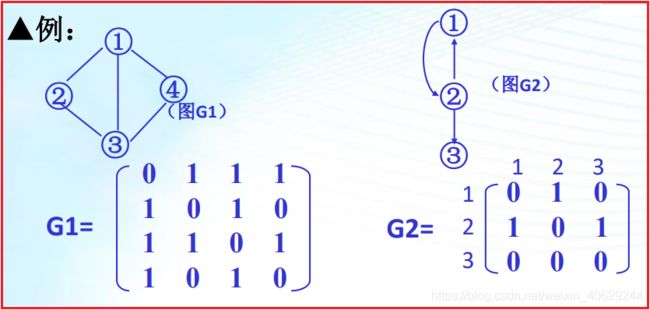
图的邻接矩阵为表示图的各顶点之间关系的矩阵。

设G=(V,E)是n个顶点的图，则G的邻接矩阵用n阶方阵G表示，若(Vi ,Vj )或< Vi ,Vj >属于E(G)，则G[i][j]为1，否则为0。

通过观察图与邻接矩阵的关系，我们可以得出以下结论。

1. 无向图的邻接矩阵是对称的。因为(Vi ,Vj )属于E(G)，则 (Vj ,Vi)亦属于E(G)。

2. 从邻接矩阵容易判断任意两顶点间是否有边相联， 容易求出各顶点的度。

(1). 无向图：顶点 Vi 的度D(Vi) 等于矩阵中第 i 行 或 第 j 列元素之和。如上图G1中顶点1的度为3。

(2). 有向图：OD(Vi) 等于矩阵中第 i 行元素之和，ID(Vi) 等于矩阵中第i列元素之和。如上图中G2中顶点3的出度为0，入度为1。

 

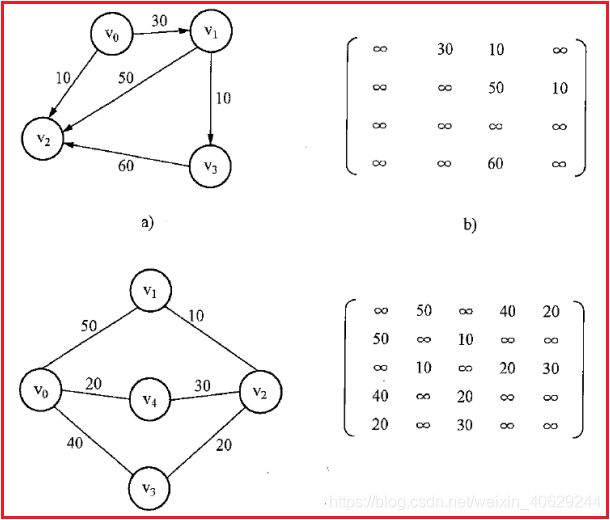
2. 带权图(网)的邻接矩阵

设G=(V,E)是n个顶点的图，则G的邻接矩阵用n阶方阵G表示，若(Vi ,Vj )或< Vi ,Vj > 属于 E(G)，则G[i][j]为边或弧的权Wij，否则Vi与Vj间无边或弧，用 ∞ 表示。

 

3. 邻接矩阵的类型定义

const int vnum=20;
typedef struct gp{ 
    // 顶点信息
    VertexType vexs[vnum]; 
    // 邻接矩阵
    WeightType arcs[vnum][vnum]; 
    // 顶点数，边数
    int vexnum,arcnum; 
}WGraph;

 

4. 建立无向带权邻接矩阵

实现步骤如下：

(1). 将矩阵A的每个元素都初始化为最大值。

(2). 然后读入边和权值（i，j，Wij），将A的相应 元素设为Wij，算法如下：

Void CreatGraph(Graph *g){ 
    int i,j,n,e,w;
    char ch;
    scanf("%d %d",&n,&e);
    g->vexnum=n;
    g->arcnum=e;
    for (i=0;ivexnum;i++){
        scanf("%c",&ch);
        g->vexs[i]=ch;
    };
    for (i=0;ivexnum;i++){
        for (j=0;jvexnum;j++){
            g->arcs[i][j]=MAX_INT
        }
    };
    for (k=0;karcnum;k++){
        scanf("%d %d %d",&i, &j,&w);
        g->arcs[i][j]=w;
        g->arcs[j][i]=w;
    }
}

 

邻接表

1. 邻接表的定义

邻接表是顺序存储与链式存储相结合的存储方法。

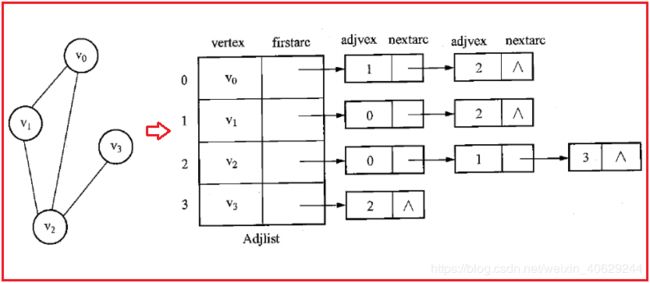
在邻接表中，对图中每个顶点建立一个单链表，每个单链表中链接图中与顶点相邻接的所有顶点。

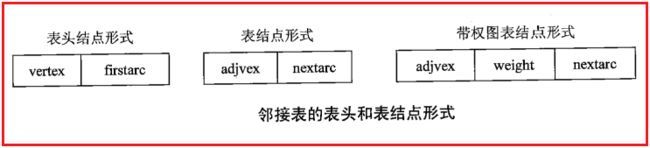
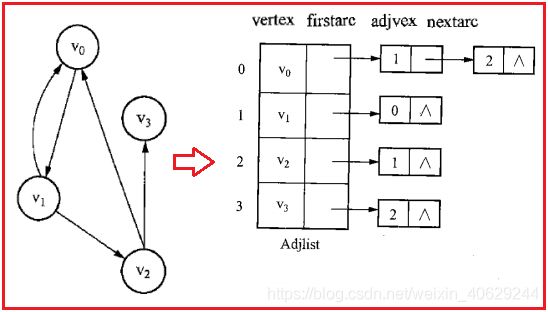
邻接表中的每个单链表均有一个表头结点，表头结点均含有两个域 ，一个是 vertex，用于存放当前顶点的信息，另一个是firstarc，用于指向邻接表中的第一个结点。

邻接表中的每个单链表含有不等个数的表结点，表结点含有两或三个域，一个是adjvex，存放与顶点相邻接顶点的序号，另一个是nextarc，指向该顶点的下一个邻接点，带权图表结点的形式还会多一个weight表示权重。

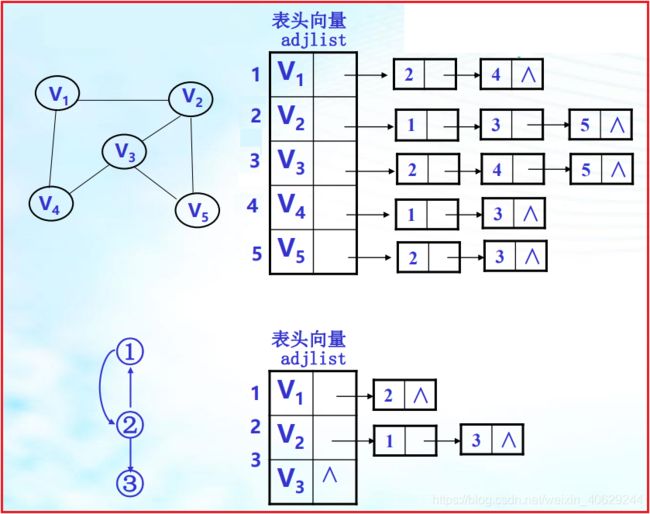
以下是无向图的邻接表示例。

 

以下是有向图的邻接表示例，每个单链表上记录是该顶点的出度。

对于有向图，有时需要建立一个逆邻接表，记录每个顶点相关联的入度。

 

2. 邻接表的特点

(1). n个顶点、e条边的无向图，则其邻接表的表头结点数为n， 链表结点总数为2e；

(2). 对于无向图，第i个链表的结点数为顶点Vi的度；对于有向图，第i个链表的结点数为顶点Vi的出度；

(3). 在边稀疏时，邻接表比邻接矩阵省单元；

(4). 邻接表表示在检测边数方面比邻接矩阵表示效率要高。

 

3. 计算图的度

(1). 对于无向图，第i个链表的结点数为顶点Vi的度；

(2). 对于有向图，第i个链表的结点数只为顶点Vi的出度；若要求入度， 必须遍历整个邻接表。在单链表中，其邻接点域的值为i的结点个数是顶点Vi的入度。

(3). 对于有向图，有时候就要建立一个邻接表。即队每个顶点Vi建立 一个以Vi为弧头的邻接点的链表。这样，逆邻接表第i个单链表中的 结点个数就是Vi的入度。

 

4. 带权图邻接表

带权图的邻接表中的结点包含一个权重域，如下所示。

以下是带权重的无向图的表现形式。

以下是带权重的有向图的表现形式。

 

5. 邻接表的类型定义

#define vnum 20
Typedef struct arcnode{ 
    // 下一条边的顶点编号
    int adjvex; 
    // 带权图的权值域
    WeightType weight; 
    // 指向下一条边的指针
    struct arcnode *nextarc;
}ArcNode;

Typedef struct vexnode{ 
    // 顶点编号
    int vertex; 
    // 指向第一条边的指针
    ArcNode *firstarc; 
}AdjList[vnum];

Typedef struct gp{ 
    AdjList adjlist;
    // 顶点和边的个数
    int vexnum,arcnum; 
}Graph;