操作系统实验3页面置换算法

地址映射过程中，若在页面中发现所要访问的页面不在内存中，则产生缺页中断。当发生缺页中断时，如果操作系统内存中没有空闲页面，则操作系统必须在内存选择一个页面将其移出内存，以便为即将调入的页面让出空间。而用来选择淘汰哪一页的规则叫做页面置换算法。

1．最佳置换算法（OPT）（理想置换算法）：从主存中移出永远不再需要的页面；如无这样的页面存在，则选择最长时间不需要访问的页面。于所选择的被淘汰页面将是以后永不使用的，或者是在最长时间内不再被访问的页面，这样可以保证获得最低的缺页率。

最佳置换算法可以用来评价其他算法。假定系统为某进程分配了三个物理块，并考虑有以下页面号引用串：
7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2, 1, 2, 0, 1, 7, 0, 1
进程运行时，先将7, 0, 1三个页面依次装入内存。进程要访问页面2时，产生缺页中断，根据最佳置换算法，选择第18次访问才需调入的页面7予以淘汰。然后，访问页面0时，因为已在内存中所以不必产生缺页中断。访问页面3时又会根据最佳置换算法将页面1淘汰……依此类推，如图3-26所示。从图中可以看出釆用最佳置换算法时的情况。

可以看到，发生缺页中断的次数为9，页面置换的次数为6。

2．先进先出置换算法（FIFO）：是最简单的页面置换算法。
这种算法的基本思想是：当需要淘汰一个页面时，总是选择驻留主存时间最长的页面进行淘汰，即先进入主存的页面先淘汰。其理由是：最早调入主存的页面不再被使用的可能性最大。

这里仍用上面的实例，釆用FIFO算法进行页面置换。进程访问页面2时，把最早进入内存的页面7换出。然后访问页面3时，再把2, 0, 1中最先进入内存的页换出。由图 3-27可以看出，利用FIFO算法时进行了 12次页面置换，比最佳置换算法正好多一倍。

FIFO算法还会产生当所分配的物理块数增大而页故障数不减反增的异常现象，这是由 Belady于1969年发现，故称为Belady异常，如图3-28所示。只有FIFO算法可能出现Belady 异常，而LRU和OPT算法永远不会出现Belady异常。
注意：内存的页面中“最老“的页面，会被新的网页直接覆盖，而不是“最老“的页面先出队，然后新的网页从队尾入队。

3．最近最久未使用（LRU）算法：这种算法的基本思想是：利用局部性原理，根据一个作业在执行过程中过去的页面访问历史来推测未来的行为。它认为过去一段时间里不曾被访问过的页面，在最近的将来可能也不会再被访问。所以，这种算法的实质是：当需要淘汰一个页面时，总是选择在最近一段时间内最久不用的页面予以淘汰。

再对上面的实例釆用LRU算法进行页面置换，如图3-29所示。进程第一次对页面2访问时，将最近最久未被访问的页面7置换出去。然后访问页面3时，将最近最久未使用的页面1换出。

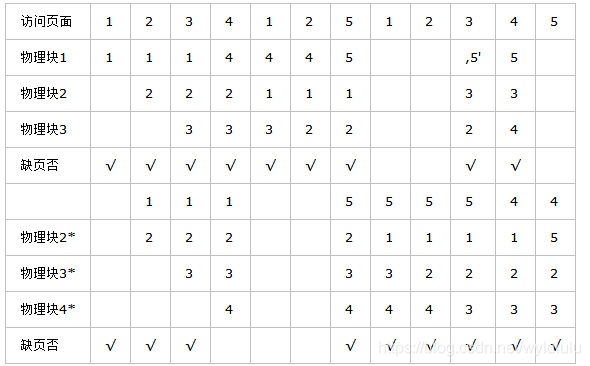
实际上，LRU算法根据各页以前的情况，是“向前看”的，而最佳置换算法则根据各页以后的使用情况，是“向后看”的。

LRU性能较好，但需要寄存器和栈的硬件支持。LRU是堆栈类的算法。理论上可以证明，堆栈类算法不可能出现Belady异常。FIFO算法基于队列实现，不是堆栈类算法。
C++代码实现：

#include 
using namespace std;
const int DataMax=100;
const int BlockNum = 10;
int DataShow[BlockNum][DataMax]; // 用于存储要显示的数组
bool DataShowEnable[BlockNum][DataMax]; // 用于存储数组中的数据是否需要显示
//int Data[DataMax]={4,3,2,1,4,3,5,4,3,2,1,5,6,2,3,7,1,2,6,1}; // 测试数据
//int N = 20; // 输入页面个数
int Data[DataMax]; // 保存数据
int Block[BlockNum]; // 物理块
int count[BlockNum]; // 计数器
int N ; // 页面个数
int M;//最小物理块数
int ChangeTimes;
void DataInput(); // 输入数据的函数
void DataOutput();
void FIFO(); // FIFO 函数
void Optimal(); // Optimal函数
void LRU(); // LRU函数

///*
int main(int argc, char* argv[])
{
   DataInput();//  DataInput();
  // FIFO();
  // Optimal();
 //  LRU();
 //  return 0;
      int menu;
	 while(true)
	 {
	   cout<>menu;

	   switch(menu)
	   {
	   case 1: FIFO();break;
	   case 2: Optimal();break;
	   case 3: LRU();break;
	   default: break;
	   }
	   if(menu!=1&&menu!=2&&menu!=3) break;
	 }
}
//*/
void DataInput()
{
 cout<<"请输入最小物理块数：";
 cin>>M;
 while(M > BlockNum) // 大于数据个数
 {
  cout<<"物理块数超过预定值，请重新输入：";
  cin>>M;
 }
 cout<<"请输入页面的个数：";
 cin>>N;
 while(N > DataMax) // 大于数据个数
 {
  cout<<"页面个数超过预定值，请重新输入：";
  cin>>N;
 }
 cout<<"请输入页面访问序列："<>Data[i];
}
void DataOutput()
{
 int i,j;
 for(i=0;i=3的块，替换后计数值置1，
       // 同时其它的块计数值加1 ，成了（1 3 2 ），见下面先进先出程序段
 }
 for(i=0;i M ) // 因为i是从0开始记，而M指的是个数，从1开始，所以i+1
  {
   //获得要替换的块指针
   temp = 0;
   for(j=0;j "<< endl;
 DataOutput();
}
void Optimal()
{
 int i,j,k;
 bool find;
 int point;
 int temp; // 临时变量，比较离的最远的时候用
 ChangeTimes = 0;
 for(j=0;j M ) // 因为i是从0开始记，而BlockNum指的是个数，从1开始，所以i+1
  {
   //获得要替换的块指针
   temp = 0;
   for(j=0;j "<< endl;
 DataOutput();
}
void LRU()
{
 int i,j;
 bool find;
 int point;
 int temp; // 临时变量
 ChangeTimes = 0;
 for(j=0;j M ) // 因为i是从0开始记，而BlockNum指的是个数，从1开始，所以i+1
  {
   //获得要替换的块指针
   temp = 0;
   for(j=0;j "<< endl;
 DataOutput();
}