图解散列表

引言

散列是一种用于以常数平均时间执行插入、删除和查找的技术。Java中HashMap就是基于它实现的。

原理

理想的散列表数据结构只是包含一些项(item)的具有固定大小的数组。而查找是对项的某个部分进行的，
这部分就叫关键字(key)。注意，关键字未必是可比较的。

散列表的大小记为TableSize，它也是散列数据结构的一部分。每个关键字(通过其hashcode/散列码/hash值)都被映射到从0到TableSize - 1这个范围
中的某个数。通常该数就是数组的索引，可以将项放到索引对应的位置。从关键字被映射到某个数叫作定址。
这个映射叫作散列函数。

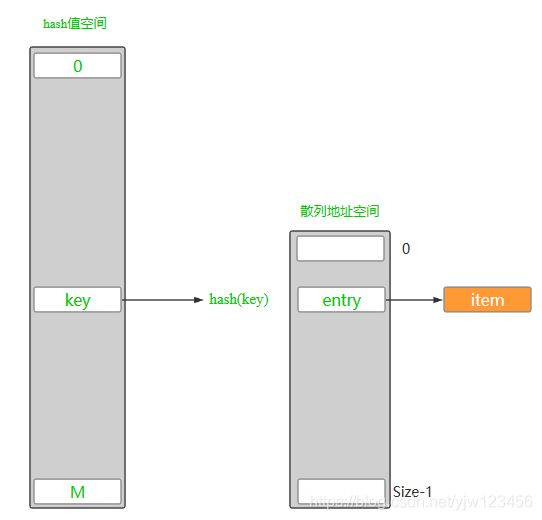
如上图所示，假定hash值最大为M，散列表大小为Size,M通常是远远大于Size的。
首先需要计算出key的hash值（一般通过key.hashCode()），然后经由散列函数进行定址。假设定到了entry这个地址，其指向的节点就是item。

这就是散列的基本思想，但是还有一个问题是，很有可能两个不同的key，经过hash操作都定位到同一个地址。这种情况叫做冲突。
因此，选择什么样的散列函数能尽可能的降低冲突，使表中的元素更分散以及如何解决冲突是我们接下来要探讨的问题。

散列函数

什么样的散列函数更好？ 需要根据散列函数的评价标准：

• 确定：同一关键码总是映射到同一地址
• 快速：计算必须要快速
• 满射：尽可能充分的覆盖整个散列空间(使表中的元素更分散)
• 均匀：关键码映射到散列表各位置的概率尽可能接近，要有效避免聚集现象（即都靠近某个位置，而其他位置少有问津）

取余法

常用的方法就是取余法：hash(key) = key % M

这种适用于关键字是整数，但表的大小需要仔细考虑。一般大小设置为素数，这样能尽可能保证分配均匀。

MAD法

取余法的缺点有：

• 不动点： 无论表长M取值如何，总有$hash(0)\equiv 0$
• 零阶均匀：相邻关键码的散列地址也比相邻

针对上述问题对取余法作出改进，引入MAD法(Multiply Add Divide)法：hash(key) = ( a * key + b) % M

M为素数，a > 0,b > 0,a % M <> 0

a相当于步长，b相当于偏移量。

多项式法

对于非数值key，首先就需要得到其hashcode。比如计算序列$s=A_0{A}_1...A_{n-1}$（如Java中的String）的hash值。

考虑下述算法(Horner法则)。计算$F(X)={\sum }_{i=0}^N{A}_i{X}^i$的值。

通过以下代码将公式中较为复杂的乘法计算，转换为简单的乘法与加法，其伪代码如下：

value = 0
for(i = N;i >= 0; i--)
	value = X * value + A[i]

其中，X取素数

我们就可以得到一个散列函数：

public static int hash(String key,int tableSize) {
	int hashVal = 0;
	for( int i = 0;i < key.length(); i++ ) {
		hashVal = 37 * hashVal + key.charAt(i);
	}
	hashVal %= tableSize;
	if(hashVal < 0 ) {
		hashVal += tableSize;
	}
	return hashVal;
}

该函数中X取37。

如果看过String的源码，可以看到类似的代码(经过了小小的修改)

public int hashCode() {
    int hash = 0;
    
    char val[] = value;//valule是 char数组(char[] value)

    for (int i = 0; i < value.length; i++) {
        hash  = 31 * hash  + val[i];
    }
    return hash;
}

冲突消除

剩下的主要问题就是冲突消除，如果某个元素被插入时与一个已经插入的元素散列到相同的值，
那么就产生一个冲突，这个冲突需要消除。常见的解决冲突的方法有：分离链接法和开放定址法。

分离链接法

将散列到同一个值的所有元素保留在一个链表中。
我们通过一个示例来说明，为了简单我们散列函数采用取余法，并将表大小设为10。
假定我们待插入的序列为：0,1,4,5,9,16,36,49

散列函数为：hash(x) = x mod 10

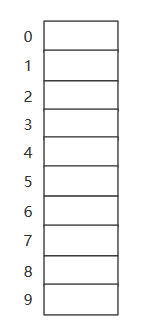
初始散列表如上图所示，然后我们依次插入

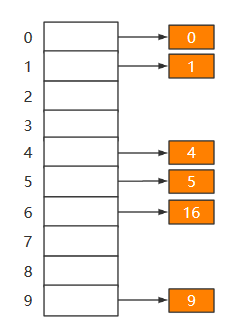
• 0 % 10 = 0;放到0位置
• 1 % 10 = 1;放到1位置
• 4 % 10 = 4;放到4位置
• 5 % 10 = 5;放到5位置
• 9 % 10 = 9;放到9位置
• 16 % 10 = 6;放到6位置

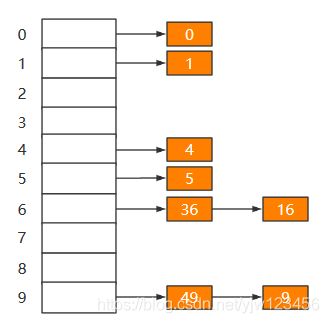
接下来36 % 10 = 6,放到6位置，但是6位置上已经有元素16了，根据分离链接法思想，采用头插法将36插入到6位置的链表中如下：

49也冲突了，采取同样的方式来处理

下面贴出该实现的代码:

package com.algorithms.hash;

import java.util.LinkedList;
import java.util.List;

/**
 * 分离链接法解决冲突的HashTable
 * 

 * 装填因子： 表中元素个数/表大小 ；在该实现类中为1
 *
 * @author yjw
 * @date 2019/5/6/006
 */
@SuppressWarnings("unchecked")
public class SeperateChainingHashTable<E> implements HashTable<E> {
    private List<E>[] lists;

    /**
     * 表中的元素数
     */
    private int size = 0;

    public SeperateChainingHashTable() {
        this(DEFAULT_TABLE_SIZE);
    }

    public SeperateChainingHashTable(int size) {
        //为了好计算hash值取素数
        lists = (List<E>[]) new LinkedList[nextPrime(size)];
        //初始化
        for (int i = 0; i < lists.length; i++) {
            lists[i] = new LinkedList<>();
        }
    }

    /**
     * 计算元素的hash值
     * @param x
     * @return
     */
    private int hash(E x) {
        int hashCode = x.hashCode();//得到对象的hash值
        hashCode %= lists.length;//通过取余法得到表中的位置
        if (hashCode < 0) {
            hashCode += lists.length;
        }
        return hashCode;
    }




    @Override
    public void insert(E x) {
        List<E> list = getOpList(x);
        if (!list.contains(x)) {
            list.add(0,x);//头插法
            if (++size > lists.length) {
                rehash();
            }
        }
    }

    /**
     * 扩容，并重新计算hash值，填充数据
     */
    private void rehash() {
        System.out.println("size:" + size + " ,lists.length:" + lists.length);//log
        List<E>[] oldLists = lists;//指向原来的链表数组
        lists = new LinkedList[nextPrime(2 * oldLists.length)];//扩容
        for (int i = 0; i < lists.length; i++) {//重新初始化
            lists[i] = new LinkedList<>();
        }

        size = 0; //size清零

        //重新计算hash也就是取出老表中的元素不停的插入到新表，利用insert方法去计算新的hash值
        for (int i = 0; i < oldLists.length; i++) {
            //遍历每个链表
            for(E item : oldLists[i]) {
                //直接调用插入方法
                insert(item);
            }
        }
    }

    @Override
    public boolean contains(E x) {
        List<E> list = getOpList(x);
        return list.contains(x);
    }

    @Override
    public void makeEmpty() {
        for (List<E> list : lists) {
            list.clear();
        }
        size = 0;
    }

    @Override
    public void remove(E x) {
        List<E> list = getOpList(x);
        if (list.remove(x)) {
            size--;
        }
    }

    @Override
    public void print() {
        if (size == 0) {
            System.out.println("[]");
        }
        int index = 0;
        for (List<E> list : lists) {
            int i = 0;
            System.out.printf("%3d:",index);
            if (list.size() == 0) {
                System.out.print("[]");
            } else {
                for (E e : list) {
                    System.out.print("[" + e + "]");
                    if (i != list.size() - 1) {
                        System.out.print("->");
                    }
                    i++;
                }
            }
            System.out.println();
            index++;
        }
    }

    /**
     * 得到x的hash值对应的list
     * @param x
     * @return
     */
    private List<E> getOpList(E x) {
        return lists[hash(x)];
    }
}

HashTable接口的定义为:

**
 * Hash表公共接口
 *
 * @author yjw
 * @date 2019/5/6/006
 */
public interface HashTable<E> {
    int DEFAULT_TABLE_SIZE = 101;

    void insert(E x);

    boolean contains(E x);

    void makeEmpty();

    void remove(E x);

    void print();

    /**
     * 获取比n大的最小素数
     *
     * @param n
     * @return
     */
    default int nextPrime(int n) {
        if (n % 2 == 0) {
            n++;
        }
        while (!isPrime(n)) {
            n += 2;
        }
        return n;
    }

    /**
     * 判断n是否是素数
     * @param n
     * @return
     */
    default boolean isPrime(int n) {
        if (n == 2 || n == 3) {
            return true;
        }
        if (n == 1 || n % 2 == 0) {
            return false;
        }

        for (int i = 3; i * i <= n; i += 2) {
            if (n % i == 0) {
                return false;
            }

        }
        return true;
    }

}

我们定义散列表的装填因子(load factor)$\lambda$为散列表中元素个数对该表大小的比值。
在上面的例子中，装填因子为1。链表的平均长度为$\lambda$。

执行一次查找所需要的工作是计算散列函数值所需的常数时间加上遍历链表所用的时间。
在一次不成功的查找中，要考查的节点数平均为$\lambda$。一次成功的查找则需要遍历大约$1+\frac{\lambda }{2}$个链。

开方定址法

当发生冲突时，使用某种探测技术在Hash表中形成一个探测序列，然后沿着这个探测序列依次查找下去，直到找出空单元为止。
探测序列单元：$h_0(x),h_1(x),h_2(x),...$的公式为：$h_i(x)=(hash(x)+f(i))\mathrm{m}\mathrm{o}\mathrm{d}TableSize$ ,且$f(0)=0$,$i=(0,1,2...)$
函数$f$是冲突解决方法，TableSize为表长。
现在我们来学习常见的冲突解决方案。

线性探测:

线性探测中$f(i)=i$，相当于相继探测逐个单元以查找出一个空单元。
下图显示使用与前面相同的散列函数将各个元素{89,18,49,58,69}加入到散列表中的情况：

索引	空表	插入89	插入18	插入49	插入58	插入69
0				49	49	49
1					58	58
2						69
3
4
5
6
7
8			18	18	18	18
9		89	89	89	89	89

从左往右看，首先是空表，然后是插入89后…

第一个冲突在插入49时产生；它被放入了下一个空闲地址，即0，该地址是开放的。
关键字58先与18冲突，再与89冲突，然后又和49冲突，试选3次后才得到一个空单元。
对于69的冲突采用类似的方法处理，只要表足够大，总能找到一个空单元。但是花费的
时间是相当多的，而且即使表相对较空，占据的单元也会形成一些块区。会造成元素聚集现象。

平方探测：

平方探测是消除线性探测中元素聚集问题的冲突解决方法。通常的选择是$f(i)=i^2$。下图显示与前面
线性探测例子相同的输入使用该冲突函数所得到的的散列表。

索引	空表	插入89	插入18	插入49	插入58	插入69
0				49	49	49
1
2					58	58
3						69
4
5
6
7
8			18	18	18	18
9		89	89	89	89	89

当49与89冲突时，其下一个位置$h_1(x)=1^2$ 也就是下一个单元，该单元(循环到0的位置，可以想象成一个环)是空的，插入。
此后，58在位置8处产生冲突，下一个位置89冲突，再下一个位置为$h_2(x)=2^2$为4， ( 8+4) % 10 = 2,是空的，插入。
对于69处理的过程也一样。

如果使用平方探测，且表的大小是素数，那么当表至少有一半是空的时候，总能插入一个新的元素。

另外，在探测散列表中标准的删除操作不能执行，因为相应的单元可能已经引起过冲突，元素绕过它存在了别处。因此，探测散列表需要懒惰删除——其实类似逻辑删除。

代码如下：

package com.algorithms.hash;

/**
 * 使用单向平方探测法来解决冲突
 *
 * @author yjw
 * @date 2019/5/7/007
 */
@SuppressWarnings("unchecked")
public class QuadraticProbingHashTable<E> implements HashTable<E> {
    private HashEntry<E>[] items;

    /**
     * 集合中元素数量
     */
    private int size;

    public QuadraticProbingHashTable() {
        this(DEFAULT_TABLE_SIZE);
    }

    public QuadraticProbingHashTable(int size) {
        allocate(size);
        makeEmpty();
    }

    /**
     * 为items分配空间
     *
     * @param n
     */
    private void allocate(int n) {
        size = 0;
        items = new HashEntry[nextPrime(n)];
    }

    public E find(E e) {
        int pos = findPos(e);
        return isActive(pos) ? items[pos].data : null;
    }


    @Override
    public void insert(E x) {
        int pos = findPos(x);
        if (!isActive(pos)) {
            items[pos] = new HashEntry<>(x);
            size++;
            if (size > items.length / 2) { //装填因子为0.5
                rehash();
            }
        }
    }

    private void rehash() {
        HashEntry<E>[] oldItems = items;
        allocate(2 * oldItems.length);
        for (int i = 0; i < oldItems.length; i++) {
            if (oldItems[i] != null && oldItems[i].active) {
                insert(oldItems[i].data);
            }
        }
    }

    @Override
    public boolean contains(E x) {
        int pos = findPos(x);
        return isActive(pos);
    }

    @Override
    public void makeEmpty() {
        size = 0;
        for (int i = 0; i < items.length; i++) {
            items[i] = null;
        }
    }

    @Override
    public void remove(E x) {
        int pos = findPos(x);
        if (isActive(pos)) {
            items[pos].active = false;
            --size;
        }
    }

    /**
     * 返回pos处的元素是否有效
     *
     * @param pos
     * @return
     */
    private boolean isActive(int pos) {
        return items[pos] != null && items[pos].active;
    }

    private int findPos(E x) {
        int offset = 1;
        int pos = hash(x);

        while (items[pos] != null && !items[pos].data.equals(x)) {
            /**
             * 进行平方探测的快速方法
             */
            pos += offset;
            offset += 2;
            pos = pos % items.length;
        }
        return pos;
    }

    private int hash(E x) {
        int hashCode = x.hashCode();
        hashCode %= items.length;
        if (hashCode < 0) {
            hashCode += items.length;
        }
        return hashCode;
    }

    @Override
    public void print() {
        if (size == 0) {
            System.out.println("[]");
            return;
        }
        for (int i = 0; i < items.length; i++) {
            System.out.printf("%3d",i);
            System.out.print(":[");
            if (items[i] != null && items[i].active) {
                System.out.print(items[i]);
            }
            System.out.println("]");
        }
    }

    /**
     * 带有删除标记的节点
     *
     * @param 
     */
    private static class HashEntry<E> {
        E data;
        /**
         * 是否激活,false表示已被删除
         */
        boolean active;

        public HashEntry(E e) {
            this(e, true);
        }

        public HashEntry(E e, boolean i) {
            data = e;
            active = i;
        }

        @Override
        public String toString() {
            return data + "";
        }
    }
}

另外附上测试代码：

@Test
public void testHashTable() {
    HashTable<String> hashTable = new SeperateChainingHashTable<>(10);
    String[] array = ("Norah Morahan O’Donnell is an American print and television journalist, currently " +
            "serving as the co-anchor of CBS This Morning. She is the former Chief White House Correspondent" +
            " for CBS News and the substitute host for CBS's Sunday morning show Face the Nation").split("\\W+");
    for (String s : array) {
        hashTable.insert(s);
    }
    System.out.println(hashTable.contains("host"));

    hashTable.print();
}

分离链接法的输出如下：

true
  0:[]
  1:[and]
  2:[]
  3:[]
  4:[show]
  5:[]
  6:[]
  7:[]
  8:[Sunday]
  9:[]
 10:[for]->[anchor]
 11:[CBS]
 12:[]
 13:[]
 14:[serving]
 15:[House]->[an]
 16:[]
 17:[Face]->[former]
 18:[of]
 19:[White]
 20:[host]->[as]
 21:[s]->[News]
 22:[Norah]
 23:[Nation]->[journalist]
 24:[]
 25:[]
 26:[]
 27:[the]
 28:[]
 29:[Correspondent]
 30:[]
 31:[This]->[television]->[co]
 32:[O]
 33:[is]
 34:[Donnell]
 35:[]
 36:[currently]
 37:[]
 38:[]
 39:[substitute]->[She]
 40:[morning]->[print]->[Morning]
 41:[Chief]->[American]
 42:[]
 43:[Morahan]
 44:[]
 45:[]
 46:[]