【Verilog HDL 训练】第 01 天

1. bit, byte, word, dword, qword的区别 ？

---

1 qword = 4 word;

1 dword = 2 word;

1 word = 2 byte;

1 byte = 8 bit;

百度百科的解释：

qword

1个二进制位称为1个bit，8个二进制位称为1个Byte，也就是1个字节（8位），2个字节就是1个Word（1个字，16位)，q就是英文quad-这个词根(意思是4)的首字母，就是一个word的4倍。所以它自然是word(2字节，0~2^16-1)的四倍，8字节，0~2^64-1)

凡是带word的(比如dword(4字节，0~2^32),qword)，都是非负数，一般在0 .. 18446744073709551615之间。

---

2. 什么是原码，反码，补码，符号-数值码。以8bit为例，给出各自表示的数值范围。

---

原码：

原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:

[+1]原 = 0000 0001

[-1]原 = 1000 0001

第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:

[1111 1111 , 0111 1111]

即

[-127 , 127]

反码：

反码的表示方法是:

正数的反码是其本身

负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.

[+1] = [00000001]原 = [00000001]反

[-1] = [10000001]原 = [11111110]反

可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算.

由于每一个数都有其对应的反码，所以反码表示的数的范围也为：[-127 , 127]

补码：

补码的表示方法是:

正数的补码就是其本身

负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)

[+1] = [00000001]原 = [00000001]反 = [00000001]补

[-1] = [10000001]原 = [11111110]反 = [11111111]补

对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码在计算其数值.

由于+0与-0对应同一个补码0000_0000，故编码1000_0000可表示-128，故补码的取值范围是：[-128~127]

总结：

补码能表示的有符号数的范围是.

参考链接：【 数字信号处理 】定点数的表示之二进制数的原码与补码

原码, 反码, 补码 详解

---

3. 十进制转换为二进制编码： 127， （-127），127.375，（-127.375）

---

十进制数转换为二进制数时，由于整数和小数的转换方法不同，所以先将十进制数的整数部分和小数部分分别转换后，再加以合并。

十进制整数转换为二进制整数采用"除2取余，逆序排列"法。

具体做法是：用2整除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为小于1时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。

故：127可以转换为二进制0111_1111

（-127）D=(1111_1111)原码=（1000_0000）反码=（1000_0001）补码

负数一般用补码表示，所以最终为（-127）D=（1000_0001）B

十进制小数转换成二进制小数采用"乘2取整，顺序排列"法。

具体做法是：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，此时0或1为二进制的最后一位。或者达到所要求的精度为止。

然后把取出的整数部分按顺序排列起来，先取的整数作为二进制小数的高位有效位，后取的整数作为低位有效位。

0.375*2=0.75     取0

0.75*2=1.5         取1

0.5*2 = 1            取1

故0.375对应的二进制为：0.011

127.375对应的二进制为：01111_1111.011

（-127.375） 对应的二进制是什么呢？

见链接：负小数如何用二进制表示？

浮点数在计算机中用原码表示，故（-127.375）=（1111_1111.011）

参考链接： 

https://zhidao.baidu.com/question/117636295.html

https://baike.baidu.com/item/%E5%8D%81%E8%BF%9B%E5%88%B6%E8%BD%AC%E4%BA%8C%E8%BF%9B%E5%88%B6

---

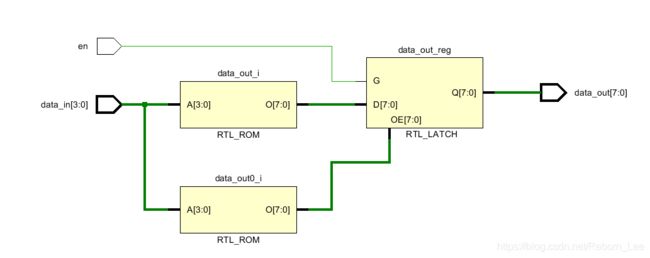
4. 设计BCD译码器，输入0~9。采用verilog描述并画出门级电路图。

---

`timescale 1ns / 1ps
//
// Company: 
// Engineer: 
// 
// Create Date: 2019/04/22 18:25:41
// Design Name: 
// Module Name: bcd_encoder
// 
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
// 共阳极数码管
//




module bcd_encoder(
	input en,
	input [3:0] data_in,
	output reg [7:0] data_out

);
	always@(*) begin
		if(en) begin
			case(data_in)
				4'b0000: begin
					data_out = 8'h3f;
				end
				4'b0001: begin
					data_out = 8'h06;
				end
				4'b0010: begin
					data_out = 8'h5b;
				end
				4'b0011: begin
					data_out = 8'h4f;
				end
				4'b0100: begin
					data_out = 8'h66;
				end
				4'b0101: begin
					data_out = 8'h6d;
				end
				4'b0110: begin
					data_out = 8'h7d;
				end
				4'b0111: begin
					data_out = 8'h07;
				end
				4'b1000: begin
					data_out = 8'h7f;
				end
				4'b1001: begin
					data_out = 8'h6f;
				end
				default: begin
					data_out = 8'hzz;
				end
			
			endcase
		
		end
		else ;
	end



endmodule

 

 

---

5. 异步FIFO深度为17，如何设计地址格雷码？

---

稍后！暂时未解决。

https://www.embedded.com/print/4015117