（算法竞赛）简单易懂二分图

今天本来想整理\(Kruskal\)算法和次小生成树的求解方法的，但是介于被一个求最大独立集的gou题卡了将近\(5\)个小时，所以决定先整理一下二分图的知识

FBI Warning：本篇博客极其哲学，不喜勿喷谢谢您的配合

Part 1：二分图的定义及判定

给出定义：

二分图又称作二部图，是图论中的一种特殊模型。 设\(G=(V,E)\)是一个无向图，如果顶点\(V\)可分割为两个互不相交的子集\((A,B)\)，并且图中的每条边\(（i，j）\)所关联的两个顶点\(i\)和\(j\)分别属于这两个不同的顶点集\((i \in A,j \in B)\)，则称图\(G\)为一个二分图。
——来自百度百科

百度百科的解释依旧很诡异，我们用图+文字来具体的描述一下（灵魂画师请战）：

现在给出这样的一张\(4\)个点\(4\)条边的无向图：

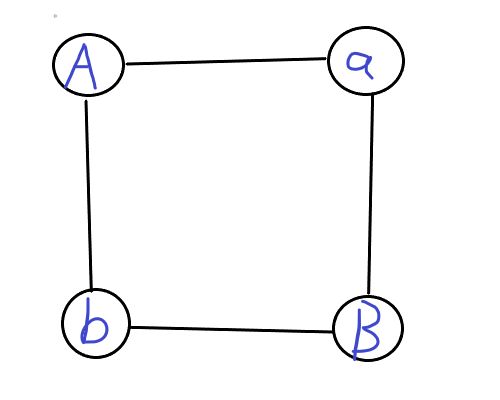
我们交换\(B\)和\(b\)的位置，重新把这个图画一遍：

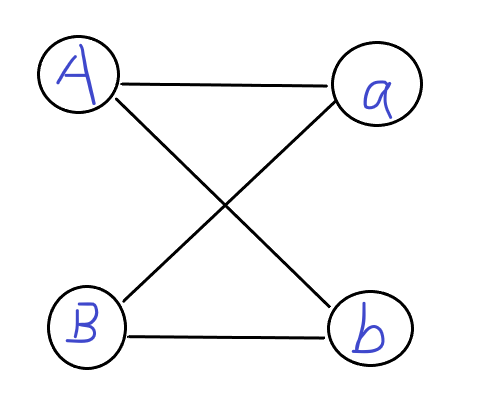
可以发现，这个图现在被我们划分成了左边（\(A、B\)）和右边（\(a、b\)）两部分

而且这两部分满足这样的性质：同属左边或右边的点之间没有边相连

只要一个无向图被划分成左右两部分之后，可以满足上述条件，那么这张图就是一个二分图

现在给出更加一般且方便的二分图判定法则：

定理：假设每条边的长度为\(1\)，如果一个无向图中没有长度为奇数的环，那么这个图就是一张二分图

警告：以下的证明作者几乎都在扯\(dan\)，如果您想更快的学习二分图的知识，请直接跳过证明部分

我们来尝试感性的证明一下这个定理

开始证明

用黑白染色法来区分开左右的点，一开始，所有的点都没有被染色（设左边的点都是黑色，右边的点都是白色）
还是\(（1\rightarrow 2\rightarrow 3\rightarrow 1）\)的奇环，不妨设\(1\)是黑色，如果这是一张二分图，那么\(2\)与\(1\)相连，\(2\)应该为白色，\(2\)与\(3\)相连，\(3\)应该为黑色，\(1\)与\(3\)相连，\(1\)应该是白色，这显然与一开始的假设（\(1\)是黑色）矛盾了，所以“这是一张二分图”的假设不成立，故这不是一张二分图
那么现在，我们把长度为\(3\)这个假设去掉，改成存在长度为\(x\)（\(x\)%\(2=1\))的环
我们先把\(1\)号点和\(x\)号点之间的边断开，单纯的研究这一条链：
不妨设\(1\)号点是黑色，如果想要满足二分图的性质，相邻点的颜色必须不同，那么\(2\)是白色，以此类推：\(3\)黑，\(4\)白，\(5\)黑……
继而很简单的可以推出：编号为奇数的点一定都是黑色，编号为偶数的点一定都是白色，那么\(x\)号点一定是黑色（因为\(x\)是奇数）
但是不要忘了，\(x\)号点和\(1\)号点有一条边相连，此时\(x\)号点和\(1\)号点都是黑色且有边相连，显然不满足二分图的性质，所以如果存在奇数环的图，一定不是二分图
那么对于偶环呢？显然偶环的最后一个点和第一个点的颜色不同，所以一张图存不存在偶环对于这张图是不是二分图并没有影响
对于链就更没有影响了：只要一个放左边一个放右边一直放下去直到放完整条链就\(OK\)了
众所周知，一张图一定是由环和链构成的，然后我们把这三种情况全都讨论了一遍，发现一张图是不是二分图仅与这张图中有没有奇环有关
那么证毕：当且仅当一张图中没有奇环时，无向图是一张二分图
以上证明全部是作者\(yy\)上去的，没有任何科学依据，仅供方便读者理解！！！

证毕

Part 2：二分图上的一些\(knowledge\)（定义）

现在我们来康康关于二分图还有什么其他刺激的知识：

\(1、\)最大匹配

定义：在二分图\(G\)的一个子图\(M\)中，\(M\)的边集中的任意两条边都不依附于同一个顶点，则称\(M\)是一个匹配。选择这样的边数最大的子集称为图的最大匹配问题,最大匹配的边数称为最大匹配数

按照作者的尿性，我们要用通俗易懂的语言化简一下复杂的定义，我们用一个妙趣横生的故事，来帮助理解和记忆

今年是公元\(2050\)年，为了帮助更多的单身人士脱单，\(Z\)国决定组织一场全国性的相亲大会，而你被当选为大会的主办人

现在我们有\(n\)位男嘉宾（左边）和\(m\)位女嘉宾（右边），他们之间有\(k\)个互相中意的关系（边）（这就是一张二分图了）

但是\(Z\)国人非常的有追求和理想，当且仅当男女嘉宾互相中意时，他们才能结对（只有左边节点和右边节点右边相连时，才能结对）

并且\(Z\)国的法律不允许“一夫多妻”或者“一妻多夫”，所以一位男嘉宾只能和一位女嘉宾匹配，反之亦然

国家主席布里jiojio邓布利多先生对国家的生育率表示担忧，所以他希望你能撮合出最多的情侣来

现在这个“最多的情侣数”就是“二分图最大匹配”数了，如果把定义套到情境里去，那么它就变成了这样：

使用\(k\)个关系，联系男生和女生，在不出现一个人和多个异性联系的情况下，使得联系对数最多。此时这个最多的对数，就是二分图最大匹配数

\(2、\)最小点覆盖

定义：最小点覆盖是指用最少的顶点数使得二分图\(G\)中的每条边都至少与其中一个点相关联

其实这个定义已经很好理解了，如果理解不了，那就又到了讲故事时间

在\(XX\)中学\(Z\)班中，出现了谈恋爱的不良风气！现在班主任布里jiojio邓布利多先生已经掌握了情报，他发现这些谈恋爱的学生可以组成这样的关系网：

其中有\(n\)个男生（左边\(n\)个点），\(m\)个女生（右边\(m\)个点），\(k\)对恋爱关系（边），并且让人作呕的是，有些同学与多个异性保持了恋爱关系！

现在布里jiojio邓布利多先生希望把这些谈恋爱的学生一网打尽，整顿班级风气，但是因为还有别的班级事务要管理，他决定对于每一对情侣，仅找其中的一方谈话教育

按道理来说，他需要谈话\(\frac{k}{2}\)次，但是因为有些同学与多个异性保持了恋爱关系！，所以实际上他并不需要进行那么多次谈话

时间紧迫，他需要你帮助他求出，他最少要谈话多少次才能保证这些情侣中的每一对中至少有一个人被谈话

现在把定义引申到情境中，它是这样的：

寻找一个点集\(S\)（谈恋爱的同学），使得图中去掉与点集\(S\)中的元素相连的边（谈话后破坏关系）之后，一条边也不剩（肃清班风），目标是：最小化点集\(S\)包含的元素个数

\(3、\)最小边覆盖

定义：用尽量少的不相交简单路径覆盖二分图中的所有顶点

这个定义稍微有点难理解，所以是讲故事时间

让我们回到第一个情景：国家主席布里jiojio邓布利多先生对于相亲大会的成果并不满意，在你向他说明情况后，他决定修改本国宪法

现在，\(Z\)国的宪法允许一夫多妻和一妻多夫制，现在，主席要求你帮所有人找到心仪的（有边相连的才算“心仪”）对象

就是在相亲大会上，当大部分人都得到了理想的匹配之后，总有一些人无法匹配（让我们假设其中的一名男性同胞叫做小\(A\)）

怎么办呢？小\(A\)并不想单身啊\(QAQ\)可是他喜欢的小姐姐已经有男朋友小\(B\)了！这时候你过来了，你让小\(A\)与小\(B\)都当小姐姐的男朋友

于是问题圆满地解决了，所有人都找到了心仪的对象（滑稽）

但是这还没完，你发现，如果一夫多妻或一妻多夫的人数太多，会导致人事纠纷，所以你想让这种关系的人数尽可能少

现在使得这种关系的人数最少的解，就是二分图最小边覆盖问题的解，用自己的话说定义就是：

定义：在所有点都找到匹配（找到心仪对象）的前提下，使得一个点匹配多个点（一夫多妻或一妻多夫）的情况数最少

\(4、\)最大独立集

定义：最大独立集是指寻找一个包含元素最多的点集，使得其中任意两点在图中无对应边

这个定义真的很好理解了，连故事都不用讲（其实是作者想象力太差编不出来了）

就是选出最多的点，使得图中没有一条边直接连接这些点中的任何两个（我感觉反而说复杂了）

问题本质

上面叨叨了一大堆定义，难道我们对于每个定义都要设计一种算法来求吗？

显 然 不 可 能 ！

最小割定理：一个二分图中的最大匹配数=最小点覆盖数

没错上面叨叨的了一大顿的最小点覆盖和最大匹配就是一个相同的问题！

定理证明：

首先，最小点覆盖一定\(\geq\)最大匹配，因为假设最大匹配为\(n\)，那么我们就得到了\(n\)条互不相邻的边，光覆盖这些边就要用到\(n\)个点。
现在我们来思考为什么最小点覆盖一定\(\geq\)最大匹配。任何一种\(n\)个点的最小点覆盖，一定可以转化成一个\(n\)的最大匹配。
因为最小点覆盖中的每个点都能找到至少一条只有一个端点在点集中的边（如果找不到则说明该点所有的边的另外一个端点都被覆盖，所以该点则没必要被覆盖，和它在最小点集覆盖中相矛盾）
只要每个端点都选择一个这样的边，就必然能转化为一个匹配数与点集覆盖的点数相等的匹配方案。所以最大匹配至少为最小点集覆盖数，即最小点覆盖一定\(\geq\)最大匹配。综上，二者相等。

证毕

现在来看看剩下的最小边覆盖和最大独立集

最小边覆盖要求使得一个点匹配多个点的情况数最少，那么请感性理解一下：

感性证明

我们从定义出发考虑：最小边覆盖是怎么计算的？
当一个点没有得到匹配，我们强行给它匹配上（上面那个小\(A\)的情景），记操作次数\(+1\)，那么最小边覆盖就是使得所有点都匹配上的前提下，最少的操作次数
那么，既然只要一个点没有得到匹配，就要强行操作一次，我们很容易就想到，只要使得没有匹配上的人数最少不就行了吗？
显然这么做，我们求出的最小边覆盖应该等于没有匹配上的人数，要想使得没有匹配上的人数最少，只需要让匹配上的人数最多即可。
那么怎么求最多匹配呢？当然是二分图最大匹配。得出结论：最小边覆盖=二分图点数-最大匹配数

证毕

所以最小边覆盖实质上也是求最大匹配，再来看最大独立集

最大独立集要求求一个元素最多的点集，使得其中每两个点之间没有边直接相连。

感性证明

我们可以这么想：如果我把一个图的边全部干掉该多好！那样我的最大独立集就是\(n\)了！
突然想到最小点覆盖：寻找一个元素最少的点集\(S\)，使得图中去掉与点集\(S\)中的元素相连的边之后，一条边也不剩
去掉最少的点使得一条边也不剩哎！去掉的最少意味着剩下的最多，一条边也不剩意味着剩下的点两两之间没有边相连，就是最大独立集的定义
所以得出结论：最大独立集=点数-最小点覆盖，最小点覆盖=最大匹配，最大独立集=\(n\)-最大匹配

证毕

所以对于上面所有的\(4\)种问题，其本质都可以转化成求二分图最大匹配的问题

但是我猜大家第一次看的时候，都会觉得这是\(4\)个互相独立的问题，出题人更是会根据这个特性来出各种各样的毒瘤题目，所以如果见到二分图的题不要怕，弄清楚题目问的是这\(4\)个问题的哪一种，然后求出最大匹配即可！

Part 3：求解二分图最大匹配问题

染色建图

使用匈牙利（增广路）算法可以方便的求解最大匹配问题，但是在匈牙利（增广路）算法之前，得先学会判断和建立二分图。。。

前面我有提到过黑白染色法，我们判断和建立二分图都是使用这个方法

实现也很暴力，如果当前点是黑的，那么与这个点相连的点一定是白的，反之亦然,然后递归染色即可

如果碰到矛盾的情况（比如说上面的那个奇环）说明这个图不是二分图

当然了，给出的图不一定连通，所以我们要扫一遍所有点，如果当前点没有被染色，那么就以这个点为起点进行染色

\(Code\)

void paint(const int x,const int color){
	int y;
	col[x]=color;//表示第x个点的颜色
	for(unsigned int i=0;i

匈牙利（增广路）算法

这里我们抛开原理，只谈实现和运用

工作过程：
\(1、\)设集合\(S\)是空集，即所有边都是非匹配边
\(2、\)寻找增广路\(path\)，把路径上的所有边的匹配状态取反，得到一个更大的匹配\(S'\)。
\(3、\)重复第\(2\)步，直到图中不存在增广路
这个算法的关键在于如何找到一条增广路。匈牙利算法依次尝试给每一个左部节点\(x\)寻找一个匹配的右部节点\(y\)
右部点\(y\)可以与左部点\(x\)匹配，一定满足下面两种情况的一种：
\(1、\)\(y\)本身就是非匹配点，此时无向边\((x,y)\)本身就是非匹配边，自己构成一条长度为\(1\)的增广路
\(2、\)\(y\)已经与左部点\(x'\)匹配，但从\(x'\)出发能找到另一个\(y'\)与\(x'\)匹配，此时路径\(x~y~x'~y'\)为一条增广路
——《算法竞赛进阶指南》李煜东

但是显然李煜东大佬给的这个解释我看不懂，于是用一些奇怪的途径了解了匈牙利算法之后，我编了这样一个故事帮助理解：

还是相亲大会的情景，为了满足布里jiojio邓布利多主席的要求，你知道自己需要求出二分图最大匹配数，但是可惜的是你不知道怎么求

时间紧迫，你决定用自己的方法试一试

首先，你让所有男嘉宾站在了一起，女嘉宾站在了一起，也就是这样：（假设男左女右，黑线代表可以匹配，红线表示已经匹配）

你从左边的第一个点开始尝试给他们配对，首先是\(0\)号男嘉宾

\(0\)号说：“我只喜欢\(2\)号小姐姐！”然后你带着他去找\(2\)号，发现\(2\)号没有男朋友，于是你先给他们匹配上了

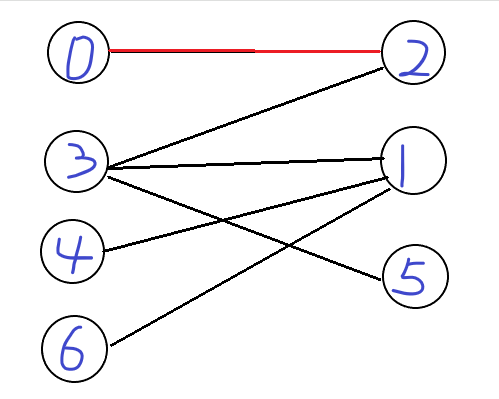
现在你去找第二个男嘉宾\(3\)号，\(3\)号说：“我也喜欢\(2\)号小姐姐”然后你带着他去找\(2\)号，发现\(2\)号已经有男朋友了，是刚才匹配的\(0\)号

你又带着\(3\)号去问\(0\)号：“你能不能换一个女朋友，然后把\(2\)号让给\(3\)号？”

但是\(0\)号除了跟\(2\)号有连线，就没有别的连线了，于是\(0\)号说：“不行我就只喜欢\(2\)号，我不干！”

没办法，你又问\(3\)号：“除了\(2\)号你还有喜欢的小姐姐吗？”\(3\)号说：“我觉得\(1\)号也挺好的”

于是你们去找\(1\)号，发现\(1\)号没有男朋友，所以\(3\)号和\(1\)号顺利匹配

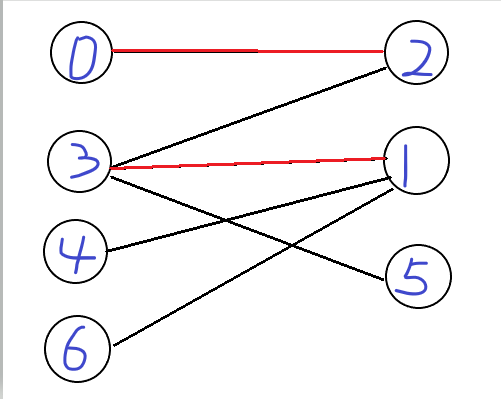
现在是第三个男嘉宾\(4\)号，\(4\)号说：“我喜欢\(1\)号！”

于是你们去找\(1\)号，\(1\)号有男朋友是\(3\)号。还是老套路，你去问\(3\)号能不能换女朋友，把\(1\)号让出来给\(4\)号

\(3\)号比较大方（花心）：“其实吧，\(5\)号人也挺好的。”然后\(3\)号去找\(5\)号，发现\(5\)号没有男朋友，于是\(3\)号和\(5\)号匹配，把\(1\)号让了出来

因为\(1\)号被\(3\)号让了出来，所以\(4\)号和\(1\)号成功匹配

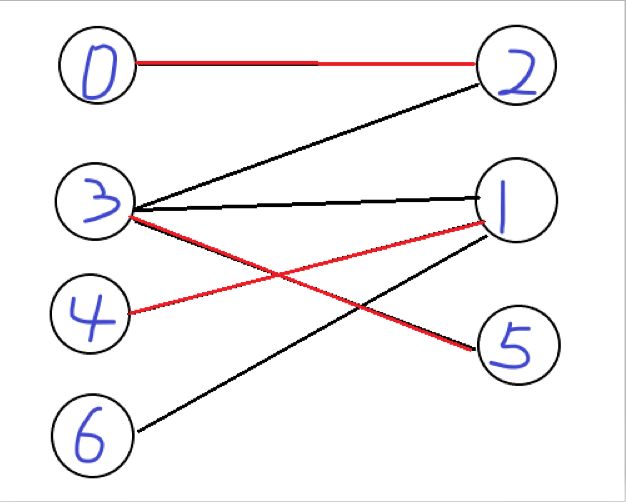
最后一个男嘉宾\(6\)号：“我喜欢\(1\)号！”于是你们去找\(1\)号，\(1\)号有男朋友是\(4\)号

老套路，你去问\(4\)号能不能换，把\(1\)号让出来给\(6\)号，可是\(4\)号除了和\(1\)号之外没有边了，他说：“不换不换！老子不换！说什么也不换！”

然而\(6\)号也只喜欢\(1\)号，但是因为先到先得，你只能遗憾的告诉\(6\)号他得孤独终老了

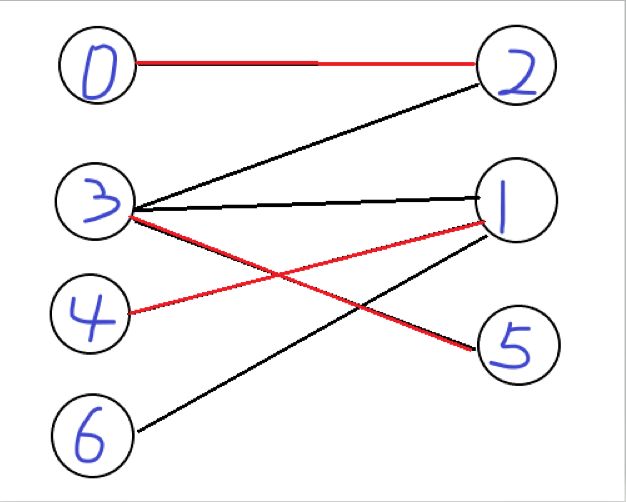
现在笔者告诉你，刚才你所完成的，就是匈牙利算法的全过程了，这张二分图的最大匹配数就是\(3\)

这里写代码的时候注意如果遇到更换的情况，新换的那个点不可以是需要让出来的那个点

对于以上繁杂的过程，笔者用了一个更加违反人类伦理的话来总结：

对于单身的小姐姐，直接去追，对于已经有男朋友的小姐姐，去问问她男朋友能不能换一个小姐姐当女朋友，把这个小姐姐让给自己

好啦不扯皮了，相信经过笔者的一通比喻，大家已经明白了匈牙利算法的实现原理了，下面来看代码吧！

这里假设我们已经对二分图染好色并存在了\(col\)数组里

bool dfs(const int x){
//match[i]存右边i号点的匹配是左边的哪个点
	for(unsigned int i=0;i

Part 4：例题

学了这么牛B（哲学）的算法，怎么能不拿出来练练手呢？

传送门：https://www.luogu.com.cn/problem/P6268

题目中给出了\(m\)条边，被边连接的两个点种只能选一个，求最多选几个点

很容易就看出来本题是求最大独立集的一道题目，由于题目中给出的只是边连接的两个点，并不知道左还是右，所以我们要先染色

染好色后（本题的数据保证是二分图了，所以不用特判）我们直接跑一遍匈牙利，然后\(n-\)最大匹配数即可

然而交上去只有\(60\)分，不知所措的我\(De\)了一下午\(bug\)，然并卵（不让下数据蛋疼），最后愤怒的我抄了个题解下来去对拍

发现：我在记录右部节点的匹配点时，默认\(match[y]==0\)是没有匹配，但是，\(TND\)这个题有个\(0\)号点，如果\(0\)号点已经和\(y\)匹配上了，查询的时候还是默认\(y\)没有匹配过，导致找到了错的增广路，然后发现匹配数比真实的答案要大\(1\)，然后\(WA\)掉了……

所以为了避免类似的惨剧发生，这里强烈建议大家把\(match\)初始化成\(-1\)，避免踩坑

\(Code\)

#include
#include
#include
#include
#include
#include
#include

好了今天关于二分图和增广路的分享就到这里了，感谢您的阅读，如果觉得笔者写的不错的话，请高抬贵手来个三连，谢谢您的支持！！！