Coursera课程自然语言处理(NLP)笔记整理(四) （第三周课程内容）

who, what, where, how, and etc

这节的基础线性代数知识太简单了，可以掠过。

1. word by word design

1.1. co-occurrence matrix

两个单词间的co-occurrence是指它们在你的语料库中在一定单词距离k内一起出现的次数

例：
比如有两句话
I like simple data
I prefer simple raw data
且k=2

	simple	raw	like	I
data	2	1	1	0

其中的2代表simple和data同时出现两次，后面两个1分别代表raw、like和data同时出现1次，0代表在k=2内I不和data同时出现

2. word by Documnet Design

例：
有Entertainment、Economy、Machine Learning三个文档

	Entertainment	Economy	Machine Learning
data	500	6620	9320
film	7000	4000	1000

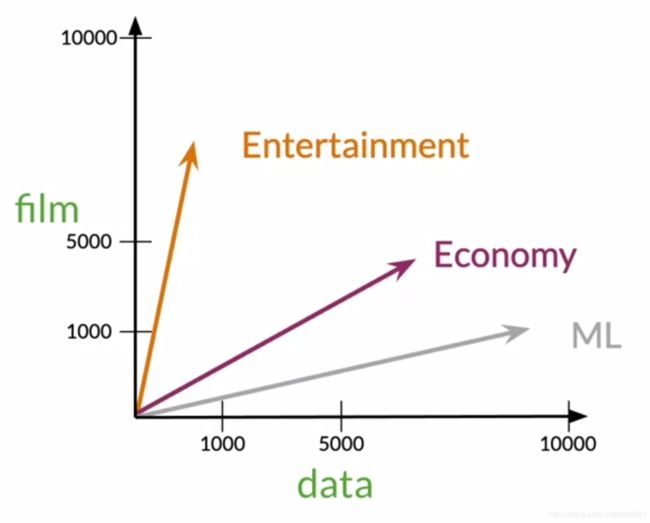< src="/pics/NLP/Vector1.png">

从图像上来讲，Economy和ML更加相近（相近:angle,distance）

3. 欧氏距离(Euclidean Distance)

在这里插入图片描述

基本数学知识，不再赘述
python 中的

v = np.array([1,6,8])
w = np.array([0,4,6])
d = np.linalg.norm(v-w)

4. 余弦相似性

图中d2 < d1，仅从距离判断，agriculture和history比agriculture和food更加接近。
另一种相似度的判断法是判断他们的余弦，角度越小则越相似。

在本例中，余弦更加适用于判断相似性。

$$v\cdot w=||v||\cdot ||w||\cos (\beta ),\cos (\beta )=\frac{v\cdot w}{||v||\cdot ||w||}$$

由于坐标都是正数，因此一定都在第一象限内，夹角一定小于90°。最相似时两向量方向相同。

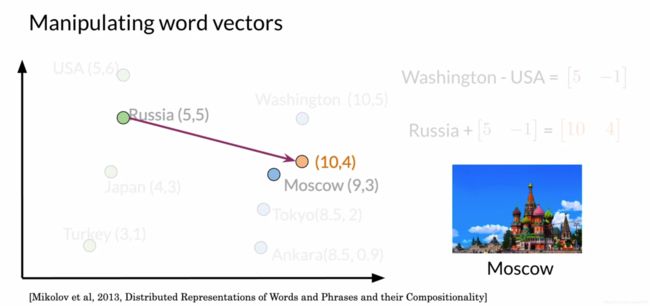
5. 向量空间与words

例：

如图所示，首先有USA到首都Washington的向量[5,-1]
借此向量来预测Russia的首都，以Russia为起点做向量，终点为[10,4]，最近的点是Moscow

6. 嵌入词的比对 Manipulating word embeddings

6.1. 引入必要的库和词库

import pandas as pd # Library for Dataframes 
import numpy as np # Library for math functions
import pickle # Python object serialization library. Not secure

word_embeddings = pickle.load( open( "word_embeddings_subset.p", "rb" ) )
len(word_embeddings) # there should be 243 words that will be used in this assignment

countryVector = word_embeddings['country'] # Get the vector representation for the word 'country'
print(type(countryVector)) # Print the type of the vector. Note it is a numpy array
print(countryVector) # Print the values of the vector.  

向量长度为300(谷歌新闻的Vocabulary size约为3 million)

#Get the vector for a given word:
def vec(w):
    return word_embeddings[w]

6.2. 嵌入词的操作

word有很多属性，我们暂且先用两个属性来堆砌进行可视化。

import matplotlib.pyplot as plt # Import matplotlib

words = ['oil', 'gas', 'happy', 'sad', 'city', 'town', 'village', 'country', 'continent', 'petroleum', 'joyful']

bag2d = np.array([vec(word) for word in words]) # Convert each word to its vector representation

fig, ax = plt.subplots(figsize = (10, 10)) # Create custom size image

col1 = 3 # Select the column for the x axis
col2 = 2 # Select the column for the y axis

# Print an arrow for each word
for word in bag2d:
    ax.arrow(0, 0, word[col1], word[col2], head_width=0.005, head_length=0.005, fc='r', ec='r', width = 1e-5)

    
ax.scatter(bag2d[:, col1], bag2d[:, col2]); # Plot a dot for each word

# Add the word label over each dot in the scatter plot
for i in range(0, len(words)):
    ax.annotate(words[i], (bag2d[i, col1], bag2d[i, col2]))


plt.show()

可得
< src ="/pics/NLP/Vector5.png">

6.3. 单词距离

words = ['sad', 'happy', 'town', 'village']

bag2d = np.array([vec(word) for word in words]) # Convert each word to its vector representation

fig, ax = plt.subplots(figsize = (10, 10)) # Create custom size image

col1 = 3 # Select the column for the x axe
col2 = 2 # Select the column for the y axe

# Print an arrow for each word
for word in bag2d:
    ax.arrow(0, 0, word[col1], word[col2], head_width=0.0005, head_length=0.0005, fc='r', ec='r', width = 1e-5)
    
# print the vector difference between village and town
village = vec('village')
town = vec('town')
diff = town - village
ax.arrow(village[col1], village[col2], diff[col1], diff[col2], fc='b', ec='b', width = 1e-5)

# print the vector difference between village and town
sad = vec('sad')
happy = vec('happy')
diff = happy - sad
ax.arrow(sad[col1], sad[col2], diff[col1], diff[col2], fc='b', ec='b', width = 1e-5)


ax.scatter(bag2d[:, col1], bag2d[:, col2]); # Plot a dot for each word

# Add the word label over each dot in the scatter plot
for i in range(0, len(words)):
    ax.annotate(words[i], (bag2d[i, col1], bag2d[i, col2]))


plt.show()

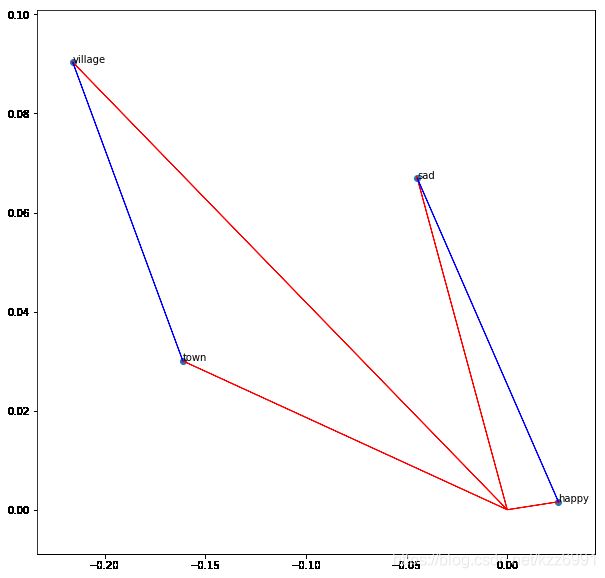< src="/pics/NLP/Vector6.png">

可以计算对应向量的范数

print(np.linalg.norm(vec('town'))) # Print the norm of the word town
print(np.linalg.norm(vec('sad'))) # Print the norm of the word sad

6.3.1. 预测首都

与前文所述方法相同
通过向量可以从Madrid向可能以Madrid为首都的国家方向移动

capital = vec('France') - vec('Paris')
country = vec('Madrid') + capital

print(country[0:5]) # Print the first 5 values of the vector

不过向量结果和spain并不相同

diff = country - vec('Spain')
print(diff[0:10])

实际上我们应当查找附近的单词，建立一个findword的方法

# Create a dataframe out of the dictionary embedding. This facilitate the algebraic operations
keys = word_embeddings.keys()
data = []
for key in keys:
    data.append(word_embeddings[key])

embedding = pd.DataFrame(data=data, index=keys)
# Define a function to find the closest word to a vector:
def find_closest_word(v, k = 1):
    # Calculate the vector difference from each word to the input vector
    diff = embedding.values - v 
    # Get the norm of each difference vector. 
    # It means the squared euclidean distance from each word to the input vector
    delta = np.sum(diff * diff, axis=1)
    # Find the index of the minimun distance in the array
    i = np.argmin(delta)
    # Return the row name for this item
    return embedding.iloc[i].name

# Print some rows of the embedding as a Dataframe
embedding.head(10)

可以找到目标国家Spain

find_closest_word(country)

'Spain'

其他国家同理

6.3.2. 将句子表达为向量

一整个句子可以表示为单词向量的求和，如

doc = "Spain petroleum city king"
vdoc = [vec(x) for x in doc.split(" ")]
doc2vec = np.sum(vdoc, axis = 0)
doc2vec

7. PCA 主成分分析

高维向量很难直观的观察，可以通过PCA将其降维成如二维向量，以便观测相似性。

7.1. 特征值和特征向量

Eignvector(特征向量) Uncorrelated features for your data 数据的不相关特征

Eignvalue(特征值) the amount of information retained by each feature 每个特性保留的信息量

7.2. 获得一组不相干特征

• 归一化数据

$$x_i=\frac{x_i-{\mu }_{x_i}}{{\sigma }_{x_i}}$$

• 获得协方差矩阵

• SVD(singular value decomposition 奇异值分解)

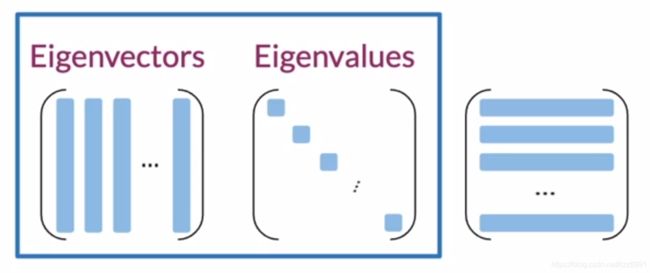< src = “/pics/NLP/Vector7.png”>

获得三个矩阵
第一个矩阵的列为特征向量，第二个矩阵的对角线元素为特征值，
第三个矩阵好可怜

• 将数据投影到新的特征组合

设特征向量矩阵为U，特征值矩阵为S

1. 将嵌入词矩阵与U进行点乘

$$X^{\prime }=XU[:,0:n]$$

n是目标维数。此处可以取2.

2. 获得新向量空间中的变量权重百分比

$$\frac{{\Sigma }_{i=0}^1{S}_{ii}}{{\Sigma }_{j=0}^d{S}_{jj}}$$

7.3. PCA的另一种解释

7.3.1. 依然是引入必要的库

import numpy as np                         # Linear algebra library
import matplotlib.pyplot as plt            # library for visualization
from sklearn.decomposition import PCA      # PCA library
import pandas as pd                        # Data frame library
import math                                # Library for math functions
import random                              # Library for pseudo random numbers

首先考虑一对随机变量x，y，若y=nx，则y和x是完全相关的。

n = 1  # The amount of the correlation
x = np.random.uniform(1,2,1000) # Generate 1000 samples from a uniform random variable
y = x.copy() * n # Make y = n * x

# PCA works better if the data is centered
x = x - np.mean(x) # Center x. Remove its mean
y = y - np.mean(y) # Center y. Remove its mean

data = pd.DataFrame({'x': x, 'y': y}) # Create a data frame with x and y
plt.scatter(data.x, data.y) # Plot the original correlated data in blue

pca = PCA(n_components=2) # Instantiate a PCA. Choose to get 2 output variables

# Create the transformation model for this data. Internally, it gets the rotation 
# matrix and the explained variance
pcaTr = pca.fit(data)

rotatedData = pcaTr.transform(data) # Transform the data base on the rotation matrix of pcaTr
# # Create a data frame with the new variables. We call these new variables PC1 and PC2
dataPCA = pd.DataFrame(data = rotatedData, columns = ['PC1', 'PC2']) 

# Plot the transformed data in orange
plt.scatter(dataPCA.PC1, dataPCA.PC2)
plt.show()

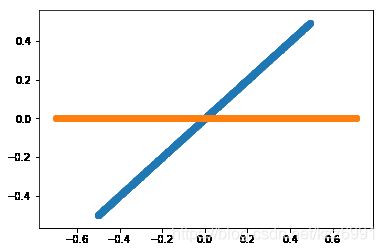< src = “/pics/NLP/Vector8.png”>

PCA结果是一条横线

7.3.2. pcaTr变换模型

7.3.2.1. 旋转矩阵

PCA模型由旋转矩阵及相关explained的方程组成。

• pcaTr.components_ 有旋转矩阵
• pcaTr.explained_variance_ 有每个主成分的 explained variance

print('Eigenvectors or principal component: First row must be in the direction of [1, n]')
print(pcaTr.components_)

print()
print('Eigenvalues or explained variance')
print(pcaTr.explained_variance_)

Eigenvectors or principal component: First row must be in the direction of [1, n]
[[-0.70710678 -0.70710678]
 [-0.70710678  0.70710678]]

Eigenvalues or explained variance
[1.59534053e-01 1.29660514e-32]

7.3.2.2. 相关正则随机变量

使用由两个具有不同方差的随机变量组成的数据集。
获得方法
创建两个独立的正太随机变量，然后用旋转矩阵将它们组合起来，新的结果变量将是原随机变量的线性组合，从而相互关联。

import matplotlib.lines as mlines
import matplotlib.transforms as mtransforms

random.seed(100)

std1 = 1     # The desired standard deviation of our first random variable
std2 = 0.333 # The desired standard deviation of our second random variable

x = np.random.normal(0, std1, 1000) # Get 1000 samples from x ~ N(0, std1)
y = np.random.normal(0, std2, 1000)  # Get 1000 samples from y ~ N(0, std2)
#y = y + np.random.normal(0,1,1000)*noiseLevel * np.sin(0.78)

# PCA works better if the data is centered
x = x - np.mean(x) # Center x 
y = y - np.mean(y) # Center y

#Define a pair of dependent variables with a desired amount of covariance
n = 1 # Magnitude of covariance. 
angle = np.arctan(1 / n) # Convert the covariance to and angle
print('angle: ',  angle * 180 / math.pi)

# Create a rotation matrix using the given angle
rotationMatrix = np.array([[np.cos(angle), np.sin(angle)],
                 [-np.sin(angle), np.cos(angle)]])


print('rotationMatrix')
print(rotationMatrix)

xy = np.concatenate(([x] , [y]), axis=0).T # Create a matrix with columns x and y

# Transform the data using the rotation matrix. It correlates the two variables
data = np.dot(xy, rotationMatrix) # Return a nD array

# Print the rotated data
plt.scatter(data[:,0], data[:,1])
plt.show()

angle:  45.0
rotationMatrix
[[ 0.70710678  0.70710678]
 [-0.70710678  0.70710678]]

将原始数据也画出来

plt.scatter(data[:,0], data[:,1]) # Print the original data in blue

# Apply PCA. In theory, the Eigenvector matrix must be the 
# inverse of the original rotationMatrix. 
pca = PCA(n_components=2)  # Instantiate a PCA. Choose to get 2 output variables

# Create the transformation model for this data. Internally it gets the rotation 
# matrix and the explained variance
pcaTr = pca.fit(data)

# Create an array with the transformed data
dataPCA = pcaTr.transform(data)

print('Eigenvectors or principal component: First row must be in the direction of [1, n]')
print(pcaTr.components_)

print()
print('Eigenvalues or explained variance')
print(pcaTr.explained_variance_)

# Print the rotated data
plt.scatter(dataPCA[:,0], dataPCA[:,1])

# Plot the first component axe. Use the explained variance to scale the vector
plt.plot([0, rotationMatrix[0][0] * std1 * 3], [0, rotationMatrix[0][1] * std1 * 3], 'k-', color='red')
# Plot the second component axe. Use the explained variance to scale the vector
plt.plot([0, rotationMatrix[1][0] * std2 * 3], [0, rotationMatrix[1][1] * std2 * 3], 'k-', color='green')

plt.show()

Eigenvectors or principal component: First row must be in the direction of [1, n]
[[-0.70825968 -0.705952  ]
 [ 0.705952   -0.70825968]]

Eigenvalues or explained variance
[1.02258823 0.11290988]

< src="/pics/NLP/Vector9.png">

其意义为：用PCA变换找出用于创建相关变量(蓝色)的旋转矩阵，使用PCA模型变换我们的数据，将这些变量作为我们的原始不相干变量。

8. 附：最简单的Numpy与线性代数

8.1. numpy array 与 list的区别

• 数据类型

import numpy as np  # The swiss knife of the data scientist.
alist = [1, 2, 3, 4, 5]   # Define a python list. It looks like an np array
narray = np.array([1, 2, 3, 4]) # Define a numpy array
print(alist)
print(narray)

print(type(alist))
print(type(narray))

结果为

[1, 2, 3, 4, 5]
[1 2 3 4]
<class 'list'>
<class 'numpy.ndarray'>

8.2. 运算

8.2.1. 加法

print(narray + narray)
print(alist + alist)

[2 4 6 8]
[1, 2, 3, 4, 5, 1, 2, 3, 4, 5]

8.2.2. 乘法

print(narray * 3)
print(alist * 3)

[ 3  6  9 12]
[1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5]

8.3. 矩阵

npmatrix1 = np.array([narray, narray, narray]) # Matrix initialized with NumPy arrays
npmatrix2 = np.array([alist, alist, alist]) # Matrix initialized with lists
npmatrix3 = np.array([narray, [1, 1, 1, 1], narray]) # Matrix initialized with both types

print(npmatrix1)
print(npmatrix2)
print(npmatrix3)

矩阵每行应有相同数量的元素，不然可能出现非预期结果

badmatrix = np.array([[1, 2], [3, 4], [5, 6, 7]]) # Define a matrix. Note the third row contains 3 elements
print(badmatrix) # Print the malformed matrix
print(badmatrix * 2) # It is supposed to scale the whole matrix
[list([1, 2]) list([3, 4]) list([5, 6, 7])]
[list([1, 2, 1, 2]) list([3, 4, 3, 4]) list([5, 6, 7, 5, 6, 7])]

8.3.1. 矩阵的运算

okmatrix = np.array([[1, 2], [3, 4]])
# Scale by 2 and translate 1 unit the matrix
result = okmatrix * 2 + 1 # For each element in the matrix, multiply by 2 and add 1
print(result)
[[3 5]
 [7 9]]
# Add two sum compatible matrices
result1 = okmatrix + okmatrix
print(result1)

# Subtract two sum compatible matrices. This is called the difference vector
result2 = okmatrix - okmatrix
print(result2)
[[2 4]
 [6 8]]
[[0 0]
 [0 0]]

乘法默认是元素相乘

result = okmatrix * okmatrix # Multiply each element by itself
print(result)
[[ 1  4]
 [ 9 16]]

8.3.2. 矩阵的转置

matrix3x2 = np.array([[1, 2], [3, 4], [5, 6]]) # Define a 3x2 matrix
print('Original matrix 3 x 2')
print(matrix3x2)
print('Transposed matrix 2 x 3')
print(matrix3x2.T)
Original matrix 3 x 2
[[1 2]
 [3 4]
 [5 6]]
Transposed matrix 2 x 3
[[1 3 5]
 [2 4 6]]

但是这对1D array无效

nparray = np.array([1, 2, 3, 4]) # Define an array
print('Original array')
print(nparray)
print('Transposed array')
print(nparray.T)
Original array
[1 2 3 4]
Transposed array
[1 2 3 4]

除非操作改为

nparray = np.array([[1, 2, 3, 4]]) # Define a 1 x 4 matrix. Note the 2 level of square brackets
print('Original array')
print(nparray)
print('Transposed array')
print(nparray.T)

Original array
[[1 2 3 4]]
Transposed array
[[1]
 [2]
 [3]
 [4]]

8.3.3. 矩阵的范数

2范数的定义为

$$norm(a)=||a||=\sqrt{{\Sigma }_{i=1}^n{a}_I^2}$$

如果无axis参数则计算矩阵的范数

nparray1 = np.array([1, 2, 3, 4]) # Define an array
norm1 = np.linalg.norm(nparray1)

nparray2 = np.array([[1, 2], [3, 4]]) # Define a 2 x 2 matrix. Note the 2 level of square brackets
norm2 = np.linalg.norm(nparray2) 

print(norm1)
print(norm2)

如果有参数axis
axis=0 为行
axis=1 为列

nparray2 = np.array([[1, 1], [2, 2], [3, 3]]) # Define a 3 x 2 matrix. 

normByCols = np.linalg.norm(nparray2, axis=0) # Get the norm for each column. Returns 2 elements
normByRows = np.linalg.norm(nparray2, axis=1) # get the norm for each row. Returns 3 elements

print(normByCols)
print(normByRows)

[3.74165739 3.74165739]
[1.41421356 2.82842712 4.24264069]

8.3.4. 点乘

定义为

$$a\cdot b={\Sigma }_{i=1}^n{a}_i{b}_i$$

nparray1 = np.array([0, 1, 2, 3]) # Define an array
nparray2 = np.array([4, 5, 6, 7]) # Define an array

flavor1 = np.dot(nparray1, nparray2) # Recommended way
print(flavor1)

flavor2 = np.sum(nparray1 * nparray2) # Ok way
print(flavor2)

flavor3 = nparray1 @ nparray2         # Geeks way
print(flavor3)

# As you never should do:             # Noobs way
flavor4 = 0
for a, b in zip(nparray1, nparray2):
    flavor4 += a * b
    
print(flavor4)

8.3.5. 按行或列求和

axis=0 为行
axis=1 为列

nparray2 = np.array([[1, -1], [2, -2], [3, -3]]) # Define a 3 x 2 matrix. 

sumByCols = np.sum(nparray2, axis=0) # Get the sum for each column. Returns 2 elements
sumByRows = np.sum(nparray2, axis=1) # get the sum for each row. Returns 3 elements

print('Sum by columns: ')
print(sumByCols)
print('Sum by rows:')
print(sumByRows)

8.3.6. 按行或列求平均

axis=0 为行
axis=1 为列

nparray2 = np.array([[1, -1], [2, -2], [3, -3]]) # Define a 3 x 2 matrix. Chosen to be a matrix with 0 mean

mean = np.mean(nparray2) # Get the mean for the whole matrix
meanByCols = np.mean(nparray2, axis=0) # Get the mean for each column. Returns 2 elements
meanByRows = np.mean(nparray2, axis=1) # get the mean for each row. Returns 3 elements

print('Matrix mean: ')
print(mean)
print('Mean by columns: ')
print(meanByCols)
print('Mean by rows:')
print(meanByRows)

8.3.7. 按行中心化矩阵

nparray2 = np.array([[1, 1], [2, 2], [3, 3]]) # Define a 3 x 2 matrix. 

nparrayCentered = nparray2 - np.mean(nparray2, axis=0) # Remove the mean for each column

print('Original matrix')
print(nparray2)
print('Centered by columns matrix')
print(nparrayCentered)

print('New mean by column')
print(nparrayCentered.mean(axis=0))

Original matrix
[[1 1]
 [2 2]
 [3 3]]
Centered by columns matrix
[[-1. -1.]
 [ 0.  0.]
 [ 1.  1.]]
New mean by column
[0. 0.]