《Cascade R-CNN: Delving into High Quality Object Detection》论文笔记

传送门：

1. Cascade R-CNN训练自己的数据
2. Cascade R-CNN Python测试脚本

1. 概述

在目标检测任务中通常使用IOU阈值来区分正负例，在检测任务中将阈值设置为0.5会带来检测噪声。但是检测的性能表现会随着IOU阈值的增加而变差，其主要源自于两个原因：

• 1）提高网络的IOU阈值，会导致训练时由于正样本指数消失，从而导致网络过拟合；
• 2）detector肯定是在某一个IOU阈值上训练的，但是inference时，生成anchor box之后，这些anchor box跟ground truth box会有各种各样的IOU，对于这些IOU来说detector是次优化的；

论文提出了Cascade R-CNN多阶段目标检测框架来解决这个问题，它由一系列不同IOU阈值的检测器组成，以便对接近假阳性检测框的有更多的选择。整个网络是逐阶段训练的，当前阶段的网络为下一个阶段网络训练提供更好的分布。逐步改进的假设的重采样保证了所有探测器都有一组等效尺寸的正的例子，从而减少了过拟合问题。同样的级联程序应用于推理，使假设与每个阶段的检测器质量之间能够更紧密地匹配。Cascade R-CNN模型已经超越了当今在COCO数据集的单模型检测器。实验表明Cascade R-CNN在多个检测网络结构上运用， 都超过了原有的base。代码地址：cascade-rcnn

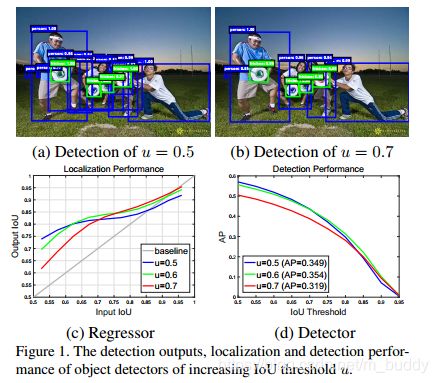
在上面的（a）图中使用的IOU阈值是0.5，产生了很多假阳性的检测区域；当把阈值设置为0.7的时候图中假阳性区域明显减少，检测的结果更准确，如上图（b）所示；图（c）展示的定位的性能，其中的横坐标是输入proposal的IOU，纵坐标输出是检测结果的IOU，从横向看开始时小一些的IOU阈值会表现的好一些，到后期是IOU阈值大的表现更好，但是这样会出现正样本减少，网络过拟合的问题；图（d）是检测的性能，上面展示不同的IOU阈值对于最后AP的影响，先是0.5在上面后面是0.6，这说明不同质量的proposals最好对应不同能力的检测分支来操作，如果想得到高质量的检测结果，更需要在不同IOU阈值下训练的检测分支调整能力，与对应的hypotheses质量更匹配，这也是作者要提出多阶段不同IOU阈值检测的原因；

2. 目标检测

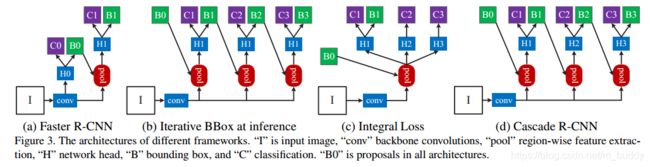
(a)就是经典的Faster R-CNN框架，也是本文的baseline；（b）结构上和Cascade R-CNN非常相似，区别在于只在测试时采用级联结构对Box多次回归，因此ROI检测网络部分“H1”结构是相同的，也即训练时还是采用的单一的IoU阈值；（c）则是在ROI检测网络部分并联多个检测器，这些检测器是不相关的。
在这一节中主要分析上图（b）和（c）两种改进结构中存在的问题，在下一节中讲论文提出的新的网络结构。

2.1 边界框回归

对于边界框$b=(b_x,b_y,b_w,b_h)$，边界回归是将候选边界框$b$回归到目标边界框$g$，使用的回归函数是$f(x,b)$。网络从样本$\{g_i,b_i\}$计算残差进行学习，损失函数可以描述为：

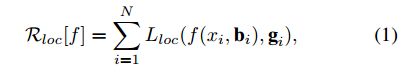
对于$L_{loc}$在R-CNN中使用的是L_2范数，在Faster R-CNN中使用的是L_1范数。$L_{loc}$去回归边界框坐标的差值$({\delta }_x,{\delta }_y,{\delta }_w,{\delta }_h)$，这四个差值被描述为：

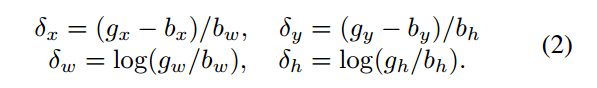
一般来说这里差值是很小的，为了提升多任务训练的效率文章中对其进行了归一化，对于${\delta }_x$使用${\delta }_x^{{}^{\prime }}=({\delta }_x-{\mu }_x)/{\sigma }_x$进行替换。

2.2 改进方法1

论文中提到$f$的一个回归步骤不足以精确定位。相反，$f$被迭代地应用，作为后处理步骤来改善边界框$b$。

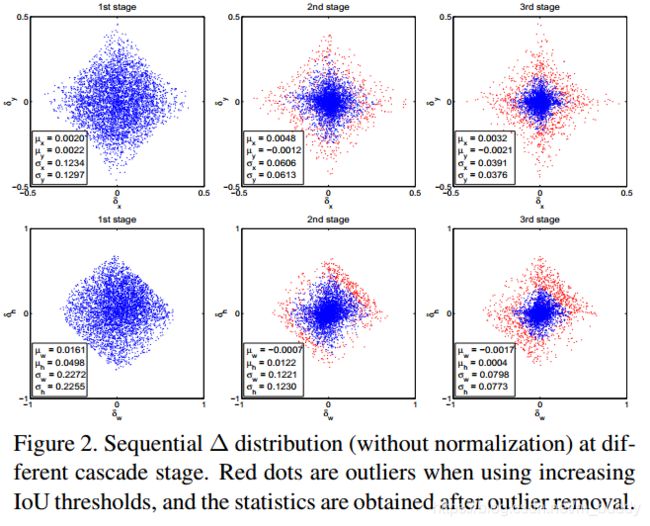
上图是边界框的残差分布，增大IOU的阈值，红点是异常值，去除异常值后得到统计量。

上述形式为迭代边界框回归，表示为迭代BBOX。它可以用图3(b)的推断架构来实现，其中所有的头部都是相同的。然而，这种想法忽略了两个问题。首先，如图1所示，在u=0.5处训练的回归系数$f$对于较高的IOU假设是次优的。其次，如图2所示，在每次迭代之后，边界框的分布都会发生显着变化。虽然回归量对于初始分布是最优的，但在此之后，它可能是相当次优的。由于这些问题，迭代BBOX需要大量的人工干预设置参数，因而通常使用超过两次$f$没有任何好处。
其实就是说按照图3（b）中的结构使用相同的IOU阈值进行边界框检测会存在边界框分布的问题，需要人工去设置很多东西。
存在的问题：

• 1）三个head部分是一样的，也就是说都是针对某一个IOU阈值，比如0.5，是最优化的，但是当inference时，真正的IOU大于0.5以后他是次优化suboptimal 的。
• 2）很明显级联之后，每个输出的box的分布是会变化的如上图 Figure (2)，所以相同的head对于后面的结构来说是次优化的suboptimal 。

2.3 改进方法2

目标分类使用函数$h(x)$将预测框分类到$M+1$类别中去，其中0是背景类。对于分类的损失函数定义如下，是一个典型的交叉熵损失函数：

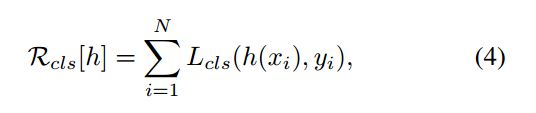
对于RPN网络输出的结果好坏判定是通过一个阈值$u$实现的，大于该阈值的被判定为正例，相反便是负例。

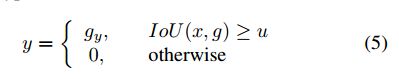
如果将阈值设置的比较高，那么正样本会很少，这样网络会过拟合；若是过低会带来较多的假阳性检测区域。针对这样有人将IOU集成到分类的损失中去，得到如下的损失函数：

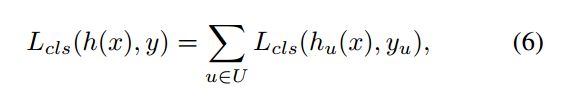
其中，$U\in \{0.5,0.55,\dots ,0.75\}$，该网络的结构如图3（c）所示。在下图第一幅图中，IOU阈值高，正样本就很少，会带来过拟合。

上图中是三个阶段中训练样本IOU的分布，每个图中红色的文字代表大于对应IOU所占的比例。最后证明该改进的效果并不是很理想。

3. Cascade R-CNN

本文中提出的网络结构是如图3（d）图所示的结构。

3.1 Cascade边界框回归

图3（d）中的级联回归可以被描述为：

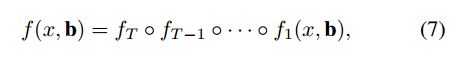
其中$b=f_{t-1}(x^{t-1},b^{t-1})$，它在几个方面不同于图3(b)的迭代BBOX体系结构:

• 1）迭代BBOX是用于改进边界框的后处理过程，而级联回归是一种重采样过程，它改变了不同阶段要处理的假设的分布
• 2）由于它既用于训练又用于推理，因此训练和推理分布之间没有差异。
• 3）针对不同阶段的重采样分布，对多个特殊回归器$\{f_T,f_{T-1},\dots ,f_1\}进行了优化。这与图3（b）的单个$f$相反，后者仅对初始分布是最优的。与迭代BBOX相比，这些差异使定位更加精确，没有人工干预。

$({\delta }_x,{\delta }_y,{\delta }_w,{\delta }_h)$在之前的内容中需要通过其均值和方差进行归一化，才能有效地进行多任务学习。在每个回归阶段之后，这些统计数据将按顺序演变，如图2所示。在训练时，相应的统计信息将用于在每个阶段规范残差。

3.2 级联检测

如图4左图所示，最初假设(如RPN proposal)的分布严重倾向于低质量。这不可避免地导致了对高质量分类器的无效学习。Cascade R-CNN依靠级联回归作为重采样机制来解决这个问题。这是因为在图1（c）中，所有曲线都在对角灰色线之上，即为某个确切u值训练的边界框回归器倾向于产生较高的IOU边界框。因此，从一组示例$(x_i,b_i)$开始，级联回归成功重采样出一个有高IoU的分布$(x_i^{{}^{\prime }},b_i^{{}^{\prime }})$ 。这样，即使提高了探测器质量(IOU阈值)，也有可能使连续各阶段的一组正例保持在大致恒定的大小。这在图4中（后面的两个阶段IOU的分布）得到了说明，在每个重采样步骤之后，分布更倾向于高质量的示例。随后产生了两个后果。首先，没有存在过拟合的情况，因为在所有级别上都有大量的例子。其次，针对较高的IOU阈值，对较深阶段的检测器进行了优化。请注意，一些异常值是通过增加IOU阈值来依次删除的，如图2所示，从而实现了经过更好训练的专用检测器序列。
在每个阶段t，R-CNN包括一个分类器$h_t$和一个针对IOU阈值$u_t$优化的回归器$f_t$，其中$u_t>u_{t-1}$，这是通过最小化下面的损失函数来保证。

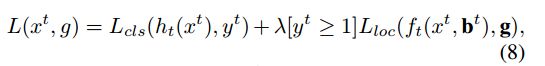
4. 实验

Cascade R-CNN有四个阶段，一个RPN和三个检测$U=\{0.5，0.6，0.7\}$的三个阶段。在RPN之后，重采样是通过简单地使用前一阶段的回归输出来实现的。

4.1 检测的质量需要与之匹配的RPN输入

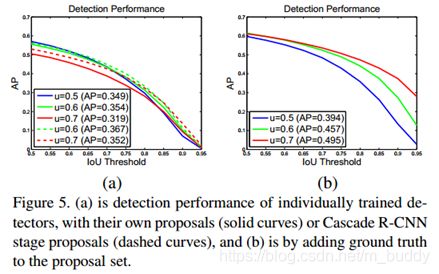
在图5（a）图中的开始阶段u=0.5是较好的AP曲线，但是随着横轴往右，u=0.7成为了最好的曲线。在图（b）中使用ground truth作为RPN的输出，可以看出u=0.7的效果是高于所有的u值的。这张图说明了两点：

• 1）u=0.5并不是对高精度检测的最佳阈值，仅仅只是对较低质量的RPN结果具有较好的鲁棒性；
• 2）高精度的检测需要与之匹配的输入分布，也就是你要想好那么对应的输入也是应该好的。

同理，在Cascade R-CNN的三个阶段（三个阶段阈值分别为：$0.5,0.6,0.7$）中也可以看出，什么样的输入就应该跟什么样的阈值进行匹配，如下图所示：

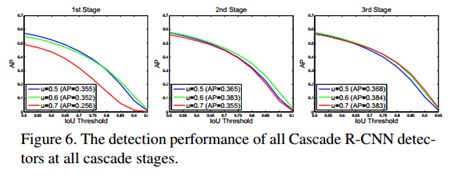
三条曲线分别标明了三个阶段最适宜的IOU阈值，输入质量越好那么对应的阈值越高。

4.2 与现今方法的比较

作者选用了三种two-stage的检测器：Faster R-CNN、R-FCN和FPN，从下表中可以发现：在不加任何trick的情况下，对于不同的检测器和不同的基准网络，采用层叠的方式提高IOU阈值来提纯样本，Cascade均能稳定提升3-4个点左右：

此外，论文给出了大量的剥离实验来验证Cascade的有效性见下图中的四张表：

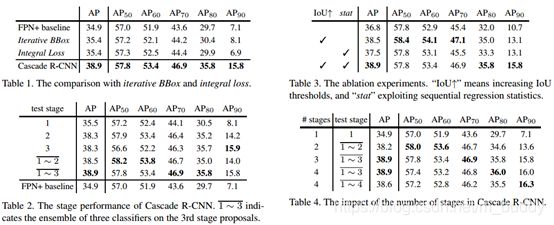
从中上面的表数据可以得出以下结论：

• 1） 表1充分展示了Cascade较Iterative BBox和Intergral loss的优越性，尤其是在$A{P}_{90}$ 。评估指标上，说明提高IoU阈值训练级联检测器的必要性；
• 2） 表2展示了联合多个分类器的分类得分的必要性，在AP指标上，stage2比stage1展现了3个点的性能提升，而stage3并没有比stage2展现优势，而联合多个分类器的分类得分可以将AP提升到38.9；
• 3） 表3展示了提高IoU阈值以及利用不同回归统计信息的必要性，第二行与第四行的对比表明前者比后者更为重要，再次证明提高IoU阈值训练级联检测器的必要性；
• 4） 表4展示了采用几个stage会使性能达到饱和，可以发现stage4已经无法带来性能提升，stage3可以达到AP的最高点38.9，而stage2带来的性能提升最为明显，因此对于实际应用而言，两个stage已经足够。

5. REF

1. 目标检测-Cascade R-CNN-论文笔记
2. CVPR 2018|Cascade R-CNN：向高精度目标检测器迈进