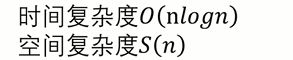八大排序
目录
1、冒泡排序
2、插入排序
3、选择排序
4、计数排序--桶排序
5、归并排序
6、堆排序
7、快速排序 -----单路
8、快速排序 -----双路
9、快速排序 ----三路
1、冒泡排序
定义指针j,如果默认为从小到大的顺序进行排序,j和j+1比较,如果j>j+1,则交换两个元素的位置即可,依次循环。(相当于每一轮比较完找到的是最大值)
public class BubbleSort {
public static void bubbleSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
}
}
}
}
private static void swap(int[] arr, int j, int i) {
// TODO Auto-generated method stub
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}2、插入排序
定义两个指针i、j均指向角标1处,j-1指向j的前一个元素,当j-1>=0的时候(也就是有元素的时候),比较j和j-1的大小,如果j>j-1,则交换所指向的两个元素交换位置,j和j-1前移,知道j-1<0,i++,然后j指向i所指向的元素,再次比较j和j-1元素的值,依次循环,直至遍历完整个数组。
public class InsertSort {
public static void insertSort(int[] arr){
int e;
int j;
for(int i=1;i0&&arr[j-1]>e;j--) {
arr[j]=arr[j-1];
}
arr[j]=e;
}
}
/*private static void swap(int[] arr, int j, int i) {
// TODO Auto-generated method stub
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}*/
public static void insertSort(int[] arr,int l,int r){
int e;
int j;
for(int i=l+1;i0&&arr[j-1]>e;j--) {
arr[j]=arr[j-1];
}
arr[j]=e;
}
}
} 3、选择排序
当前值(角标0)和后面的每一个元素逐一进行比较,如果前者大于后者,交换位置,然后角标1出的元素和后面依次比较,原理相同,知道最后一个元素。(相当于每一轮比较找到的是最小值)
public class SelectSort {
public static void selectSort(int[] arr){
for(int i=0;iarr[j]) {
swap(arr,i,j);
}
}
}
}
private static void swap(int[] arr, int j, int i) {
// TODO Auto-generated method stub
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
} 4、计数排序--桶排序
public class CountSort {
public static void countSort(int[] arr) {
int max = findMax(arr);
int min = findMin(arr);
int len = max - min + 1;
int[] counts = new int[len];
int offset = 0 - min;
for (int i = 0; i < arr.length; i++) {
counts[arr[i] + offset]++;
}
int index = 0;
for (int i = 0; i < counts.length;) {
while (counts[i] != 0) {
arr[index++] = i -offset;
counts[i]--;
}
}
}
private static int findMin(int[] arr) {
int min = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] < min) {
min = arr[i];
}
}
return min;
}
private static int findMax(int[] arr) {
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
return max;
}
}
5、归并排序
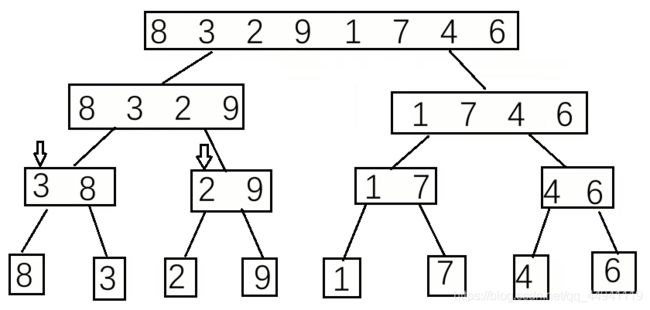
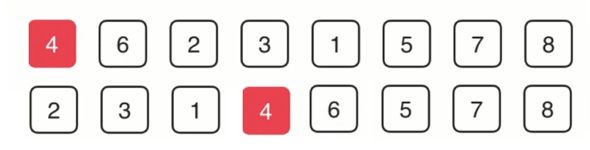
将数组想象也就是相当于一个二叉树,讲其一分为二,如下图:
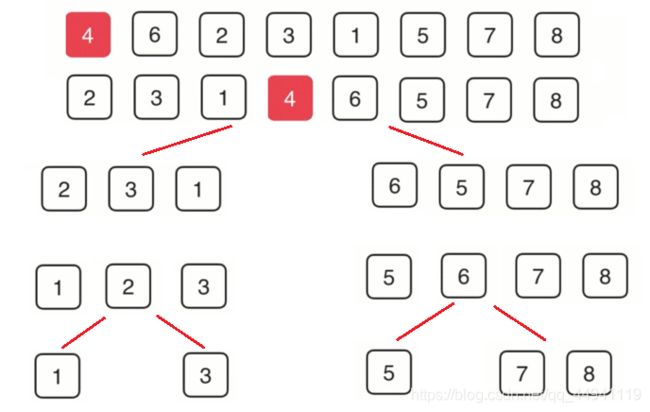
根据一分为二的思想(直到不能分为止)可以分成如下图:
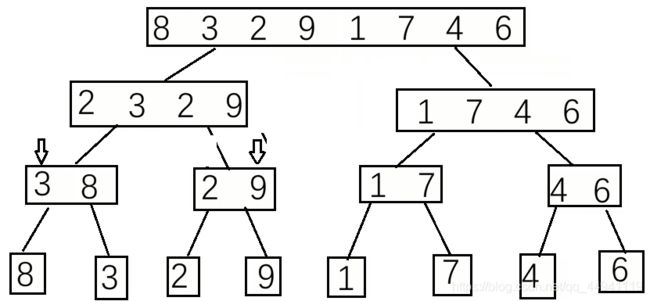
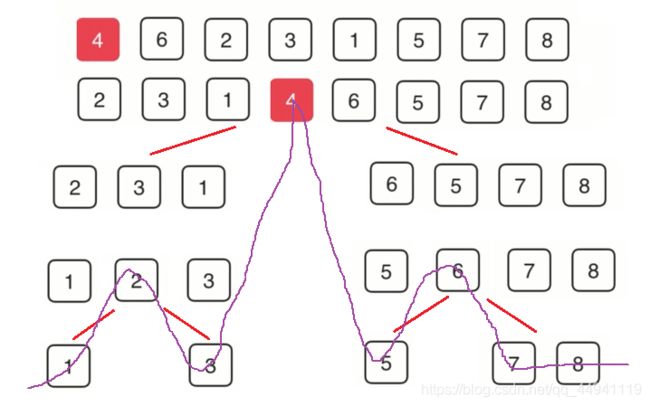
分完之后,就是回溯的方法,比如8和3是从数组[8,3]二分来的,然后用回溯的思想给3和8进行排序,3<8,所以3先进入他俩的父节点(数组),最后一层回溯完的结果如图:
接下来继续回溯,[3,8] [2,9]里面肯定要先找到最小的值先回溯给它们的父节点,所以这时候就需要两个指针,一个指向[3,8]中的3,一个指向[2,9]中的2,比较两个指针的值的大小,小的先回溯,指向小的指针后移,指向大值的指针不动,然后继续比较大小,如图:
然后依次循环。
public class MergeSort {
public static void mergeSort(int[] arr){
mergeSort(arr,0,arr.length-1);
}
private static void mergeSort(int[] arr, int l, int r) {
// TODO Auto-generated method stub
//优化2
/*if(l>=r) {
return;
}*/
if(r-l<=15) {
InsertSort.insertSort(arr,r,l);
}
int mid=(l+r)/2;
mergeSort(arr,l,mid);
mergeSort(arr,mid+1,r);
//优化1
if(arr[mid]>arr[mid+1]){
merge(arr,l,mid,r);
}
}
private static void merge(int[] arr, int l, int mid, int r) {
// TODO Auto-generated method stub
int[] aux=new int[r-l+1];
for(int i=l;i<=r;i++) {
aux[i-l]=arr[i];
}
int i=l;
int j=mid+1;
for(int k=l;k<=r;k++) {
if(i>mid) { //左边走完
arr[k]=aux[j-l];
j++;
}else if(j>r) { //右边走完
arr[k]=aux[i-l];
i++;
}else if(aux[i-l]<=aux[j-l]){
arr[k]=aux[i-l];
i++;
}else{
arr[k]=aux[j-l];
j++;
}
}
}
}
6、堆排序
堆排序是基于最大堆的实现,所谓最大堆就是其左右子树都不大于根,并没有规定是否左小右大,在这里我们采用下沉的方法,如下图我们现在访问的是6,那么我们只要选择 这个子树,将3下沉,从而转变为
这个子树,将3下沉,从而转变为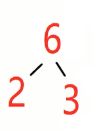 。依次循环
。依次循环
public class HeapSort {
public static void heapSort(int[] arr) {
Integer [] nums=new Integer[arr.length];
for(int i=0;i heap=new MaxHeap(nums);
int index=arr.length-1;
while(!heap.isEmpty()) {
arr[index--]=heap.extractMax();
}
}
}
7、快速排序 -----单路
快速排序就是默认第一个数为中间数,将数组分为两个部分,但是有极端问题也就是快排的问题就是可能第一个数字的右边都比它大或者都比它小,这就是快速排序的一个缺点。
以第一个数字为中间数分成两个部分,如图:
然后一致按照这个原理进行分割,直到不能分为止,如图:
排序完的结果就是1 2 3 4 5 6 7 8
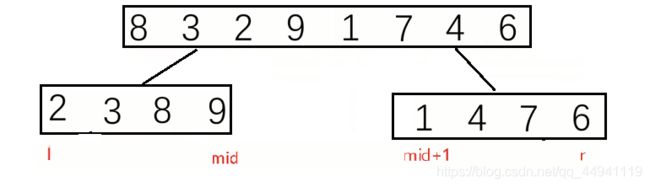
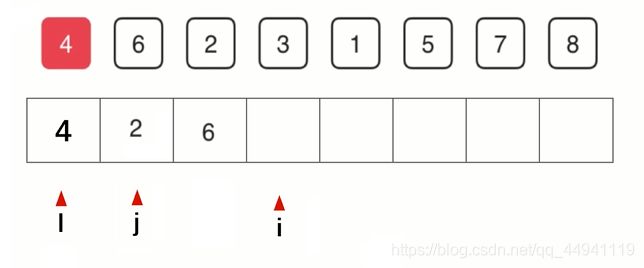
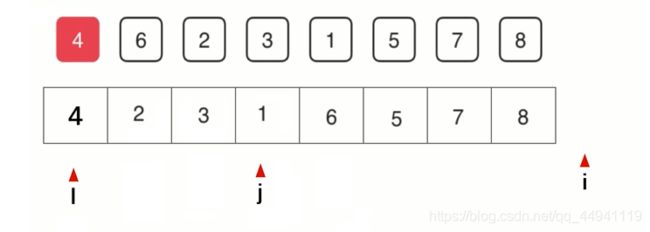
所以我们需要定义指针i,j,l,l和j从最左边开始,i从l+1开始,l就是中间值所以l不动
然后依次比较,6>4,所以6到i所指向的位置,i后移,2<4,2和j+1的位置互换,j后移,i后移,依次类推。
等上述操作完成之后,l和j交换位置
public class QuickSort1 {
public static void quickSort(int[] arr) {
quickSort(arr,0,arr.length-1);
}
private static void quickSort(int[] arr, int l, int r) {
// TODO Auto-generated method stub
/*if(l>=r) {
return;
}*/
if(r-l<=15) {
InsertSort.insertSort(arr,l,r);
}
int p=partition(arr,l,r);
quickSort(arr,l,p-1);
quickSort(arr,+1,r);
}
//返回P
private static int partition(int[] arr, int l, int r) {
swap(arr,l,(int)(Math.random()*(r-l+1)+l));
int v=arr[l];
int j=l;
for(int i=l+1;i8、快速排序 -----双路
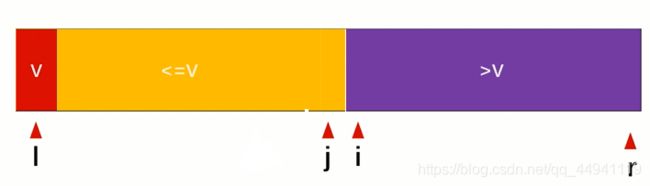
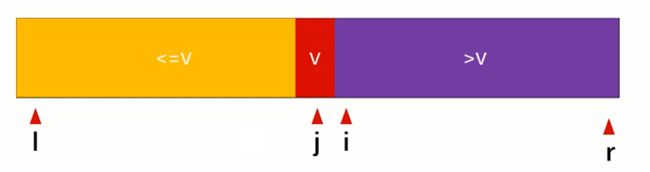
i指向小于中间值(默认第一个数字就是中间值)的后一个数(i-1是小于中间值的最后一个),如果接下来的值小于v,黄色的部分增加一个,i后移,如果大于v,紫色部分扩,j前移,始终是先移动i,后移动j,当i>j时候结束循环,j和l换位置即可。
public class QuickSort2 {
public static void quickSort(int[] arr) {
quickSort(arr,0,arr.length-1);
}
private static void quickSort(int[] arr, int l, int r) {
// TODO Auto-generated method stub
if(r-l<=15) {
InsertSort.insertSort(arr,l,r);
}
int p=partition(arr,l,r);
quickSort(arr,l,p-1);
quickSort(arr,+1,r);
}
private static int partition(int[] arr, int l, int r) {
// TODO Auto-generated method stub
swap(arr,l,(int)(Math.random()*(r-l+1)+l));
int v=arr[l];
int i=l+1;
int j=r;
while(true) {
while(i<=r&&arr[i]=l+1&&arr[j]>v) {
j--;
}
if(i>j) {
break;
}
swap(arr,i,j);
i++;
j--;
}
swap(arr,l,j);
return j;
}
private static void swap(int[] arr, int j, int i) {
// TODO Auto-generated method stub
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
9、快速排序 ----三路
首先我们要明白三路排是二路排的一种优化,图中的i指的是某一个元素e,如果元素e小于v,lt+1和i互换,i后移,lt后移,如果e大于v,gt-1和i互换,gt前移。直到i等于gt的时候表示循环结束,最后l和lt交换位置。
public class QuickSort3 {
public static void quickSort(int[] arr) {
quickSort(arr,0,arr.length-1);
}
private static void quickSort(int[] arr, int l, int r) {
// TODO Auto-generated method stub
if(r-l<=15) {
InsertSort.insertSort(arr,l,r);
return;
}
swap(arr,l,(int)(Math.random()*(r-l+1)+l));
int v=arr[l];
int lt=l;
int gt=r+1;
int i=l+1;
while(i