常用数据结构与算法:union find(并查集)
一:union find简介
二:union find实现
三:union find应用举例
一:union find简介
union find 并查集是专门针对检测动态连通性的一种数据结构。什么问题会用到动态连通性?举个简单的例子当我们有一张图,上面连满了点如何判断两个点之间是否有可以连通的路径。
并集查通常用来解决图的连通性的问题。“图”当然不仅仅限于图片。图片中的两个像素点是否连通可以用union find,人与人直接的关系此类联系也通常可以看作是图,比如我们想查看在N个人的朋友关系中,其中的两个人是否有间接的联系我们也可以用union find。
union的运用集中在解决是否具有连通性此类问题上,当如下事物需要解决一些联通性问题时运用union find这种数据结构来模拟非常合适:
- 图片中的像素点Tarjan算法
- 计算机网络中的节点
- 社交网络中的节点
- 数学集合中的元素
union find算法的一些经典应用包括:
- Hoshen-Kopelman算法 (用来判断网格中节点的连续性)
- Kruskal最小生成树算法
- Tarjan算法 (寻找最近公共祖先)
- Prelocation theory (物理,化学中的著名理论,不太了解)
二:union find的实现
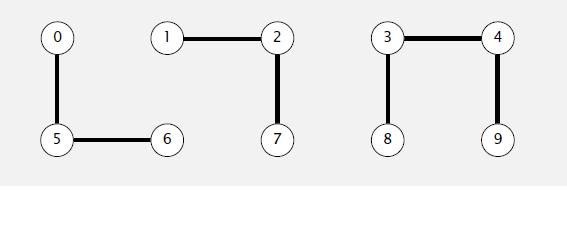
| 0 | 1 | 1 | 3 | 3 | 0 | 1 | 3 | 3 |
在这之中 0,5,6都是联通的,所以他们的根节点应该为一样0。1,2,7联通对应的元素根节点都为1。3,4,8,9联通对应的根节点3。(为了简单我们暂时将所有节点的值都设为他们的根节点)
查找操作:
查找两个节点是否连通,我们可以通过两个节点的根节点是否相同来进行比较。查找一个节点根节点的操作就是递归查找该节点父节点的操作。
int root(int i)
{
while(i!=_array[i]) //根元素条件_array[i]=i
i=_array[i];
return i;
}bool is_connected(int i ,int j )
{
return true:false ? root(i) == root(j);
}合并操作:
合并两个节点的操作,一种非常简便的操作即是让其中一个节点的根节点的值变为另外一个节点根节点的值。即是削掉一个根节点让它的父节点等于另外一个节点的根节点。
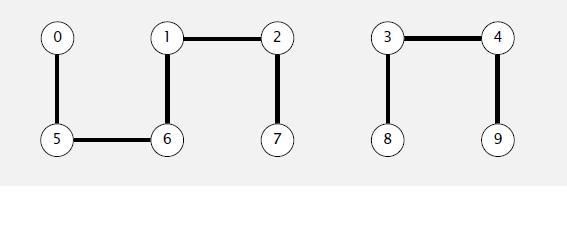
我们还是以上面的图为例子,假设我们现在合并节点1和6(我们总是让后一个节点的根节点改变),我们只要让6的根节点的父节点变为1的根节点就行了
| 0 | 0 | 1 | 3 | 3 | 0 | 1 | 3 | 3 |
这里我们将array[1]的父节点改为了0,因为array[1]是1,2,7集合的根节点,而0是0,5,6集合的根节点。
void union(int i , int j ) //联通节点i,j
{
_array[root(j)] = root(i); //将j的根节点的父节点设为i的根节点
}用这种方式实现的并查集叫做快速并查集(quick-union)。quick-union的合并操作最坏操作时间O(n),最坏查找连通性时间O(n)。如果按照平均来说应该是介于O(lgn)与O(n)之间。
改进一 平衡并查集:
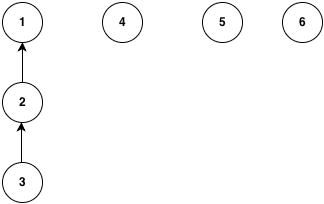
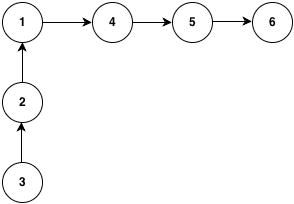
上面只是一个最基本的并集查找的实现,这个实现有一个非常知名的缺陷就是在某种特殊情况下它的查找和合并操作的耗时接近O(n)。为什么会出现这种最坏的情况?看下面的图
当我们执行操作union(4,1),union(5,1),union(6,1)时,因为我们总是改变1的根节点指向前一个节点所以造成下面这种情况。
当我们查找3的根节点的时候我们将耗时6步,即O(n)。
改变这种情况的方法就是当我们执行union操作的时候先判断联通的两个节点的哪边的集合大,我们把小的节点连接到大的节点的根节点就可以避免这种情况了。(刚才造成上面极端情况的原因的我们老是把大的集合的根节点连接到小的集合的根节点)。这种改进便是所说的平衡并查集(weighted quick-union)。
平衡并查集的实现需要除了原有的存储数据,还要加上各个集合大小数据。我们这里用一个额外的数组_size[]来表示。(一个集合的大小只保存在这个结合的根结点上_size[root] )
int _size[SIZE]//用来存储每个节点所在的集合大小
int _array[SIZE]//存储各个节点的集合的大小
void union(int i ,int j)
{
int rooti = root(i); //得到i的根节点
int rootj = root(j); //得到j的根结点
if( _size(rooti) > _size(rootj) ) //比较i属于的集合与j属于的集合的大小
{
_array(rootj) = _array(rooti); //如果i的集合较大,我们将j的根结点的父节点设置为i的根结点
_size(rooti) += _size(rootj); //更新合并后的新集合大小,一个集合的大小只保存在它的根结点
}
else
{
_array(rooti) = _array(rootj);
_size(rootj) += _size(rooti);
}
}运用平衡并查集之后,root()函数的时间复杂度可以达到近似O(lgn)的情况,如果画一张树状,并仔细观察合并的过程,可以很容易的推到出为什么会得到近似O(lgn)时的时间复杂度。这里简而言之就是只有到两个深度的集合(树)合并才能让合并的后的树的深度+1。由于上面我并没有太多用树的方法来说明并查集所以说出来有点抽象。
改进二 路径压缩:
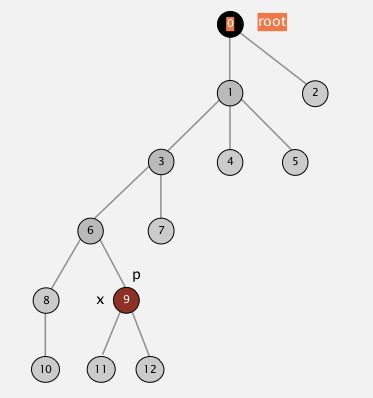
第二种改进,不得不说还是得从树的角度来阐述。看下面这张图。途中圆圈中的数字表明节点的索引,连线表明父子关系(在线段上方的为父节点)。
可以看到这个集合的深度为6。当我们对“11”节点执行root()操作的时候,我们会逐渐遍历它的父节点直到到达根结点0为止,比较次数为6与深度相等。
那么我们有不有办法使这个过程缩短呢?这就是我们接下来要提到的path compression(路径压缩)。当我们执行root()操作的时候我们将可以将我们遍历的每个父节点的父节点直接连接到根结点这样深度就得到压缩了。这个压缩操作一直执行下去的话我们会发现这个集合的深度最终将变为2层。
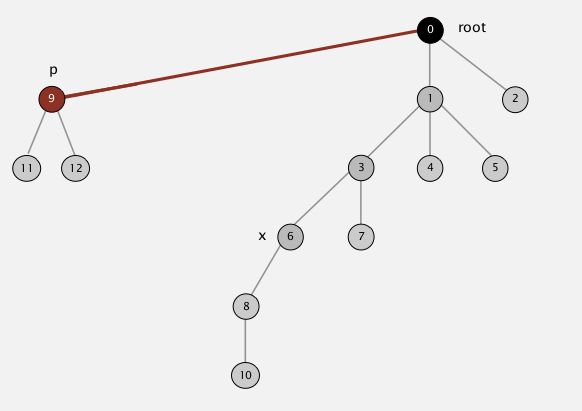
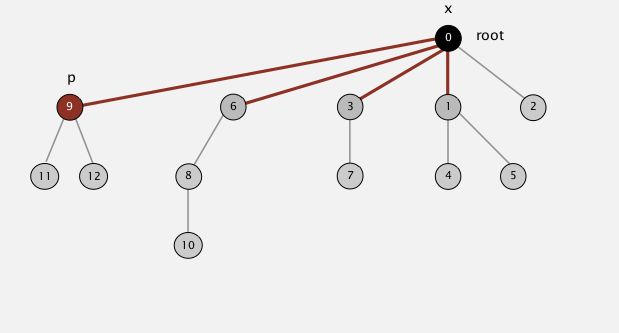
假设我们对"11"执行root()操作,第一个遍历的父节点为"9"如上图红点所示。我们将“9”的父节点直接设为根结点如下图
然后在接着第一副图的足迹遍历,下一个节点即是“6”,我们将“6”的父节点设置为根结点
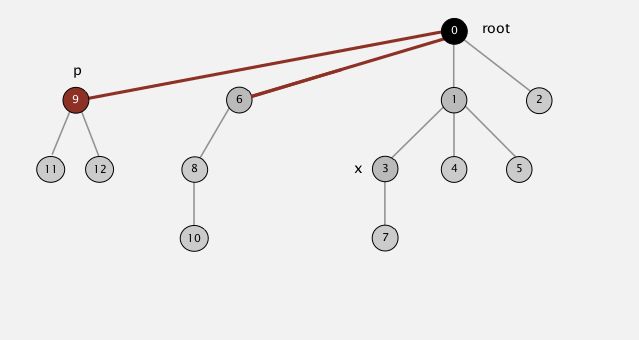
接着第一副图的足迹接下来是节点“3”,然后是节点“1”,到根结点“0”结束操作。最终操作如下
进行路径压缩虽然会逐渐减少集合(树)的深度,但是这个减少的过程本身也增加了root()操作的耗时。但是从总的来说这个消耗得到的收益随着union的大小增长也呈现飞速增长。来看看path compression的具体实现。
int root(int j)
{
int i = j;
while(i !=_array[i]) //根元素条件_array[i]=i
i =_array[i];
path_compression(i , j) //利用查找到的根结点i来对j的路径压缩
return i;
}
void path_compression(int root,int i)
{
while( i != _array[i] )
{
_array( _array[i] ) = root; //将遍历的父节点的父节点设为根结点
i = _array[i];
}
}这种path-compression 也即是我们上图所描述的path_compression,这种方法先搜索一次路径查找到根结点,然后利用查找到的根结点来进行路径压缩,即是搜索了两次路径。
还有一种只搜索路径一次便可以进行路径压缩的方法,这种压缩方法使路径中的父节点的父节点等于它的上一级的父节点(就像这个节点向上跳跃了一级),它的的压缩使路径深度减半。因为只搜索一次路径所以在时间上节约不少,但是压缩效果可能不如地一种。
int root(int j) //跟前面的方法一致
{
int i = j;
while(i !=_array[i]) //根元素条件_array[i]=i
{
_array[i] = _array[ array[i] ];//只增加了一行,使父节点的父节点指向它的上一级的父节点
i =_array[i];
}
return i;
}