Python深度学习之神经网络入门

Deep Learning with Python

这篇文章是我学习《Deep Learning with Python》(第二版，François Chollet 著) 时写的系列笔记之一。文章的内容是从 Jupyter notebooks 转成 Markdown 的，当我完成所以文章后，会在 GitHub 发布我写的所有 Jupyter notebooks。

你可以在这个网址在线阅读这本书的正版原文(英文)：https://livebook.manning.com/book/deep-learning-with-python

这本书的作者也给出了一套 Jupyter notebooks：https://github.com/fchollet/deep-learning-with-python-notebooks

---

本文为 第3章 神经网络入门 (Chapter 3. Getting started with neural networks) 的笔记整合。

本文目录：

电影评论分类:二分类问题

原文链接

IMDB 数据集

IMDB 数据集里是 50,000 条电影评论。一半是训练集，一半是测试集。
数据里 50% 是积极评价，50% 是消极评价。

Keras 内置了做过预处理的 IMDB 数据集，把单词序列转化成了整数序列（一个数字对应字典里的词）：

from tensorflow.keras.datasets import imdb

# 数据集
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(
    num_words=10000)

num_words=10000 是只保留出现频率前 10000 的单词。

先来随便看一条评论，这是条好评：

# 字典
index_word = {v: k for k, v in imdb.get_word_index().items()}

# 还原一条评论看看
text = ' '.join([index_word[i] for i in train_data[0]])

print(f"{train_labels[0]}:", text)

1: the as you with out themselves powerful lets loves their becomes reaching had journalist of lot from anyone to have after out atmosphere never more room and it so heart shows to years of every never going and help moments or of every chest visual movie except her was several of enough more with is now current film as you of mine potentially unfortunately of you than him that with out themselves her get for was camp of you movie sometimes movie that with scary but and to story wonderful that in seeing in character to of 70s musicians with heart had shadows they of here that with her serious to have does when from why what have critics they is you that isn't one will very to as itself with other and in of seen over landed for anyone of and br show's to whether from than out themselves history he name half some br of and odd was two most of mean for 1 any an boat she he should is thought frog but of script you not while history he heart to real at barrel but when from one bit then have two of script their with her nobody most that with wasn't to with armed acting watch an for with heartfelt film want an

数据准备

先看一下 train_data 现在的形状：

train_data.shape

输出：

(25000,)

我们要把它变成 (samples, word_indices) 的样子，大概是下面这种：

[[0, 0, ..., 1, ..., 0, ..., 1],
 [0, 1, ..., 0, ..., 1, ..., 0],
 ...
]

有这个词就是 1，没有就是 0。

import numpy as np

def vectorize_sequences(sequences, dimension=10000):
    results = np.zeros((len(sequences), dimension))
    for i, sequence in enumerate(sequences):
        results[i, sequence] = 1.
    return results

x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)

x_train

输出：

array([[0., 1., 1., ..., 0., 0., 0.],
       [0., 1., 1., ..., 0., 0., 0.],
       [0., 1., 1., ..., 0., 0., 0.],
       ...,
       [0., 1., 1., ..., 0., 0., 0.],
       [0., 1., 1., ..., 0., 0., 0.],
       [0., 1., 1., ..., 0., 0., 0.]])

labels 也随便搞一下：

train_labels

输出：

array([1, 0, 0, ..., 0, 1, 0])

处理一下：

y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')

y_train

输出：

array([1., 0., 0., ..., 0., 1., 0.], dtype=float32)

现在这些数据就可以安全投喂我们一会儿建的神经网络了。

建立网络

对于这种输入是向量、标签是标量（甚至是 0 或 1）的问题：
使用 relu 激活的 Dense (全连接)堆起来的网络：

Dense(16, activation='relu')

这种层的作用是 output = relu(dot(W, input) + b)。

16 是每层里隐藏单元(hidden unit)的个数。一个 hidden unit 就是在这层的表示空间里的一个维度。
W 的形状也是 (input_dimension, 16)，dot 出来就是个 16 维的向量，也就把数据投影到了 16 维的表示空间。

这个维度 (hidden unit 的数量) 可以看成对网络学习的自由度的控制。
维度越高，能学的东西越复杂，但计算消耗也越大，而且可能学到一些不重要的东西导致过拟合。

这里，我们将使用两层这种16个隐藏单元的层，
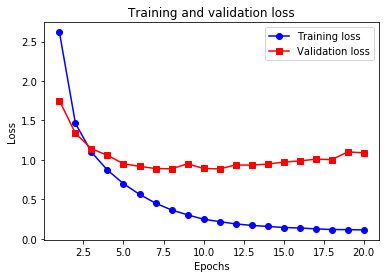
最后还有一个 sigmoid 激活的层来输出结果（在$[0,1]$内的值），
这个结果表示预测有多可能这个数据的标签是1，即一条好评。

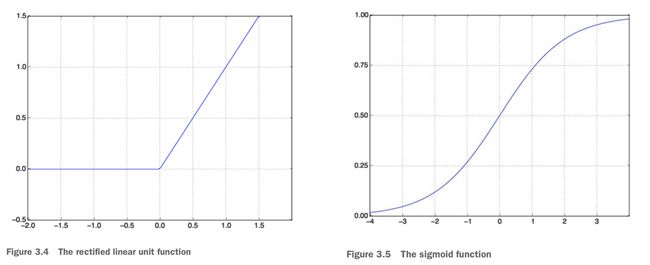
relu 是过滤掉负值（把输入的负值输出成0），sigmoid 是把值投到 [0, 1]：

在 Keras 中实现这个网络：

from tensorflow.keras import models
from tensorflow.keras import layers

model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000, )))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

激活函数的作用

我们之前在 MNIST 里用过 relu 激活函数，所以激活函数到底是干嘛的？

一个没有激活函数的 Dense 层的作用只是一个线性变换：

output = dot(W, input) + b

如果每一层都是这种线性变换，把多个这种层叠在一起，假设空间并不会变大，所以能学到的东西很有限。

而激活函数就是在 dot(W, input) + b 外面套的一个函数，比如 relu 激活是 output = relu(dot(W, input) + b)。
利用这种激活函数，可以拓展表示空间，也就可以让网络学习到更复杂的“知识”。

编译模型

编译模型时，我们还需要选择损失函数、优化器和指标。

对这种最后输出 0 或 1 的二元分类问题，损失函数可以使用 binary_crossentropy(从名字就可以看得出来很合适啦)。

这个 crossentropy 中文叫交叉熵，是信息论里的，是用来衡量概率分布直接的距离的。
所以输出概率的模型经常是用这种 crossentropy 做损失的。

至于优化器，和 MNIST 一样，我们用 rmsprop （书里还没写为什么），指标也还是准确度：

model.compile(optimizer='rmsprop',
              loss='binary_crossentropy',
              metrics=['accuracy'])

因为这几个optimizer、loss、metrics 都是常用的，所以 Keras 内置了，可以直接传字符串。
但也可以传类实例来定制一些参数：

from tensorflow.keras import optimizers
from tensorflow.keras import losses
from tensorflow.keras import metrics

model.compile(optimizer=optimizers.RMSprop(lr=0.001),
              loss=losses.binary_crossentropy,
              metrics=[metrics.binary_accuracy])

训练模型

为了在训练的过程中验证模型在它没见过的数据上精度如何，我们从原来的训练数据里分 10,000 个样本出来：

x_val = x_train[:10000]
partial_x_train = x_train[10000:]

y_val = y_train[:10000]
partial_y_train = y_train[10000:]

用一批 512 个样本的 mini-batches，跑 20 轮（所有x_train里的数据跑一遍算一轮），
并用刚分出来的 10,000 的样本做精度验证：

model.compile(optimizer='rmsprop',
              loss='binary_crossentropy',
              metrics=['acc'])

history = model.fit(partial_x_train,
                    partial_y_train,
                    epochs=20,
                    batch_size=512,
                    validation_data=(x_val, y_val))

Train on 15000 samples, validate on 10000 samples
Epoch 1/20
15000/15000 [==============================] - 3s 205us/sample - loss: 0.5340 - acc: 0.7867 - val_loss: 0.4386 - val_acc: 0.8340
.......
Epoch 20/20
15000/15000 [==============================] - 1s 74us/sample - loss: 0.0053 - acc: 0.9995 - val_loss: 0.7030 - val_acc: 0.8675

fit 阔以返回 history，里面保存了训练过程里每个 Epoch 的黑历史：

history_dict = history.history
history_dict.keys()

输出：

dict_keys(['loss', 'acc', 'val_loss', 'val_acc'])

我们可以把这些东西画图出来看：

# 画训练和验证的损失

import matplotlib.pyplot as plt

history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']

epochs = range(1, len(loss_values) + 1)

plt.plot(epochs, loss_values, 'ro-', label='Training loss')
plt.plot(epochs, val_loss_values, 'bs-', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()

plt.show()

# 画训练和验证的准确度

plt.clf()

acc = history_dict['acc']
val_acc = history_dict['val_acc']

plt.plot(epochs, acc, 'ro-', label='Training acc')
plt.plot(epochs, val_acc, 'bs-', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()

plt.show()

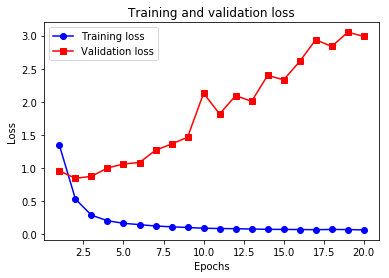
我们可以看到，训练集上的精度倒是一直在增（损失一直减），
但在验证集上，到了后面损失反而大了，差不多第4轮左右就到最好的峰值了。

这就是过拟合了，其实从第二轮开始就开始过了。所以，我们其实跑个3、4轮就 ok 了。
要是再跑下去，咱的模型就只“精通”训练集，不认识其他没见过的数据了。

所以，我们重新训练一个模型（要从建立网络开始重写，不然fit是接着刚才已经进行过的这些），那去用测试集测试：

model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000, )))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

model.compile(optimizer='rmsprop',
             loss='binary_crossentropy',
             metrics=['accuracy'])

model.fit(x_train, y_train, epochs=4, batch_size=512)
result = model.evaluate(x_test, y_test, verbose=2)    # verbose=2 to avoid a looooong progress bar that fills the screen with '='. https://github.com/tensorflow/tensorflow/issues/32286

Train on 25000 samples
Epoch 1/4
25000/25000 [==============================] - 2s 69us/sample - loss: 0.4829 - accuracy: 0.8179
Epoch 2/4
25000/25000 [==============================] - 1s 42us/sample - loss: 0.2827 - accuracy: 0.9054
Epoch 3/4
25000/25000 [==============================] - 1s 42us/sample - loss: 0.2109 - accuracy: 0.9253
Epoch 4/4
25000/25000 [==============================] - 1s 43us/sample - loss: 0.1750 - accuracy: 0.9380
25000/1 - 3s - loss: 0.2819 - accuracy: 0.8836

把结果输出出来看看：

print(result)

[0.2923990402317047, 0.8836]

训练完成后，我们当然想实际试一下，对吧。所以我们预测一下测试集，把结果打出来看看：

model.predict(x_test)

Output:

array([[0.17157233],
       [0.99989915],
       [0.79564804],
       ...,
       [0.11750051],
       [0.05890778],
       [0.5040823 ]], dtype=float32)

进一步实验

1. 尝试只用一个层

model = models.Sequential()
# model.add(layers.Dense(16, activation='relu', input_shape=(10000, )))
# model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid', input_shape=(10000, )))

model.compile(optimizer='rmsprop',
             loss='binary_crossentropy',
             metrics=['accuracy'])

model.fit(x_train, y_train, epochs=4, batch_size=512)
result = model.evaluate(x_test, y_test, verbose=2)    # verbose=2 to avoid a looooong progress bar that fills the screen with '='. https://github.com/tensorflow/tensorflow/issues/32286
print(result)

Train on 25000 samples
Epoch 1/4
25000/25000 [==============================] - 3s 116us/sample - loss: 0.5865 - accuracy: 0.7814
Epoch 2/4
25000/25000 [==============================] - 1s 31us/sample - loss: 0.4669 - accuracy: 0.8608
Epoch 3/4
25000/25000 [==============================] - 1s 32us/sample - loss: 0.3991 - accuracy: 0.8790
Epoch 4/4
25000/25000 [==============================] - 1s 33us/sample - loss: 0.3538 - accuracy: 0.8920
25000/1 - 3s - loss: 0.3794 - accuracy: 0.8732
[0.3726908649635315, 0.8732]

…这问题比较简单，一个层效果都这么好，但比之前正经的差远了

2. 多搞几个层

model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000, )))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

model.compile(optimizer='rmsprop',
             loss='binary_crossentropy',
             metrics=['accuracy'])

model.fit(x_train, y_train, epochs=4, batch_size=512)
result = model.evaluate(x_test, y_test, verbose=2)    # verbose=2 to avoid a looooong progress bar that fills the screen with '='. https://github.com/tensorflow/tensorflow/issues/32286
print(result)

Train on 25000 samples
Epoch 1/4
25000/25000 [==============================] - 3s 123us/sample - loss: 0.5285 - accuracy: 0.7614
Epoch 2/4
25000/25000 [==============================] - 1s 45us/sample - loss: 0.2683 - accuracy: 0.9072s - loss:
Epoch 3/4
25000/25000 [==============================] - 1s 45us/sample - loss: 0.1949 - accuracy: 0.9297
Epoch 4/4
25000/25000 [==============================] - 1s 47us/sample - loss: 0.1625 - accuracy: 0.9422
25000/1 - 2s - loss: 0.3130 - accuracy: 0.8806
[0.30894253887176515, 0.88056]

好一点，但也还不如正经的版本

3. 多几个隐藏层的单元

model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000, )))
model.add(layers.Dense(1024, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

model.compile(optimizer='rmsprop',
             loss='binary_crossentropy',
             metrics=['accuracy'])

model.fit(x_train, y_train, epochs=4, batch_size=512)
result = model.evaluate(x_test, y_test, verbose=2)    # verbose=2 to avoid a looooong progress bar that fills the screen with '='. https://github.com/tensorflow/tensorflow/issues/32286
print(result)

Train on 25000 samples
Epoch 1/4
25000/25000 [==============================] - 15s 593us/sample - loss: 0.5297 - accuracy: 0.7964
Epoch 2/4
25000/25000 [==============================] - 12s 490us/sample - loss: 0.2233 - accuracy: 0.9109
Epoch 3/4
25000/25000 [==============================] - 12s 489us/sample - loss: 0.1148 - accuracy: 0.9593
Epoch 4/4
25000/25000 [==============================] - 12s 494us/sample - loss: 0.0578 - accuracy: 0.9835
25000/1 - 9s - loss: 0.3693 - accuracy: 0.8812
[0.4772889766550064, 0.8812]

不是远多越好呀。

4. 用 mse 损失

model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000, )))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

model.compile(optimizer='rmsprop',
             loss='mse',
             metrics=['accuracy'])

model.fit(x_train, y_train, epochs=4, batch_size=512)
result = model.evaluate(x_test, y_test, verbose=2)    # verbose=2 to avoid a looooong progress bar that fills the screen with '='. https://github.com/tensorflow/tensorflow/issues/32286
print(result)

Train on 25000 samples
Epoch 1/4
25000/25000 [==============================] - 3s 119us/sample - loss: 0.1472 - accuracy: 0.8188
Epoch 2/4
25000/25000 [==============================] - 1s 46us/sample - loss: 0.0755 - accuracy: 0.9121
Epoch 3/4
25000/25000 [==============================] - 1s 50us/sample - loss: 0.0577 - accuracy: 0.9319
Epoch 4/4
25000/25000 [==============================] - 1s 47us/sample - loss: 0.0474 - accuracy: 0.9442
25000/1 - 3s - loss: 0.0914 - accuracy: 0.8828
[0.08648386991858482, 0.88276]

5. 用 tanh 激活

model = models.Sequential()
model.add(layers.Dense(16, activation='tanh', input_shape=(10000, )))
model.add(layers.Dense(16, activation='tanh'))
model.add(layers.Dense(1, activation='sigmoid'))

model.compile(optimizer='rmsprop',
             loss='binary_crossentropy',
             metrics=['accuracy'])

model.fit(x_train, y_train, epochs=4, batch_size=512)
result = model.evaluate(x_test, y_test, verbose=2)    # verbose=2 to avoid a looooong progress bar that fills the screen with '='. https://github.com/tensorflow/tensorflow/issues/32286
print(result)

Train on 25000 samples
Epoch 1/4
25000/25000 [==============================] - 4s 149us/sample - loss: 0.4237 - accuracy: 0.8241
Epoch 2/4
25000/25000 [==============================] - 1s 46us/sample - loss: 0.2310 - accuracy: 0.9163
Epoch 3/4
25000/25000 [==============================] - 1s 46us/sample - loss: 0.1779 - accuracy: 0.9329
Epoch 4/4
25000/25000 [==============================] - 1s 49us/sample - loss: 0.1499 - accuracy: 0.9458
25000/1 - 3s - loss: 0.3738 - accuracy: 0.8772
[0.3238203083658218, 0.87716]

所以，这些实验就是说，之前我们书上用的模型是合理的，你改来改去都不如他那个。

新闻分类: 多分类问题

原文链接

刚才我们电影评论问题不是把向量输入分成两类嘛，这节我们要把东西分成多类，即做“多分类（multi-class classification）”。

我们要把来自路透社的新闻分到 46 个话题种类里，这里要求一条新闻只能属于一个类，所以具体来说，我们要做的是一个“单标签多分类（single-label, multiclass classification）”问题。

路透社数据集

the Reuters dataset，路透社在 1986 年（比我老多了）发布的数据集，里面有 46 类新闻，训练集里每类至少 10 条数据。

这个玩具数据集和 IMDB、MNIST 一样，也在 Keras 里内置了：

from tensorflow.keras.datasets import reuters

(train_data, train_labels), (test_data, test_labels) = reuters.load_data(
    num_words=10000)

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/reuters.npz
2113536/2110848 [==============================] - 6s 3us/step

这个数据集里面的数据和之前的 IMDB 一样，把单词翻译成了数字，然后我们只截取出现频率最高的10000个词。

咱们这个训练集里有 8K+ 条数据，测试集 2K+：

print(len(train_data), len(test_data))

8982 2246

咱们还是像搞 IMDB 时那样，把数据还原会文本看看：

def decode_news(data):
    reverse_word_index = {v: k for k, v in reuters.get_word_index().items()}
    return ' '.join([reverse_word_index.get(i - 3, '?') for i in data])
    # i - 3 是因为 0、1、2 为保留词 “padding”(填充)、“start of sequence”(序列开始)、“unknown”(未知词)


text = decode_news(train_data[0])
print(text)

? ? ? said as a result of its december acquisition of space co it expects earnings per share in 1987 of 1 15 to 1 30 dlrs per share up from 70 cts in 1986 the company said pretax net should rise to nine to 10 mln dlrs from six mln dlrs in 1986 and rental operation revenues to 19 to 22 mln dlrs from 12 5 mln dlrs it said cash flow per share this year should be 2 50 to three dlrs reuter 3

标签是 0~45 的数字：

train_labels[0]

Output:

3

数据准备

首先，还是把数据位向量化，直接套用我们搞 IMDB 时写的代码：

import numpy as np

def vectorize_sequences(sequences, dimension=10000):
    results = np.zeros((len(sequences), dimension))
    for i, sequence in enumerate(sequences):
        results[i, sequence] = 1.
    return results


x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)

然后就是这种效果：

print(x_train)

array([[0., 1., 1., ..., 0., 0., 0.],
       [0., 1., 1., ..., 0., 0., 0.],
       [0., 1., 1., ..., 0., 0., 0.],
       ...,
       [0., 1., 1., ..., 0., 0., 0.],
       [0., 1., 1., ..., 0., 0., 0.],
       [0., 1., 1., ..., 0., 0., 0.]])

然后要处理标签。我们可以把标签处理成整数张量，也可以用 One-hot 编码
对于分类这种问题，我们常用 one-hot 编码（也叫分类编码，categorical encoding）。

对于我们当前的问题，使用 one-hot 编码，即用除了标签索引位置为 1 其余位置全为 0 的向量：

def to_one_hot(labels, dimension=46):
    results = np.zeros((len(labels), dimension))
    for i, label in enumerate(labels):
        results[i, label] = 1.
    return results


one_hot_train_labels = to_one_hot(train_labels)
one_hot_test_labels = to_one_hot(test_labels)

其实，，，Keras 里自带了一个可以干这个事情的函数：

from tensorflow.keras.utils import to_categorical
# 书上是 from keras.utils.np_utils import to_categorical 但，，，时代变了，而且咱这用的是 tensorflow.keras，所以稍微有点区别

one_hot_train_labels = to_categorical(train_labels)
one_hot_test_labels = to_categorical(test_labels)

print(one_hot_train_labels)

array([[0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.],
       ...,
       [0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.]], dtype=float32)

构建网络

这个问题和之前的电影评论分类问题还是差不多的，只是最后的解的可能从 2 -> 46，解空间大了太多了。

对于我们用的 Dense 层堆叠，每层都是接收上一层输出的信息作为输入。
所以，如果某一层丢失了一些信息，那么这些信息就再也不能被后面的层找回来了。
如果丢失的信息对分类没用，那这种丢失是好的、我们期望发生的；
但如果这些丢失的信息是对最后分类起作用的，那这种丢失就制约网络的结果了。
也就是说，这可能造成一种“信息瓶颈”。这种瓶颈在每一层都可能发生。

之前的电影评论分类最后只要 2 个结果，所以我们把层里的单元是用了 16 个，
即让机器在一个 16 维空间里学习，以及足够大了，不太会有“信息瓶颈“。

而我们现在的问题，解空间是 46 维的。
直接照搬之前的代码，让它在 16 维空间里学习，肯定有瓶颈！

解决瓶颈的办法很简单，直接增加层里的单元就好。这里我们是 16 -> 64:

from tensorflow.keras import models
from tensorflow.keras import layers

model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))

在最后一层，我们的输出是 46 维的，对应 46 种分类，
而这一层的激活函数是 softmax，和我们在训练 MNIST 时用的一样。

用 softmax 可以让网络输出在 46 种分类上的概率分布，即一个 46 维的向量，
其中第 i 个元素代表输入属于第 i 种分类的可能性，
并且这 46 个元素的总和为 1。

编译模型

编译模型，又要确定损失函数、优化器和优化的目标了。

• 损失函数，分类问题嘛，还是用“分类交叉熵” categorical_crossentropy。
• 优化器，其实对很多问题我们都是用 rmsprop
• 目标还是一个，预测的精度 accuracy

model.compile(optimizer='rmsprop',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

验证效果

我们还是要搞一个验证集来在训练过程中评估模型的。从训练集里分个 1K 条数据出来就好：

x_val = x_train[:1000]
partial_x_train = x_train[1000:]

y_val = one_hot_train_labels[:1000]
partial_y_train = one_hot_train_labels[1000:]

训练模型

好了，准备工作完成，又可以看到最迷人的训练过程了！

history = model.fit(partial_x_train,
                    partial_y_train,
                    epochs=20,
                    batch_size=512,
                    validation_data=(x_val, y_val))

Train on 7982 samples, validate on 1000 samples
Epoch 1/20
7982/7982 [==============================] - 3s 372us/sample - loss: 2.6180 - accuracy: 0.5150 - val_loss: 1.7517 - val_accuracy: 0.6290
......
Epoch 20/20
7982/7982 [==============================] - 1s 91us/sample - loss: 0.1134 - accuracy: 0.9578 - val_loss: 1.0900 - val_accuracy: 0.8040

挺快的，照例，还是画图看看训练过程。

1. 训练过程中的损失

import matplotlib.pyplot as plt

loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)

plt.plot(epochs, loss, 'bo-', label='Training loss')
plt.plot(epochs, val_loss, 'rs-', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

2. 训练过程中的精度

plt.clf()

acc = history.history['accuracy']
val_acc = history.history['val_accuracy']

plt.plot(epochs, acc, 'bo-', label='Training acc')
plt.plot(epochs, val_acc, 'rs-', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

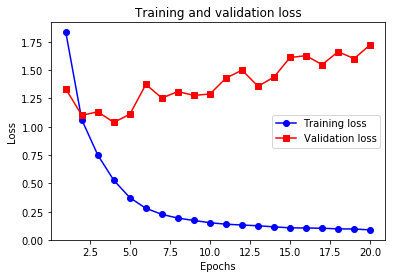
Emmmm，说，第9轮 epochs 的时候开始过拟合了（你看validation的曲线抖在第9轮了一下）。
所以只要跑 9 轮就够了。

model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))

model.compile(optimizer='rmsprop',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

model.fit(partial_x_train,
          partial_y_train,
          epochs=9,
          batch_size=512,
          validation_data=(x_val, y_val))

Train on 7982 samples, validate on 1000 samples
Epoch 1/9
7982/7982 [==============================] - 1s 153us/sample - loss: 2.5943 - accuracy: 0.5515 - val_loss: 1.7017 - val_accuracy: 0.6410
......
Epoch 9/9
7982/7982 [==============================] - 1s 84us/sample - loss: 0.2793 - accuracy: 0.9402 - val_loss: 0.8758 - val_accuracy: 0.8170

然后，用测试集测试一下:

results = model.evaluate(x_test, one_hot_test_labels, verbose=2)
print(results)

2246/1 - 0s - loss: 1.7611 - accuracy: 0.7912
[0.983459981976082, 0.7911843]

精度差不多 80%，其实还是不错的了，比随机瞎划线去分好多了。

如果随机划线去分类的话，对二元分类问题精度是 50 %，而对这 46 元的分类精度只要不到 19% 了：

import copy

test_labels_copy = copy.copy(test_labels)
np.random.shuffle(test_labels_copy)
hits_array = np.array(test_labels) == np.array(test_labels_copy)
float(np.sum(hits_array)) / len(test_labels)

0.18432769367764915

调用 model 实例的 predict 方法，可以得到对输入在 46 个分类上的概率分布：

predictions = model.predict(x_test)
print(predictions)

array([[4.7181980e-05, 2.0765587e-05, 8.6653872e-06, ..., 3.1266565e-05,
        8.2046267e-07, 6.0611728e-06],
       [5.9005950e-04, 1.3404934e-02, 1.2290048e-03, ..., 4.2919168e-05,
        5.7422225e-05, 4.0201416e-05],
       [8.5751421e-04, 9.2367262e-01, 1.5855590e-03, ..., 4.8341672e-04,
        4.5594123e-05, 2.6183401e-05],
       ...,
       [8.5679676e-05, 2.0081598e-04, 4.1808224e-05, ..., 7.6962686e-05,
        6.5783697e-06, 2.9889508e-05],
       [1.7291466e-03, 2.5600385e-02, 1.8182390e-03, ..., 1.4499390e-03,
        4.8478998e-04, 8.5257640e-04],
       [2.5776261e-04, 8.6797208e-01, 3.9900807e-03, ..., 2.6547859e-04,
        6.5820634e-05, 6.8603881e-06]], dtype=float32)

predictions 分别代表 46 个分类的可能:

predictions[0].shape

(46,)

他们的总和为 1：

np.sum(predictions[0])

0.99999994

其中最大的，即我们认为这条新闻属于这个分类

np.argmax(predictions[0])

3

处理标签和损失的另一种方法

前面提到了标签可以使用 one-hot 编码，或者直接把标签处理成整数张量：

y_train = np.array(train_labels)
y_test = np.array(test_labels)

用这种的话，损失函数也要跟着改，改成 sparse_categorical_crossentropy，
这个和 categorical_crossentropy 在数学上是一样的，只是接口不同：

 model.compile(optimizer='rmsprop',
               loss='sparse_categorical_crossentropy',
               metrics=['acc'])

中间层维度足够大的重要性

之前讨论了关于“信息瓶颈”的事，然后我们就说对这个 46 维结果的网络，中间层的维度要足够大！

现在咱试试如果不够大（导致信息瓶颈）会怎么样，咱搞夸张一点，从 64 减到 4：

model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(4, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))

model.compile(optimizer='rmsprop',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

model.fit(partial_x_train,
          partial_y_train,
          epochs=20,
          batch_size=128,
          validation_data=(x_val, y_val))

Train on 7982 samples, validate on 1000 samples
Epoch 1/20
7982/7982 [==============================] - 2s 288us/sample - loss: 2.8097 - accuracy: 0.4721 - val_loss: 2.0554 - val_accuracy: 0.5430
.......
Epoch 20/20
7982/7982 [==============================] - 1s 121us/sample - loss: 0.6443 - accuracy: 0.8069 - val_loss: 1.8962 - val_accuracy: 0.6800

看看这，这训练出来比之前 64 维的差的不是一点半点哈，差距相当明显了。

发生这种效果的下降就是因为你给他学习的空间维度太低了，他把好多对分类有用的信息抛弃了。

那是不是越大越好？我们再试试把中间层加大一些：

model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(4096, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))

model.compile(optimizer='rmsprop',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

model.fit(partial_x_train,
          partial_y_train,
          epochs=20,
          batch_size=128,
          validation_data=(x_val, y_val))

Train on 7982 samples, validate on 1000 samples
Epoch 1/20
7982/7982 [==============================] - 2s 273us/sample - loss: 1.5523 - accuracy: 0.6310 - val_loss: 1.1903 - val_accuracy: 0.7060
......
Epoch 20/20
7982/7982 [==============================] - 2s 296us/sample - loss: 0.0697 - accuracy: 0.9605 - val_loss: 3.5296 - val_accuracy: 0.7850

可以看到训练用的时间长了一点，电脑更暖手了一点，但效果却没有多大的提升。
这是由于第一层输入到中间层的只有 64 维嘛，中间层再大，也被第一层的瓶颈制约了。

在试试把第一层也加大！

model = models.Sequential()
model.add(layers.Dense(512, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(512, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))

model.compile(optimizer='rmsprop',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

model.fit(partial_x_train,
          partial_y_train,
          epochs=20,
          batch_size=128,
          validation_data=(x_val, y_val))

Train on 7982 samples, validate on 1000 samples
Epoch 1/20
7982/7982 [==============================] - 5s 662us/sample - loss: 1.3423 - accuracy: 0.6913 - val_loss: 0.9565 - val_accuracy: 0.7920
......
Epoch 20/20
7982/7982 [==============================] - 5s 583us/sample - loss: 0.0648 - accuracy: 0.9597 - val_loss: 2.9887 - val_accuracy: 0.8030

（稍微小一点，本来是用 4096 的，但太大了，咱乞丐版 mbp 跑的贼慢，跑完要20多分钟，我懒得等）

这个多浪费了好多时间，而且他很快就过泥河过拟合了，过得还过得很严重，画个图看一下：

import matplotlib.pyplot as plt

loss = _.history['loss']
val_loss = _.history['val_loss']
epochs = range(1, len(loss) + 1)

plt.plot(epochs, loss, 'bo-', label='Training loss')
plt.plot(epochs, val_loss, 'rs-', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

所以，太大了也不好。还是要有个度！

尝试使用更少/更多的层

1. 更少的层

model = models.Sequential()
model.add(layers.Dense(46, activation='softmax', input_shape=(10000,)))

model.compile(optimizer='rmsprop',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

history = model.fit(partial_x_train,
          partial_y_train,
          epochs=20,
          batch_size=128,
          validation_data=(x_val, y_val))

loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)

plt.plot(epochs, loss, 'bo-', label='Training loss')
plt.plot(epochs, val_loss, 'rs-', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

Train on 7982 samples, validate on 1000 samples
Epoch 1/20
7982/7982 [==============================] - 1s 132us/sample - loss: 2.4611 - accuracy: 0.6001 - val_loss: 1.8556 - val_accuracy: 0.6440
......
Epoch 20/20
7982/7982 [==============================] - 1s 85us/sample - loss: 0.1485 - accuracy: 0.9570 - val_loss: 1.2116 - val_accuracy: 0.7960

快呀！结果稍微差了一点点。

Clown0te("防盗文爬:)虫的追踪标签，读者不必在意").by(CDFMLR)

2. 更多的层

model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))

model.compile(optimizer='rmsprop',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

history = model.fit(partial_x_train,
          partial_y_train,
          epochs=20,
          batch_size=128,
          validation_data=(x_val, y_val))

loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)

plt.plot(epochs, loss, 'bo-', label='Training loss')
plt.plot(epochs, val_loss, 'rs-', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

Train on 7982 samples, validate on 1000 samples
Epoch 1/20
7982/7982 [==============================] - 2s 188us/sample - loss: 1.8340 - accuracy: 0.5829 - val_loss: 1.3336 - val_accuracy: 0.6910
......
Epoch 20/20
7982/7982 [==============================] - 1s 115us/sample - loss: 0.0891 - accuracy: 0.9600 - val_loss: 1.7227 - val_accuracy: 0.7900

所以，这个也不是越多越好呀！

预测房价: 回归问题

原文链接

前面两个例子，我们都是在做分类问题（预测离散的标签）。这次看一个回归问题（预测连续的数值）。

波士顿房间数据集

我们用 Boston Housing Price dataset 这个数据集来预测 70 年代中期的波士顿郊区房价。数据集里有当时那个地方的一些数据，比如犯罪律、税率什么的。

这个数据集比起我们前两个分类的数据集，数据相当少，只有 506 个，404 个在训练集，102 非个在测试集。数据里每种特征（feature）的输入数据数量级也不尽相同。

我们先把数据导进来看看（这个数据集也是 Keras 自带有的）：

from tensorflow.keras.datasets import boston_housing

(train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()

print(train_data.shape, test_data.shape)

(404, 13) (102, 13)

train_data[0:3]

array([[1.23247e+00, 0.00000e+00, 8.14000e+00, 0.00000e+00, 5.38000e-01,
        6.14200e+00, 9.17000e+01, 3.97690e+00, 4.00000e+00, 3.07000e+02,
        2.10000e+01, 3.96900e+02, 1.87200e+01],
       [2.17700e-02, 8.25000e+01, 2.03000e+00, 0.00000e+00, 4.15000e-01,
        7.61000e+00, 1.57000e+01, 6.27000e+00, 2.00000e+00, 3.48000e+02,
        1.47000e+01, 3.95380e+02, 3.11000e+00],
       [4.89822e+00, 0.00000e+00, 1.81000e+01, 0.00000e+00, 6.31000e-01,
        4.97000e+00, 1.00000e+02, 1.33250e+00, 2.40000e+01, 6.66000e+02,
        2.02000e+01, 3.75520e+02, 3.26000e+00]])

train_targets[0:3]

array([15.2, 42.3, 50. ])

targets 里的数据单位是 千美元， 这个时候的房价还比较便宜：

min(train_targets), sum(train_targets)/len(train_targets), max(train_targets)

(5.0, 22.395049504950496, 50.0)

import matplotlib.pyplot as plt

x = range(len(train_targets))
y = train_targets

plt.plot(x, y, 'o', label='data')
plt.title('House Prices')
plt.xlabel('train_targets')
plt.ylabel('prices')
plt.legend()
plt.show()

数据准备

我们喂给神经网络的数据值的范围不应该差距太大，虽然神经网络是可以处理差距大的数据的，但总归不太好。
对于这种差距大的数据，我们一般都会对每个特征做标准化（feature-wise normalization）。

具体的操作是对每个特征（输入数据矩阵的一列）减去该列的均值，再除以其标准差。
这样做完之后，数据会变成以 0 为中心的，有一个标准差的（标准差为 1 ）。

用 Numpy 可以很容易的做这个：

mean = train_data.mean(axis=0)
std = train_data.std(axis=0)

train_data -= mean
train_data /= std

test_data -= mean
test_data /= std

注意哈，对测试集的处理用的是训练集的均值和标准差。

处理完数据就可以构建网络、训练了（标签不用处理，比分类方便）

构建网络

数据越少，越容易过拟合，要减缓过拟合，可以使用比较小的网络。

比如，在这个问题中，我们使用一个只有两个隐藏层的网络，每个 64 单元：

from tensorflow.keras import models
from tensorflow.keras import layers

def build_model():
    model = models.Sequential()
    model.add(layers.Dense(64, activation="relu", input_shape=(train_data.shape[1], )))
    model.add(layers.Dense(64, activation="relu"))
    model.add(layers.Dense(1))
    
    model.compile(optimizer="rmsprop", loss="mse", metrics=["mae"])
    
    return model

网络的最后一层只有一个单元，并且没有激活函数（所以是个线性的层）。这种层是我们做连续单值回归问题的最后一步的标配。

如果加了激活函数，输出的值就会有范围限制，比如 sigmoid 会把值限制到 [0, 1]。没有激活函数，这个线性的层输出的值就没有限制了。

我们在编译模型时，使用的损失函数是 mse （mean squared error，均方误差）。这个函数返回预测和真实目标值的差的平方。回归问题多用这个损失。

然后我们还用了以前没用过的训练指标 —— mae（mean absolute error，平均绝对误差），这个东西是预测和真实目标的差的绝对值。

拟合验证 —— K-fold 验证

我们之前一直在做 —— 为了对网络进行评估，来调节网络参数(比如训练的轮数)，我们将数据划分为训练集和验证集。这一次，我们也需要这么做。
但有一点麻烦是，我们这次的数据太少了，所以分出来的验证集就很小（可能才有100条数据）。这种情况下，验证集选择的数据不同，可能对验证的结果有很大影响（即验证集的划分方式不同可能造成验证结果的方差很大），这种情况会影响我们对模型的验证。

在这种尴尬的境地，最佳实践是使用 K-fold 交叉验证（K折交叉验证）。

用 K-fold 验证，我们把数据分成 K 个部分（一般 k = 4 or 5），然后实例化 K 个独立的模型，每个用 K-1 份数据去训练，然后用剩余的一份去验证，最终模型的验证分数使用 K 个部分的平均值。

K-fold 验证的代码实现：

稍微改一下书上的例子，我们加一点用 TensorBoard 来可视化训练过程的代码。首先在 Jupyter Lab 笔记本里加载 tensorboard：

# Load the TensorBoard notebook extension
# TensorBoard 可以可视化训练过程
%load_ext tensorboard
# Clear any logs from previous runs
!rm -rf ./logs/ 

输出：

The tensorboard extension is already loaded. To reload it, use:
  %reload_ext tensorboard

然后开始写主要的代码：

import numpy as np
import datetime
import tensorflow as tf

k = 4
num_val_samples = len(train_data) // k
num_epochs = 100
all_scores = []

# 准备 TensorBoard
log_dir = "logs/fit/" + datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir=log_dir, histogram_freq=1)

for i in range(k):
    print(f'processing fold #{i} ({i+1}/{k})')
    
    # 准备验证数据
    val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
    val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
    
    # 准备训练数据
    partial_train_data = np.concatenate(
        [train_data[: i * num_val_samples],
         train_data[(i+1) * num_val_samples :]],
        axis=0)
    partial_train_targets = np.concatenate(
        [train_targets[: i * num_val_samples], 
         train_targets[(i+1) *  num_val_samples :]], 
        axis=0)
    
    #构建、训练模型
    model = build_model()
    model.fit(partial_train_data, partial_train_targets, 
              epochs=num_epochs, batch_size=1, verbose=0,
              callbacks=[tensorboard_callback])
    
    # 有验证集评估模型
    val_mse, val_mae = model.evaluate(val_data, val_targets, verbose=0)
    all_scores.append(val_mae)


np.mean(all_scores)

processing fold #0 (1/4)
processing fold #1 (2/4)
processing fold #2 (3/4)
processing fold #3 (4/4)

2.4046657

用下面这个命令可以在 Jupyter Lab 笔记本里显示 tensorboard：

%tensorboard --logdir logs/fit

它大概是这样的：

这个东西也可以直接在你的浏览器里直接打开 http://localhost:6006 得到。

刚才那个只是玩一下哈，现在我们改一下，迭代 500 轮（没独显的mbp跑这个好慢啊啊啊），把训练的结果记下来：

k = 4
num_val_samples = len(train_data) // k

num_epochs = 500
all_mae_histories = []

for i in range(k):
    print(f'processing fold #{i} ({i+1}/{k})')
    
    # 准备验证数据
    val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
    val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
    
    # 准备训练数据
    partial_train_data = np.concatenate(
        [train_data[: i * num_val_samples],
         train_data[(i+1) * num_val_samples :]],
        axis=0)
    partial_train_targets = np.concatenate(
        [train_targets[: i * num_val_samples], 
         train_targets[(i+1) *  num_val_samples :]], 
        axis=0)
    
    #构建、训练模型
    model = build_model()
    history = model.fit(partial_train_data, partial_train_targets,
                        validation_data=(val_data, val_targets),
                        epochs=num_epochs, batch_size=1, verbose=0)

    mae_history = history.history['val_mae']
    all_mae_histories.append(mae_history)


print("Done.")

processing fold #0 (1/4)
processing fold #1 (2/4)
processing fold #2 (3/4)
processing fold #3 (4/4)
Done.

画图：

average_mae_history = [
    np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]

import matplotlib.pyplot as plt

plt.plot(range(1, len(average_mae_history) + 1), average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()

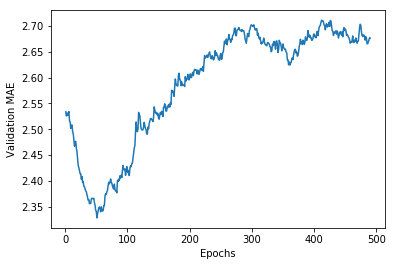
这个图太密了，看不清，所以要处理一下：

• 去掉前十组数据，这端明显和其他的数量差距比较大；
• 把每个点都换成前面数据点的指数移动平均值（an exponential moving average of the previous points），把曲线变平滑；

def smooth_curve(points, factor=0.9):
  smoothed_points = []
  for point in points:
    if smoothed_points:
      previous = smoothed_points[-1]
      smoothed_points.append(previous * factor + point * (1 - factor))
    else:
      smoothed_points.append(point)
  return smoothed_points

smooth_mae_history = smooth_curve(average_mae_history[10:])

plt.plot(range(1, len(smooth_mae_history) + 1), smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()

从这个图看，差不多过了 80 个 epochs 后就过拟合了。

在尝试了这些之后，我们找出最佳的参数（轮数啦，网络的层数啦，这些都可以试试），然后用最佳的参数在所有数据上训练，来得出最终的生产模型。

# 训练最终模型

model = build_model()
model.fit(train_data, train_targets, 
          epochs=80, batch_size=16, verbose=0)

# 最后评估一下
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets, verbose=0)
print(test_mse_score, test_mae_score)

17.43332971311083 2.6102107

这个 test_mae_score 的值说明，我们训练出来的模型的预测和实际大概差了 2k+ 美元。。。