Python深度学习之循环神经网络的高级用法
Deep Learning with Python
这篇文章是我学习《Deep Learning with Python》(第二版,François Chollet 著) 时写的系列笔记之一。文章的内容是从 Jupyter notebooks 转成 Markdown 的,你可以去 GitHub 或 Gitee 找到原始的 .ipynb 笔记本。
你可以去这个网站在线阅读这本书的正版原文(英文)。这本书的作者也给出了配套的 Jupyter notebooks。
本文为 第6章 深度学习用于文本和序列 (Chapter 6. Deep learning for text and sequences) 的笔记之一。
文章目录
- Deep Learning with Python
- 6.3 Advanced usage of recurrent neural networks
- 温度预测问题
- 数据准备
- 一种常识的、非机器学习的基准方法
- 机器学习基准方法
- 循环网络基准方法
- 循环 dropout
- 循环层的堆叠
- 双向 RNN
- Going even further
6.3 Advanced usage of recurrent neural networks
循环神经网络的高级用法
今回,我们通过一个实例,来了解循环神经网络的几个技巧:循环 dropout, 堆叠循环层,双向循环层。
温度预测问题
我们将使用某气象站记录的天气时间序列数据集(耶拿数据集),在这个数据集中,有每 10 分钟记录的 14 个量(比如气温、气压、湿度、风向等),这个数据集里有好多年的记录,这里我们只选用 2009—2016 年的。用这个数据集来构建模型,最后目标是输入最近的一些数据(几天的数据点),预测未来 24 小时的气温。
首先,下载并解压这个数据集:
cd ~/Somewhere
mkdir jena_climate
cd jena_climate
wget https://s3.amazonaws.com/keras-datasets/jena_climate_2009_2016.csv.zip
unzip jena_climate_2009_2016.csv.zip
看一下数据:
import os
data_dir = "/Volumes/WD/Files/dataset/jena_climate"
fname = os.path.join(data_dir, 'jena_climate_2009_2016.csv')
with open(fname) as f:
data = f.read()
lines = data.split('\n')
header = lines[0].split(',')
lines = lines[1:]
print(header)
print(len(lines))
print(lines[0])
['"Date Time"', '"p (mbar)"', '"T (degC)"', '"Tpot (K)"', '"Tdew (degC)"', '"rh (%)"', '"VPmax (mbar)"', '"VPact (mbar)"', '"VPdef (mbar)"', '"sh (g/kg)"', '"H2OC (mmol/mol)"', '"rho (g/m**3)"', '"wv (m/s)"', '"max. wv (m/s)"', '"wd (deg)"']
420551
01.01.2009 00:10:00,996.52,-8.02,265.40,-8.90,93.30,3.33,3.11,0.22,1.94,3.12,1307.75,1.03,1.75,152.30
把数据放到 Numpy 数组中:
import numpy as np
float_data = np.zeros((len(lines), len(header)-1))
for i, line in enumerate(lines):
values = [float(x) for x in line.split(',')[1:]]
float_data[i, :] = values
print(float_data.shape)
(420551, 14)
我们把气温的变化画出来,周期性很明显:
from matplotlib import pyplot as plt
temp = float_data[:, 1]
plt.plot(range(len(temp)), temp)
再看看前 10 天的数据(数据 10 分钟记一条,所以 1 天是 144 条):
plt.plot(range(1440), temp[: 1440])
这个图可以看出是个冬天的,每天的气温变化也是有周期性的(后面几天比较明显)。
接下来就要开始尝试做预测模型的工作了。首先明确一下我们的问题:给定过去 lookback 个时间步(10分钟一个),我们没 steps 步采样一次,让你去预测未来 delay 时间步的气温:
lookback = 720: 过去5天的观察数据steps = 6: 每小时采样一次观察数据delay = 144: 目标是未来24小时
数据准备
- 数据标准化:让各种特征在数量上差距不大
# 数据标准化
mean = float_data[:200000].mean(axis=0)
float_data -= mean
std = float_data[:200000].std(axis=0)
float_data /= std
- 把数据放到一个生成器,yield 出
(samples, targets),samples 是输入的数据批,targets 是对应的目标温度数组。
# 生成时间序列样本及其目标的生成器
def generator(data, # 原始数据
lookback, # 输入数据包括过去多少个时间步
delay, # 目标是未来的多少个时间步
min_index, max_index, # 指定从 data 的那个部分抽取
shuffle=False, # 打乱样本 or 按顺序抽取
batch_size=128, # 每批的样本数
step=6): # 数据采样的周期
if max_index is None:
max_index = len(data) - delay - 1
i = min_index + lookback
while True:
if shuffle:
rows = np.random.randint(min_index + lookback, max_index, size=batch_size)
else:
if i + batch_size >= max_index:
i = min_index + lookback
rows = np.arange(i, min(i + batch_size, max_index))
i += len(rows)
samples = np.zeros((len(rows), lookback // step, data.shape[-1]))
targets = np.zeros((len(rows), ))
for j, row in enumerate(rows):
indices = range(rows[j] - lookback, rows[j], step)
samples[j] = data[indices]
targets[j] = data[rows[j] + delay][1]
yield samples, targets
调用这个生成器,实例化训练集生成器、验证集生成器、测试集生成器:
# 准备训练生成器、验证生成器和测试生成器
lookback = 1440
step = 6
delay = 144
batch_size = 128
train_gen = generator(float_data,
lookback=lookback,
delay=delay,
min_index=0,
max_index=200000,
shuffle=True,
step=step,
batch_size=batch_size)
val_gen = generator(float_data,
lookback=lookback,
delay=delay,
min_index=200001,
max_index=300000,
step=step,
batch_size=batch_size)
test_gen = generator(float_data,
lookback=lookback,
delay=delay,
min_index=300001,
max_index=None,
step=step,
batch_size=batch_size)
# 验证和测试需要抽取多少次:
val_steps = (300000 - 200001 - lookback) // batch_size
test_steps = (len(float_data) - 300001 - lookback) // batch_size
一种常识的、非机器学习的基准方法
我们假设温度的时间序列是连续的,并且每天的温度是周期性变化的。这种情况下,可以大胆假设未来 24 小时的温度等于当前的温度。
我们就以此基于常识的非机器学习方法作为基准,用平均绝对误差(MAE)为指标来评估衡量它:
mae = np.mean(np.abs(preds - targets))
我们之后做的机器学习模型应该超过这个基准,才能说明机器学习是有效的。
# 计算基于常识的基准方法的 MAE
def evaluate_naive_method():
batch_maes = []
for step in range(val_steps):
samples, targets = next(val_gen)
preds = samples[:, -1, 1]
mae = np.mean(np.abs(preds - targets))
batch_maes.append(mae)
return np.mean(batch_maes)
mae = evaluate_naive_method()
celsius_mae = mae * std[1]
print(f'mae={mae}, 温度的平均绝对误差={celsius_mae}°C')
mae=0.2897359729905486, 温度的平均绝对误差=2.564887434980494°C
这个误差还是比较大的,所以接下来的目标就是用深度学习的方法来超过这个基准。
机器学习基准方法
在用复杂的、计算代价高的网络(比如 RNN)之前,最好先尝试一下简单的模型能否解决问题。
所以这里我们先用一个简单的全连接网络来尝试处理天气预测问题:
# plot_acc_and_loss: 绘制训练历史的实用函数
import matplotlib.pyplot as plt
def plot_acc_and_loss(history):
epochs = range(len(history.history['loss']))
try:
acc = history.history['acc']
val_acc = history.history['val_acc']
plt.plot(epochs, acc, 'bo-', label='Training acc')
plt.plot(epochs, val_acc, 'rs-', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
except:
print('No acc. Skip')
finally:
plt.figure()
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.plot(epochs, loss, 'bo-', label='Training loss')
plt.plot(epochs, val_loss, 'rs-', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
from tensorflow.keras.models import Sequential
from tensorflow.keras import layers
from tensorflow.keras.optimizers import RMSprop
model = Sequential()
model.add(layers.Flatten(input_shape=(lookback // step, float_data.shape[-1])))
model.add(layers.Dense(32, activation='relu'))
model.add(layers.Dense(1))
model.compile(optimizer=RMSprop(), loss='mae')
history = model.fit_generator(train_gen,
steps_per_epoch=500,
epochs=20,
validation_data=val_gen,
validation_steps=val_steps)
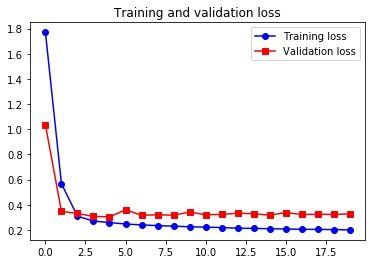
plot_acc_and_loss(history)
Epoch 1/20
500/500 [==============================] - 10s 20ms/step - loss: 1.7705 - val_loss: 1.0356
Epoch 2/20
500/500 [==============================] - 11s 21ms/step - loss: 0.5680 - val_loss: 0.3472
...
Epoch 19/20
500/500 [==============================] - 10s 21ms/step - loss: 0.2027 - val_loss: 0.3235
Epoch 20/20
500/500 [==============================] - 11s 22ms/step - loss: 0.2001 - val_loss: 0.3275
虽然这个结果里有一部分超过了不机器学习的基准方法,但不够可靠。事实上,要超越基于尝试的基准方法是不容易的,我们的尝试中包含了很多机器难以学到的有用的信息。一般来说,对这种用简单高效解的问题来说,除非我们硬编码让模型去使用这种简单方法,否则靠机器去学习参数是很难找到这个简单模型并进一步改进的。
循环网络基准方法
刚才的全连接网络一开始就用一个 Flatten 把时间序列展平了,所以那个模型实际上是没有考虑『时间』的概念的。要利用起时间的顺序,我们就可以考虑使用循环网络。这次,我们将使用 GRU 层而不是 LSTM:
# 训练并评估一个基于 GRU 的模型
from tensorflow.keras.models import Sequential
from tensorflow.keras import layers
from tensorflow.keras.optimizers import RMSprop
model = Sequential()
model.add(layers.GRU(32, input_shape=(None, float_data.shape[-1])))
model.add(layers.Dense(1))
model.compile(optimizer=RMSprop(), loss='mae')
history = model.fit_generator(train_gen,
steps_per_epoch=500,
epochs=20,
validation_data=val_gen,
validation_steps=val_steps)
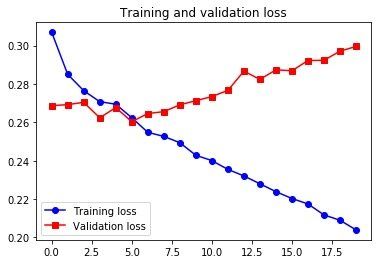
plot_acc_and_loss(history)
Epoch 1/20
500/500 [==============================] - 58s 116ms/step - loss: 0.3069 - val_loss: 0.2687
Epoch 2/20
500/500 [==============================] - 56s 113ms/step - loss: 0.2850 - val_loss: 0.2692
...
Epoch 19/20
500/500 [==============================] - 62s 124ms/step - loss: 0.2090 - val_loss: 0.2971
Epoch 20/20
500/500 [==============================] - 64s 128ms/step - loss: 0.2039 - val_loss: 0.2995
在开始过拟合之前,最好的结果的温度误差是:
print(0.2624 * std[1], '°C')
2.3228957591704926 °C
比一开始的常识模型优秀了。但我们看到,后面过拟合了,在 RNN 里,我们可以用循环 dropout 来对抗过拟合。
循环 dropout
我们在前馈网络里面使用 dropout,就是将某一层的输入单元随机得设为0。但在 RNNs 里没有那么简单,在循环层之前使用 dropout 只会阻碍学习,而对结果没有帮助,所以要在循环层中使用 droput。
在循环层中使用 dropout 必须对每个 timestep 使用相同的 mask(掩码,即舍弃单元),掩码不能随 timestep 的改变而有所不同。同时,对于 LSTM、GRU 等循环层,还要将一个不随时间改变的『循环 dropout 掩码』作用于层的内部循环激活。Keras 的 循环层中都内置了这两种 dropout 的实现,只需通过参数 dropout 和 recurrent_dropout 指定 dropout 的比例即可。
# 训练并评估一个使用 dropout 正则化的基于 GRU 的模型
from tensorflow.keras.models import Sequential
from tensorflow.keras import layers
from tensorflow.keras.optimizers import RMSprop
model = Sequential()
model.add(layers.GRU(32,
dropout=0.4,
recurrent_dropout=0.4,
input_shape=(None, float_data.shape[-1])))
model.add(layers.Dense(1))
model.compile(optimizer=RMSprop(), loss='mae')
history = model.fit_generator(train_gen,
steps_per_epoch=500,
epochs=40, # 使用了 dropout 的网络需要更长的时间才能收敛
validation_data=val_gen,
validation_steps=val_steps)
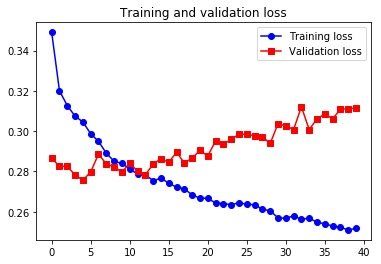
plot_acc_and_loss(history)
Epoch 1/40
500/500 [==============================] - 101s 202ms/step - loss: 0.3491 - val_loss: 0.2865
Epoch 2/40
500/500 [==============================] - 90s 180ms/step - loss: 0.3200 - val_loss: 0.2826
...
Epoch 39/40
500/500 [==============================] - 98s 196ms/step - loss: 0.2510 - val_loss: 0.3111
Epoch 40/40
500/500 [==============================] - 101s 202ms/step - loss: 0.2517 - val_loss: 0.3115
这个做出来没有书上好,不知道为什么。
循环层的堆叠
解决了过拟合的问题,现在要进一步提高精度。刚才只用了一个循环层,可以考虑再加几个,堆叠起来,增加网络容量。实际上,循环层的堆叠不用堆的特别多,谷歌翻译也只用了7个超大的LSTM层堆叠在一起。
在 Keras 中堆叠循环层,记得中间层应该返回完整的 3D 输出序列张量,不能只返回最后一个时间步的输出(这个行为是默认的):
from tensorflow.keras.models import Sequential
from tensorflow.keras import layers
from tensorflow.keras.optimizers import RMSprop
model = Sequential()
model.add(layers.GRU(32,
dropout=0.1,
recurrent_dropout=0.5,
return_sequences=True, # 输出完整输出序列
input_shape=(None, float_data.shape[-1])))
model.add(layers.GRU(64, activation='relu',
dropout=0.1,
recurrent_dropout=0.5))
model.add(layers.Dense(1))
model.compile(optimizer=RMSprop(), loss='mae')
history = model.fit_generator(train_gen,
steps_per_epoch=500,
epochs=40,
validation_data=val_gen,
validation_steps=val_steps)
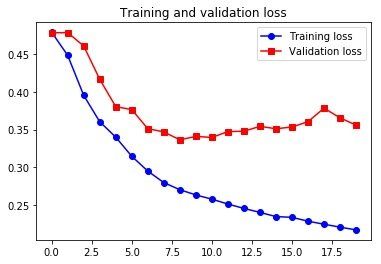
plot_acc_and_loss(history)
Epoch 1/40
500/500 [==============================] - 225s 450ms/step - loss: 0.3214 - val_loss: 0.2784
Epoch 2/40
500/500 [==============================] - 229s 459ms/step - loss: 0.3029 - val_loss: 0.2721
...
Epoch 39/40
500/500 [==============================] - 229s 458ms/step - loss: 0.1840 - val_loss: 0.3365
Epoch 40/40
500/500 [==============================] - 219s 438ms/step - loss: 0.1839 - val_loss: 0.3343
这个也和书上有所差距。但可以看出,堆叠循环层并没有带来太多的性能提升。
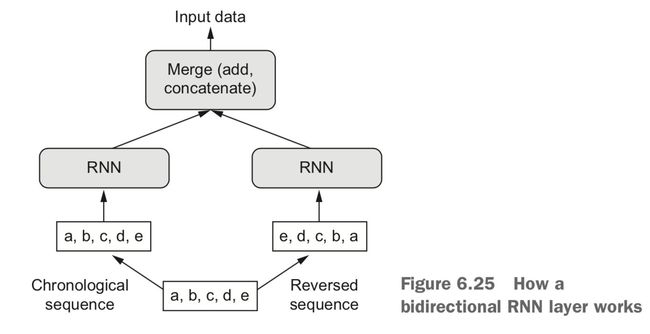
双向 RNN
Bidirectional RNNs (双向循环网络) 是 RNN 的变种,有时可以比 RNN 性能更好,尤其是在自然语言处理上,双向 RNN 被称为深度学习 NLP 的瑞士军队。
RNN 是依赖于序列的时间或者其他顺序的,打乱或反转时间步,RNN 从序列中提取的表示就完全不同了。利用了 RNN 对顺序的这种敏感性,双向 RNN 包含两个普通 RNN,分别沿正序和逆序对输入序列进行处理,最后将它们学到的表示合在一起,这样就可能学习到被单向 RNN 忽略的模式。
之前,我们默认按时间顺序去训练,现在我们可以试试逆序去处理。要逆序,只需在数据生成器最后方向输出就行了 yield samples[:, ::-1, :], targets):
def reverse_order_generator(data, lookback, delay, min_index, max_index,
shuffle=False, batch_size=128, step=6):
if max_index is None:
max_index = len(data) - delay - 1
i = min_index + lookback
while 1:
if shuffle:
rows = np.random.randint(
min_index + lookback, max_index, size=batch_size)
else:
if i + batch_size >= max_index:
i = min_index + lookback
rows = np.arange(i, min(i + batch_size, max_index))
i += len(rows)
samples = np.zeros((len(rows),
lookback // step,
data.shape[-1]))
targets = np.zeros((len(rows),))
for j, row in enumerate(rows):
indices = range(rows[j] - lookback, rows[j], step)
samples[j] = data[indices]
targets[j] = data[rows[j] + delay][1]
yield samples[:, ::-1, :], targets
train_gen_reverse = reverse_order_generator(
float_data,
lookback=lookback,
delay=delay,
min_index=0,
max_index=200000,
shuffle=True,
step=step,
batch_size=batch_size)
val_gen_reverse = reverse_order_generator(
float_data,
lookback=lookback,
delay=delay,
min_index=200001,
max_index=300000,
step=step,
batch_size=batch_size)
model = Sequential()
model.add(layers.GRU(32, input_shape=(None, float_data.shape[-1])))
model.add(layers.Dense(1))
model.compile(optimizer=RMSprop(), loss='mae')
history = model.fit_generator(train_gen_reverse,
steps_per_epoch=500,
epochs=20,
validation_data=val_gen_reverse,
validation_steps=val_steps)
plot_acc_and_loss(history)
Epoch 1/20
500/500 [==============================] - 61s 121ms/step - loss: 0.4796 - val_loss: 0.4788
Epoch 2/20
500/500 [==============================] - 58s 117ms/step - loss: 0.4488 - val_loss: 0.4791
...
Epoch 19/20
500/500 [==============================] - 57s 114ms/step - loss: 0.2202 - val_loss: 0.3657
Epoch 20/20
500/500 [==============================] - 57s 114ms/step - loss: 0.2165 - val_loss: 0.3560
这个效果并不好。是这样的,对于气温预测,当然是近期的数据比较有用、而很长时间之前的信息意义不大,循环层随着 timesteps 的前进会丢失一些老的信息,所以这个问题用正序的结果比逆序的结果好。
但对于文本信息的处理,一个单词对理解句子的重要性通常并不取决于它在句子中的位置。也就是说,虽然单词顺序对理解语言很重要,但使用哪种顺序并不重要。所以,在处理一些文本问题时,正序和逆序可能得到很类似的结果:
from tensorflow.keras.datasets import imdb
from tensorflow.keras.preprocessing import sequence
from tensorflow.keras import layers
from tensorflow.keras.models import Sequential
# Number of words to consider as features
max_features = 10000
# Cut texts after this number of words (among top max_features most common words)
maxlen = 500
# Load data
(x_train, y_train), (x_test, y_test) = imdb.load_data(num_words=max_features)
# Reverse sequences
x_train = [x[::-1] for x in x_train]
x_test = [x[::-1] for x in x_test]
# Pad sequences
x_train = sequence.pad_sequences(x_train, maxlen=maxlen)
x_test = sequence.pad_sequences(x_test, maxlen=maxlen)
model = Sequential()
model.add(layers.Embedding(max_features, 128))
model.add(layers.LSTM(32))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit(x_train, y_train,
epochs=10,
batch_size=128,
validation_split=0.2)
plot_acc_and_loss(history)
Epoch 1/10
157/157 [==============================] - 53s 339ms/step - loss: 0.4945 - acc: 0.7638 - val_loss: 0.4783 - val_acc: 0.8256
Epoch 2/10
157/157 [==============================] - 54s 345ms/step - loss: 0.3198 - acc: 0.8755 - val_loss: 0.5395 - val_acc: 0.7596
...
Epoch 9/10
157/157 [==============================] - 54s 344ms/step - loss: 0.1241 - acc: 0.9590 - val_loss: 0.4496 - val_acc: 0.8566
Epoch 10/10
157/157 [==============================] - 55s 352ms/step - loss: 0.1178 - acc: 0.9600 - val_loss: 0.4134 - val_acc: 0.8720
这个逆序训练的 IMDB 结果和正序的区别不大。
如果我们把正序和逆序结合起来,从不同的视角去查看数据,相互补充被彼此忽略的内容,就有可能提高模型的性能。这就是双向 RNN 要做的事。
在 Keras 中,使用 Bidirectional 层来实现双向 RNN:
# 在 IMDB 上训练并评估一个双向 LSTM
model = Sequential()
model.add(layers.Embedding(max_features, 32))
model.add(layers.Bidirectional(layers.LSTM(32)))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
history = model.fit(x_train, y_train, epochs=10, batch_size=128, validation_split=0.2)
plot_acc_and_loss(history)
Epoch 1/10
157/157 [==============================] - 50s 317ms/step - loss: 0.5840 - acc: 0.6994 - val_loss: 0.4705 - val_acc: 0.7818
Epoch 2/10
157/157 [==============================] - 45s 285ms/step - loss: 0.3490 - acc: 0.8637 - val_loss: 0.4346 - val_acc: 0.7974
...
Epoch 9/10
157/157 [==============================] - 45s 288ms/step - loss: 0.1411 - acc: 0.9537 - val_loss: 0.4225 - val_acc: 0.8778
Epoch 10/10
157/157 [==============================] - 45s 289ms/step - loss: 0.1249 - acc: 0.9589 - val_loss: 0.6158 - val_acc: 0.8424
接下来,我们尝试将双向 RNN 的方法应用于温度预测任务。
from tensorflow.keras.models import Sequential
from tensorflow.keras import layers
from tensorflow.keras.optimizers import RMSprop
model = Sequential()
model.add(layers.Bidirectional(
layers.GRU(32), input_shape=(None, float_data.shape[-1])))
model.add(layers.Dense(1))
model.compile(optimizer=RMSprop(), loss='mae')
history = model.fit_generator(train_gen,
steps_per_epoch=500,
epochs=40,
validation_data=val_gen,
validation_steps=val_steps)
plot_acc_and_loss(history)
Epoch 1/40
500/500 [==============================] - 81s 163ms/step - loss: 0.3022 - val_loss: 0.2796
Epoch 2/40
500/500 [==============================] - 76s 151ms/step - loss: 0.2761 - val_loss: 0.2619
...
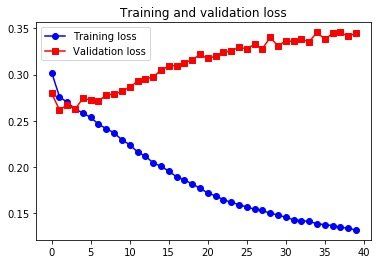
Epoch 39/40
500/500 [==============================] - 76s 152ms/step - loss: 0.1338 - val_loss: 0.3413
Epoch 40/40
500/500 [==============================] - 76s 152ms/step - loss: 0.1322 - val_loss: 0.3445
Going even further
接下来还可以通过尝试,更进一步提高模型的能力:
- 增加层的单元个数
- 调节 RMSprop 的学习率
- 尝试用 LSTM 层代替 GRU 层
- 在循环层上面(后面)使用更大的密集连接回归器(更大的 Dense 层或 Dense 层的堆叠)
- 在测试集上运行性能最佳的模型,防止模型对验证集过拟合
最后,温馨提示:不要用这个搞气温预测的方法去预测证券价格哦。在市场上,过去的表现并不能很好地预测未来的收益:Looking in the rear-view mirror is a bad way to drive.