【Java算法】分治算法

1.什么是分治算法？

分治法(Divide-and-Conquer)是一种很重要的算法。

分治就是“分而治之”的意思，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)，以及汉诺塔等等。

2.分治法的步骤

分治算法用递归来实现，而 在每一层递归上都有三个步骤：

• 分解：将原问题分解为若干个规模较小，相互独立且与原问题形式相同的子问题
• 解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题
• 合并：将各个子问题的解合并为原问题的解。

3.分治法的设计模式如下：

if |P|≤n0
   then return(ADHOC(P))
//将P分解为较小的子问题 P1 ,P2 ,…,Pk
for i←1 to k
do yi ← Divide-and-Conquer(Pi)   递归解决Pi
T ← MERGE(y1,y2,…,yk)   合并子问题
return(T)

其中|P|表示问题P的规模；n0为一阈值，表示当问题P的规模不超过n0时，问题已容易直接解出，不必再继续分解。

ADHOC(P)是该分治法中的基本子算法，用于直接解小规模的问题P。因此，当P的规模不超过n0时直接用算法ADHOC(P)求解。

算法MERGE(y1,y2,…,yk)是该分治法中的合并子算法，用于将P的子问题P1 ,P2 ,…,Pk的相应的解y1,y2,…,yk合并为P的解。

4.分治算法经典例子——-汉诺塔

汉诺塔问题：如图有A、B、C三个柱子，要求把A柱子上的圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

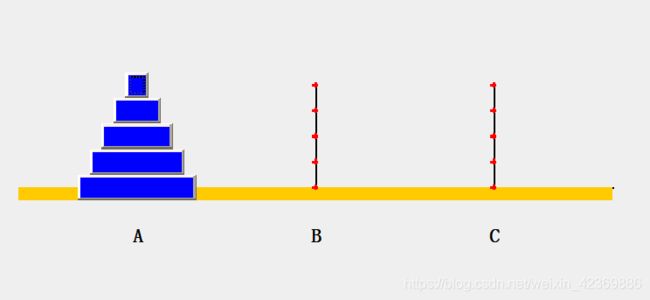
当A柱子上有两个盘子时，我们先把上面的小圆盘移动到B柱子，再把大圆盘移动到C柱子，最后把B柱子上的圆盘移动到C就完成了。当A的圆盘上越多时，问题就越难解决，我们可以借助分治法来解决。

分：

我们可以把汉诺塔游戏看成是两种情况：
情况1：如果是有一个盘， 我们直接从A移动到C即A->C；
情况2：如果我们有 n >= 2 情况，我们总是可以看做是两个盘 ：第一个盘是最下边的第n个盘 ，第二个盘是上面的（n-1）个盘。

治：

当我们把n>=2看成是两个盘时，我们就应该这么解决：
1）先把 最上面的盘从A移动到B即 A->B；
2）把最下边的盘 从A移动到C即A->C；
3）把B塔的所有盘 从 B移动到C即B->C；

5.汉诺塔代码实现：

public class HanoiTower {
    public static void main(String[] args) {
        //测试3个盘子
        hanoiTower(3,'A','B','C');
    }

    private static void hanoiTower(int i, char a, char b, char c) {
    //如果只有一个盘
        if(i==1){
	            System.out.println("第1个盘"+a+"->"+c);
        }else{
            //n>=2的情况
            //1.先把最上面的所有盘从A->B，移动过程会使用到c
            hanoiTower(i-1,a,c,b);
            //把最下边的盘从A->C
            System.out.println("第"+i+"个盘从"+a+"->"+c);
            //3.把B塔的所有盘从B->C,移动过程使用到a
            hanoiTower(i-1,b,a,c);
        }
    }
}

如果关于递归、快排、归并排序不太懂，可以看我写的文章：
递归文章：https://blog.csdn.net/weixin_42369886/article/details/104691381
快速排序文章：https://blog.csdn.net/weixin_42369886/article/details/104816252
归并排序文章：https://blog.csdn.net/weixin_42369886/article/details/104834635