基于Huffman算法和LZ77算法的文件压缩的改进方向

基于Huffman算法和LZ77算法的文件压缩（八）

到这里已经简单实现基于Huffman算法和LZ77算法的文件压缩，

GitHub源码：点我

根据基于Huffman算法和LZ77算法的文件压缩（七）已经介绍当前项目的缺陷及改进方法。

那么本文只讲思想，不实现。

一、范式Huffman树

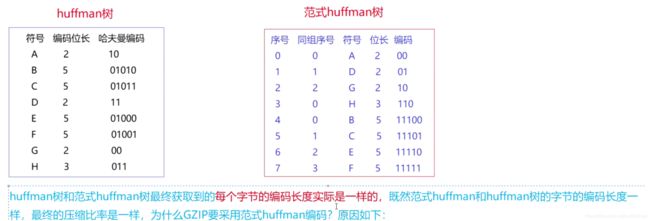
范式huffman树是在huffman树的基础之上，进行了一些强制性的约定，即：对于同一层节点中，所有的 叶子节点都调整到左边，然后，对于同一层的叶子节点按照符号顺序从小到大调整 ，最后按照左0右1的方式 分配编码。大家仔细观察下图：

从上表中可以得出一些结论：

1. 只要知道一个符号的编码位长就可以知道它在范式树上的位置。即：码表中只要保存每个符号的编码长 度(即节点在树中的高度)即可，其远远要比符号频度小。
2. 相同位长的编码之间都相差1
3. 第n层的编码可以根据上层算出来：code = (code + count[n-1])<<1;

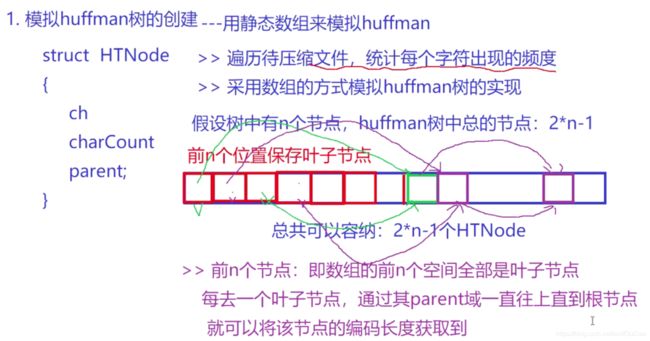
范式huffman树该如何创建呢？ 范式huffman树根本不用创建，可以利用huffman树推到出来：

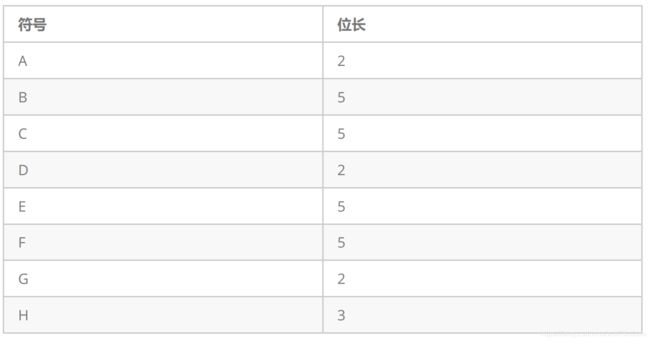
1. 对huffman树中的每个叶子节点求层数，得出huffman码表
2. 对huffman码表按照：码长(节点在树中的高度)为第一关键字、符号为第二关键字进行排序

通过以上两步就可以得出范式huffman树的码表，然后按照上面的公式既可以计算出范式huffman码表。

二、 基于范式huffman树的压缩与解压缩

1 压缩

1. 通过前面介绍的方式计算出huffman码表，并推算出每个字符的范式huffman编码
2. 读取源文件，将源文件中的每个字节按照对应的范式huffman编码进行改写

压缩文件的格式：

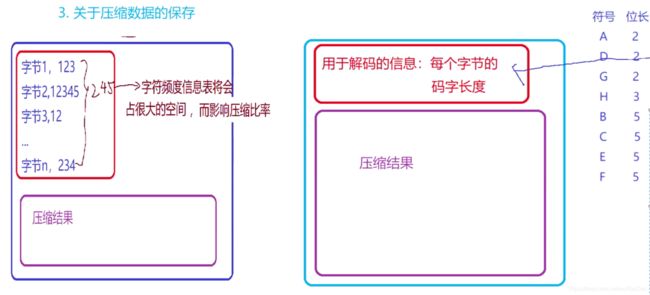
1. 先保存各个字节对应的码字长度(huffman压缩中保存的是符号及符号出现的频率)
2. 保存压缩数据

2 解压缩

1. 从压缩数据中获取符号的编码位长，构建符号位长表

2. 根据编码位长建立解码表。

3. 解码

注意：范式huffman编码有一个很重要的特性即长度为i的码字的前j位的数值大于长度为j的码字的数值，其中i > j。

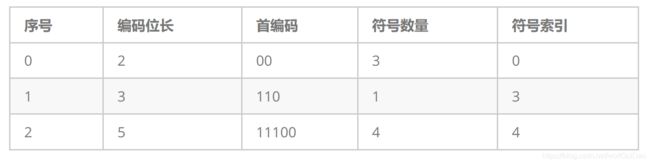
循环进行一下操作，直到所有的比特流解析完成：设i=0

1. 从解码表的第i行开始，根据编码位长从压缩数据比特流中获取相应长度的比特位。
2. 将读取的数据与首编码相减，假设结果为num
3. 如果num>=符号数量，i++，继续1，如果num小于符号数量，进行4
4. 将符号索引加上num，用该结果从符号位长表对应位置解析出该符号

例如，输入数据“11110”。令i = 0，此时编码位长为2。
				读取2位的数据“11”与首编码相减等于3。
3大于等于符号数量，于是i = i + 1等于1。此时编码位长为3。
				读取3位的数据“111”与首编码相减等于1。
1大于等于符号数量，于是i = i + 1等于2。此时编码位长为5。
				读取5位的数据“11110”与首编码相减等于2。
2小于符号数量，2加符号索引4等于6。
从表2.3中可以查到序号为6的符号是“E”。从而解码出符号“E”。
				跳过当前已经解码的5位数据，可以重新开始解码下一个符号。

4. Huffman压缩LZ77的结果

采用huffman树对LZ77的结果压缩时，GZIP将原字符和长度放在一起压缩，因为这两部分都占一个字节，将距离单独压缩。

4.1 距离的压缩

Z77在查找缓冲区中找匹配时，最长的距离不会超过32K，即最大的距离为32768，即距离的范围是[1,32768]，距离会非常多，虽然不会达到32768个，但是如果对于一个比较大的文件进行LZ编码，distance上千还是很正常的，因此会导致huffman树非常大，计算量和内存消耗都会超过当时的硬件条件，怎么办呢？

GZIP提供了一种非常好的方式，将distance划分成多个区间，每个区间当做一个整数来看，该整数称为Distance Code。当一个distance落到某个区间，则相当于出现了那个Code，虽然distance很多，Distance Code可以划分少一点，即多个distance对应一个Distance Code，最后只需要对Distance Code进行huffman编码即可。得到Code后，Distance Code再根据一定规则扩展出来。GZIP最终将distance划分成了30个区间，如下图：

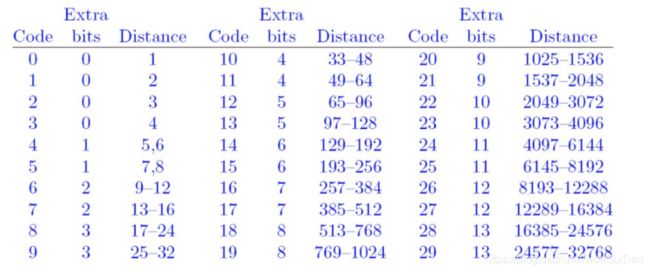
Code表示区间编号，[0,29]，总共是30个区间,每个区间容纳distance的个数刚好是2的n次幂，huffman树只对0~29这30个Code进行编码，

得到编码，Extra bits表示distance的编码需要再Code的编码基础上扩展的比特位个数，

比如：0表示不扩展，13表示要扩展13位，因为最大的区间中包含的distance数量为8192个。

比如：17~24这个区间的huffman编码为110，因为这个区间有8个整数，于是按照上述表格的规则就可以得到所有distance的编码：

17-----> 110 000
18-----> 110 001
19-----> 110 010
20-----> 110 011
21-----> 110 100
22-----> 110 101
23-----> 110 110
24-----> 110 111

这样就可以将树的高度降低，计算的时间和空间复杂度都降低了，而且扩展起来也比较简单

4.2 原字符和长度的压缩

原字符表示在LZ77中未匹配的字符，长度表示重复字符串的个数，都占了一个字节，因此GZIP将其压缩合二为一了，即对于原字符和距离采用同一棵huffman树进行处理。

原字符的范围是[0, 255]，距离是[3, 258]，如何进行处理呢？
GZIP用整数0~255表示原字符，256表示结束标志，即解码以后是256表示解码结束，从257开始表示距离，比如：257表示重复3个字符，258重复4个字符，但GZIP并没有一直这么一一对应，而是采用了和distance类似的方式进行分区，总共将距离划分成了29个区间，如下图

即原字符和距离的huffman编码的输入元素一共有285个，当解码器接收到一个比特流的时候，首先可以按 照literal/length这个码表来解码，如果解出来是0-255，就表示未匹配字符，如果是256，那自然就结束， 如果是257-285之间，则表示length，把后面扩展比特加上形成length后，后面的比特流肯定就表示 distance，

因此，实际上通过一个Huffman码表，对各类情况进行了统一，而不是通过加一个什么标志来 区分到底是literal还是重复字符串。

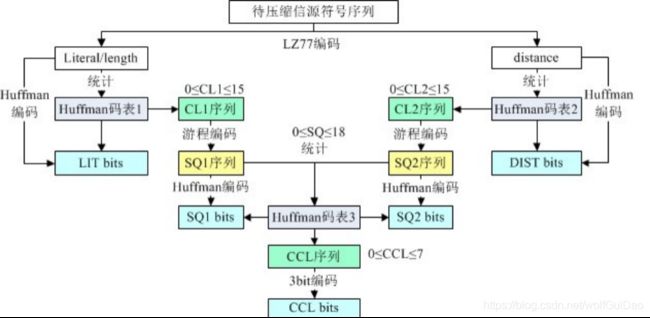
到此GZIP的主体压缩过程基本出来了，第一步：先是采用LZ77对源文件进行压缩，第二步采用huffman对 LZ77的压缩结果进行再次压缩，因为原字符和长度使用一棵huffman树，将其称为huffman码表1， distance对应huffman树称为huffman码表2，而最终的huffman树信息只需要使用码字长度保存即可，称之 为CL(Code Length)，即两个码表长度分别为：CL1、CL2。

码树记录下来，对原字符的编码比特流称为LIT比 特流，对distance编码的比特流称为DIST比特流。按照上面的方法，LZ的编码结果就变成四块：CL1、CL2、 LIT比特流、DIST比特流 。

5. CL的游程编码

编码的长度即CL也是一对数字，该部分信息理论也可以使用huffman树再次压缩，但是GZIP并没有对其使用huffman树进行压缩，而是使用了游程编码。

游程，即一段完全相同的数的序列。游程编码，即对一段连续相同的数，记录这个数一次，紧接着记录出现了多少个。比如CL序列如下：
4, 4, 4, 4, 4, 3, 3, 3, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 0, 0, 0, 0, 0, 0, 2, 2, 2, 2
那么，游程编码的结果为：

4, 16, 01（二进制）, 3, 3, 3, 6, 16, 11（二进制）, 16, 00（二进制）, 17,011（二进制）, 2, 16, 00（二进制）

这是什么意思呢？因为CL的范围是0-15，GZIP认为重复出现2次太短就不用游程编码了，所以游程长度从3开始。

用16这个特殊的数表示重复出现3、4、5、6个这样一个游程，分别后面跟着00、01、10、11表示（实际存储的时候需要低比特优先存储，需要把比特倒序来存，一些例子有时候会忽略这点，实际写程序的时候一定要注意，否则会得到错误结果）。

于是4,4,4,4,4,这段游程记录为4,16,01，也就是说，4这个数，后面还会连续出现了4次。6,16,11,16,00表示6后面还连续跟着6个6，再跟着3个6；

因为连续的0出现的可能很多，所以用17、18这两个特殊的数专门表示0游程，17后面跟着3个比特分别记录长度为3-10（总共8种可能）的游程；

18后面跟着7个比特表示11-138（总共128种可能）的游程。17,011（二进制）表示连续出现6个0；18,0111110（二进制）表示连续出现62个0。

总之记住，0-15是CL可能出现的值，16表示除了0以外的其它游程；17、18表示0游程。因为二进制实际上也是个整数，所以上面的序列用整数表示为：
4, 16, 1, 3, 3, 3, 6, 16, 3, 16, 0, 17, 3, 2, 16, 0

原字符和长度的编码符号总共有286个(256个原字符+1个结束标记+29个长度区间)，distance编码区间总共30个，因此这棵树不会特别深，huffman编码后的码字长度不会特别长，不会超过15，即树的深度不会超过15，因此CL1和CL2这两个序列的任意整数的值的范围是0-15,0表示没有出现，故GZIP对CL1和CL2使用了游程编码。

因为游程编码之后整数值的范围是0-18，这个序列称之为SQ，因为码字长度有CL1、CL2，因此最后有SQ1和SQ2两组数据。GZIP采用第三个huffman树对SQ1和SQ2再次进行huffman压缩。

通过统计各个整数（0-18范围内）的出现次数，按照相同的思路，对SQ1和SQ2进行了Huffman编码，得到的码流记为SQ1 bits和SQ2 bits。同时，这里又需要记录第三个码表，称为Huffman码表3。同理，这个码表也用相同的方法记录，也等效为一个码长序列，称为CCL。到此GZIP压缩才算真正结束，这个算法命名为Deflate算法：

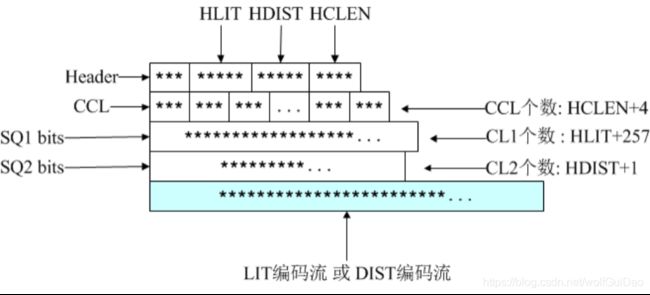
6. 数据存储格式

因为被压缩的文件可能非常大，会严重影响压缩率，因此GZIP采用了分段压缩处理，每段的压缩结果表示如 下：

总结：

1. 范式Huffman树是用来解决Huffman树当中字符频度信息、Huffman树太大的，用范式Huffman树当中每个字符的位长来代替Huffman树当中的字符频度，Huffman树当中每个字符的频度是[0，65535]，范式Huffman树的位长是[0，15]。
如可以采用...000000023456200000...共256个字节这样的方式来存储字符位长信息，多次重复出现的数字可以采用CL游程编码解决。这样就大大减少了标记信息所占用的空间，使用范式Huffman树，大大减少了遍历Huffman树的时间，提高压缩的效率。

2. 对于LZ77压缩的结果当中，有原字符也有长度距离信息，Huffman的压缩方法是把标记信息也压缩到Huffman树当中，那样是非常浪费空间的，范式Huffman树采用将distance划分成多个区间的方法，也在一定成程度上节省了空间

3. 范式Huffman树对原字符和长度的压缩是采用一起压缩的方法，因为二者都占一个字节，那么如何区分呢？因为一个字符的范围是[0,255],所以用来表示字符，用256来分割，[256，285]这29个区间来表示长度